图的存储结构分为邻接矩阵和邻接表两种,带权的图叫做网。
邻接矩阵
邻接矩阵适合边多的图
无向图
两个顶点之间的连线是双向的,一个一维数组存顶点,一个二维数组存边

若有边则值为1,反之为0

邻接矩阵需要知道点数、边数、一个二维数组存边、一个指针指向点,一个规定最多存放顶点数的值。
#define SIZE 10
class Graph
{
int m_MaxVertex;//最大顶点个数
int m_NumVertex;//实际顶点个数
int m_NumEdge;//边数
char* m_VertexArr;//存顶点
int m_Edge[SIZE][SIZE];//存边
public:
Graph();//构造
~Graph();//析构
void InsertVertex(char v);//插入点
void InsertEdge(char v1, char v2);//在点v1和v2之间插入边
void PrintGraph();//输出
int GetVertexIndex(char v);//获取下标
void DeleteEdge(char v1, char v2);//删除边
void DeleteVertex(char v);//删除点
};构造和析构函数
Graph::Graph()
{
m_MaxVertex = SIZE;//设置最大的顶点数
m_NumVertex = m_NumEdge = 0;//初始为0
for (int i = 0; i < m_MaxVertex; i++)
{
for (int j = 0; j < m_MaxVertex; j++)
m_Edge[i][j] = 0;
}
m_VertexArr = new char[m_MaxVertex];//m_VertexArr指向装顶点的数组
}
Graph::~Graph()
{
if (m_VertexArr != nullptr)
{
delete[]m_VertexArr;
m_VertexArr = nullptr;
}
m_NumEdge = m_NumVertex = 0;
}插入顶点
如果顶点数大于最多能存的顶点数,直接返回
否则存入存顶点的数组m_VertexArr,实际顶点数m_NumVertex++
//插入顶点
void Graph::InsertVertex(char v)
{
if (m_NumVertex >= m_MaxVertex)
{
return;
}
m_VertexArr[m_NumVertex++] = v;
}
得到一个顶点的下标
从第一个遍历到最后一个,若找到了,返回下标;若没找到,返回-1。
//得到下标
int Graph::GetVertexIndex(char v)
{
for (int i = 0; i < m_NumVertex; i++)
{
if (v == m_VertexArr[i])
{
return i;
}
}
return -1;
}插入边
在v1和v2两个顶点之间插入边:
首先找到两个顶点的下标;
若找到,使其存边数组中值等于1,因为是无向图,所以要m_Edge[p1][p2] = m_Edge[p2][p1]=1;
边数++
//插入边
void Graph::InsertEdge(char v1, char v2)
{
int p1 = GetVertexIndex(v1);
int p2 = GetVertexIndex(v2);
if (p1 == -1 || p2 == -1)return;
m_Edge[p1][p2] = m_Edge[p2][p1]=1;
m_NumEdge++;
}删除边
与插入边类似。
//删边
void Graph::DeleteEdge(char v1, char v2)
{
int p1 = GetVertexIndex(v1);
int p2 = GetVertexIndex(v2);
if (p1 == -1 || p2 == -1)return;
m_Edge[p1][p2] = m_Edge[p2][p1] = 0;
m_NumEdge--;
}删除点
方法1:直接删
这个方法比较麻烦,要将点、边数组中该点后面的数据全部往前移,如果边多不适合该方法
1.找下标,2.求相连边数,3.删点,4.删边行列(出、入)
void Graph::DeleteVertex(char v)
{
int p = GetVertexIndex(v);//找点下标
if (p == -1)return;
int i = 0,j = 0;
int delEdge = 0;//删除边的个数
for (i = 0; i < m_NumVertex; i++)//计算与该点相连的边的个数
{
if (m_Edge[p][i] = 1)
delEdge++;
}
for (i = p; i < m_NumVertex-1; i++)
{
m_VertexArr[i] = m_VertexArr[i + 1];//删顶点(把数组中后面的点往前移)
}
for (i = p; i < m_NumVertex-1; i++)
{
for (j = 0; j < m_NumVertex; j++)
{
m_Edge[j][i] = m_Edge[j][i + 1];//删列
}
}
for (i = p; i < m_NumVertex - 1; i++)
{
for (j = 0; j < m_NumVertex - 1; j++)
{
m_Edge[i][j] = m_Edge[i + 1][j];//删行
}
}
m_NumEdge -= delEdge;//更新边数
m_NumVertex--;//更新点数
}方法2:替换法
用最后一个顶点替换要删除的顶点,边用最后一行替换要删的,这样数组大小直接--就可删。
void Graph::DeleteVertex(char v)
{
int p = GetVertexIndex(v);//找下标
if (p == -1)return;
int i = 0, j = 0;
int delEdge = 0;//删除的边数
for (i = 0; i < m_NumVertex; i++)//求相连的边数
{
if (m_Edge[p][i] = 1)
delEdge++;
}
m_VertexArr[p] = m_VertexArr[m_NumVertex - 1];//要删的点替换成数组中最后一个点
for (i = 0; i < m_NumVertex; i++)
{
m_Edge[i][p] = m_Edge[i][m_NumVertex - 1];//要删的边替换成数组中最后列边
}
for (i = 0; i < m_NumVertex - 1; i++)//注意这里点数-1
{
m_Edge[p][i] = m_Edge[m_NumVertex - 1][i];//要删的边替换成数组中最后行边
}
m_NumEdge -= delEdge;//更新边
m_NumVertex--;//更新点
}
输出
void Graph::PrintGraph()
{
int i, j;
cout << " ";
for (i = 0; i < m_NumVertex; i++)
{
cout << m_VertexArr[i] << " ";//A B C D
}
cout << endl;
for (i = 0; i < m_NumVertex; i++)
{
cout << m_VertexArr[i] << " ";//竖行的ABCD
for (j = 0; j < m_NumVertex; j++)
{
cout << m_Edge[i][j] << " ";//输出边
}
cout << endl;
}
}测试
int main()
{
Graph g;
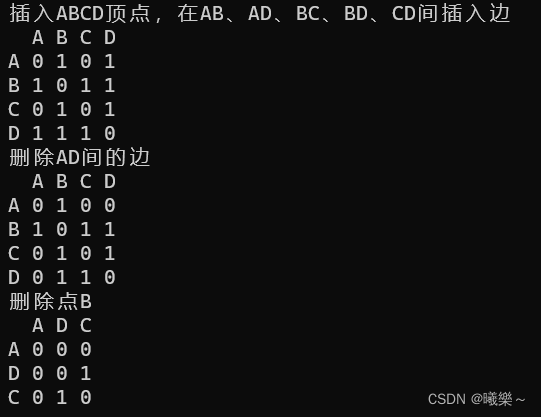
cout << "插入ABCD顶点,在AB、AD、BC、BD、CD间插入边\n";
g.InsertVertex('A');
g.InsertVertex('B');
g.InsertVertex('C');
g.InsertVertex('D');
g.InsertEdge('A', 'B');
g.InsertEdge('A', 'D');
g.InsertEdge('B', 'C');
g.InsertEdge('B', 'D');
g.InsertEdge('C', 'D');
g.PrintGraph();
cout << "删除AD间的边\n";
g.DeleteEdge('A', 'D');
g.PrintGraph();
cout << "删除点B\n";
g.DeleteVertex('B');
g.PrintGraph();
}
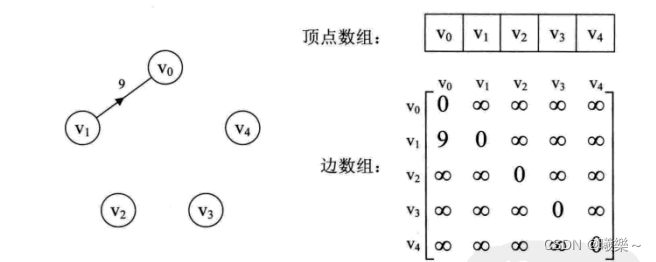
网的邻接矩阵中无边的为正无穷符号,可以用INT_MAX表示,其他的边数组的值为权值