一、快速排序

时间复杂度：

平均情况O(nlog2n)

最坏情况O(n^2)

思路

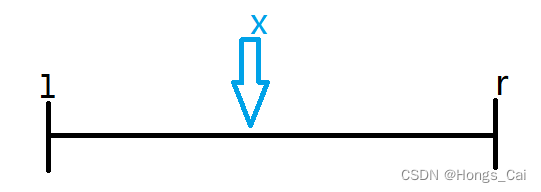
1. 确定分界点x (可取为q[l]、q[r]或 q[(l + r) / 2])

【x被称为支点（pivot），也称为枢轴元素。】

2. 划分区间 ( 将区间[l, r]划分为 <= x 和 >= x )【重点】

3. 利用递归把小于基准值元素的子数列和大于基准值元素的子数列进行排序

动画演示

模板

void quick_sort(vector<int>& q, int l, int r)
{
	if (l >= r) return;
	int x = q[(r + l) >> 1], i = l - 1, j = r + 1;
	while (i < j)
	{
		do i++; while (q[i] < x);
		do j--; while (q[j] > x);
		if (i < j) std::swap(q[i], q[j]);
	}
	quick_sort(q, l, j);
	quick_sort(q, j + 1, r);
}

注意点

【注意边界问题】

取左端点或右端点作为支点元素的方法比较简单，但是在某些情况下可能会导致快速排序算法出现最坏情况。

例如待排序数组已经有序或者接近有序的情况下。在这种情况下，取左端点或右端点作为支点元素会导致分割出来的左右两个子数组极度不平衡，导致算法效率变得极低。

取中间点作为支点元素的方法可以避免快速排序算法出现最坏情况，但是需要额外的计算来确定中间点的位置，可能会导致效率降低。因此，一般来说，随机选择法或三数取中法更常用，它们都可以避免最坏情况的发生，同时具有较高的效率和良好的性能。

切忌将 q[i] < x 改为 q[i] <= x 或是将 q[j] > x 改为 q[j] >= x ，会导致满足条件的数组下，指针无限移动，无限循环。

当支点选择q[l]时，递归填入区间必须为[l, j]和[j + 1, r]；当支点选择q[r]时，递归递归填入区间必须为[l, i]和[i + 1, r]，否则会触发边界问题。

二、归并排序

时间复杂度：O(nlog2n)

思路

1. 确定分界点

2. 递归排序

3. 归并（合二为一）【重点】

动画演示

在这里插入图片描述

模板

const int N = 1000;
vector<int> tmp(N);
void merge_sort(vector<int>& q, int l, int r)
{
	if (l >= r) return;
	int mid = (l + r) >> 1;
	merge_sort(q, l, mid);
	merge_sort(q, mid + 1, r);
	int i = l, j = mid + 1, k = 0;
	while (i <= mid && j <= r)
		if (q[i] <= q[j]) tmp[k++] = q[i++];
		else tmp[k++] = q[j++];
	while (i <= mid) tmp[k++] = q[i++];
	while (j <= r) tmp[k++] = q[j++];
	
	for (i = l, j = 0; i <= r; ++i, ++j) q[i] = tmp[j];
}

注意点

确定归并排序的边界条件：在实现归并排序时，需要确定递归终止的边界条件，一般是当待排序数组的大小小于等于1时，直接返回即可。

数组下标越界问题：在归并排序中，需要使用一个临时数组来存储排序结果，如果临时数组的大小不够或者在操作数组时下标越界，会导致程序出错。

归并排序的稳定性：归并排序是一种稳定的排序算法，即排序后相同元素的相对位置不变。在实现归并排序时，需要注意保持排序的稳定性。

归并排序的时间和空间复杂度：归并排序的时间复杂度为O(nlogn)，空间复杂度为O(n)，在排序大规模数据时，可能会出现内存溢出等问题，需要注意。

优化归并排序：归并排序虽然时间复杂度很好，但是在实际应用中可能会出现一些效率问题。可以通过一些优化措施来提高归并排序的效率，例如使用循环代替递归、使用插入排序优化小数组的排序等。

三、习题

1.第k个数

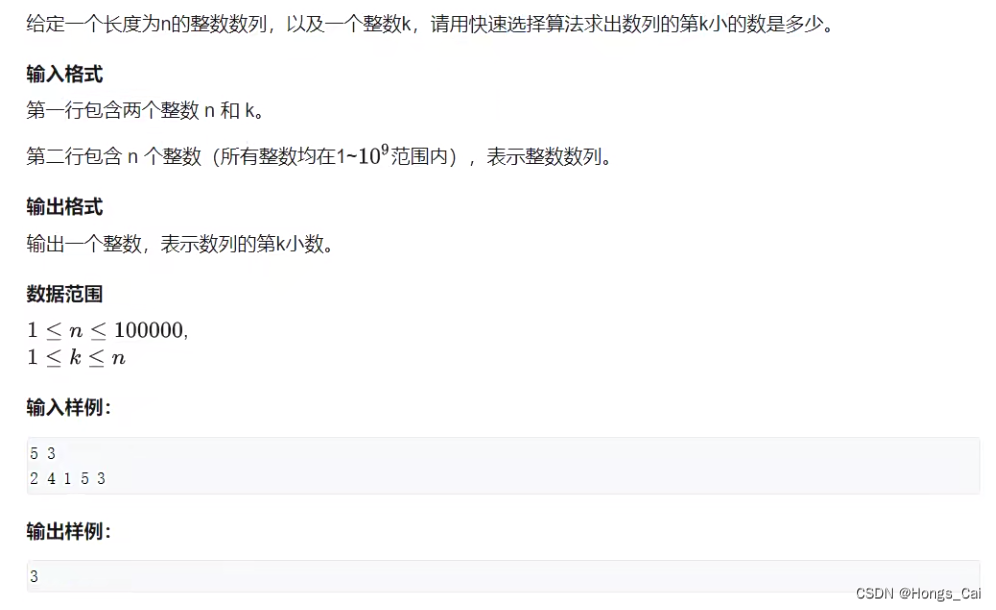
支点选择出来后，选择递归的范围。

当k <= i，递归左区间 [l, i]。

当k >= j，递归右区间 [j, r]。

时间复杂度：

n + n / 2 + n / 4 + ... <= 2n
O(n)

#include<iostream>

class solution
{
public:
	int quick_sort(int q[], int l, int r, int k)
	{
		if (l >= r) return q[l];
		int x = q[(l + r) >> 1], i = l - 1, j = r + 1;
		while (i < j)
		{
			do i++; while (q[i] < x);
			do j--; while (q[j] > x);
			if (i < j) std::swap(q[i], q[j]);
		}
		if (k <= j) return quick_sort(q, l, j, k);
		return quick_sort(q, j + 1, r, k);
	}
};
int main()
{
    const int N = 1000;
	int q[N];
	int n, k;
	scanf("%d%d", &n, &k);

	for (int i = 0; i < n; i++) scanf("%d", &q[i]);

	std::cout << solution().quick_sort(q, 0, n - 1, k - 1) << std::endl;
    // 传入（k - 1）来指向第k小目标的坐标

    return 0;
}

2.数组中的逆序对*

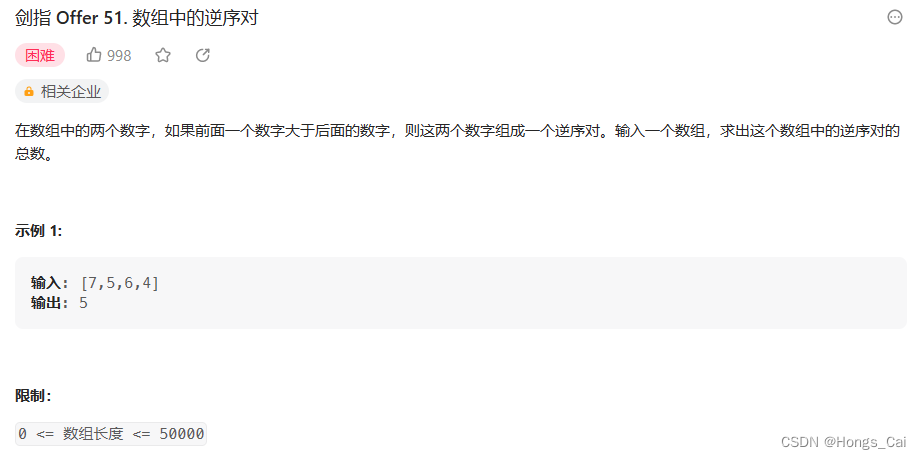
利用数组局部有序性，在归并过程中利用两指针之差来计算出对应的逆序数。

class Solution {
public:
	int reversePairs(vector<int>& nums)
	{
		int tmp[nums.size()];
		return merge_sort(nums, tmp, 0, nums.size() - 1);
	}
private:
	long merge_sort(vector<int>& q, int tmp[], int l, int r)
	{
		if (l >= r) return 0;
		int mid = (l + r) >> 1;
		long long res = merge_sort(q, tmp, l, mid) + merge_sort(q, tmp, mid + 1, r);

		int k = 0, i = l, j = mid + 1;
		while (i <= mid && j <= r)
			if (q[i] <= q[j]) tmp[k++] = q[i++];
			else
			{
				res += (mid + 1 - i);
				tmp[k++] = q[j++];
			}
		while (i <= mid) tmp[k++] = q[i++];
		while (j <= r) tmp[k++] = q[j++];
		
		for (i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
		return res;
	}
};