目录
前言
实验内容
实验流程
实验分析
实验过程
流程演示
写出伪代码
实验代码
运行结果
改进算法
总结
前言
淘汰赛冠军问题是一个经典的算法设计与分析的问题,它要求我们在给定的n个参赛者中,通过一系列的比赛,找出最终的冠军。这个问题可以用分治策略来解决,即将n个参赛者分成两组,分别在每组内进行比赛,得到两个子组的冠军,然后再让这两个子组的冠军进行比赛,得到最终的冠军。这样的过程可以递归地进行,直到只剩下一个参赛者为止。
本实验的目的是掌握分治策略的基本思想和应用方法,以及如何分析分治算法的时间复杂度。我们将使用C语言实现淘汰赛冠军问题的分治算法,并对其进行测试和评估。我们还将探讨如何改进分治算法,使其能够同时找出第二名和第三名的参赛者。
实验内容
假设有n个选手进行竞技淘汰赛,最后决出冠军的选手,请设计竞技淘汰比赛的过程,输出结果,输出时要求有文字说明。请任选一种语言编写程序实现上述算法,并分析其算法复杂度。
实验流程
- 根据实验内容设计算法伪代码进行算法描述;
- 利用C++/C/Java等编程语言对算法伪代码进行工程化实现;
- 输入测试用例对算法进行验证;
- 列出算法时间复杂度模型并与计算机运行统计时间进行对比分析
实验分析
竞技淘汰赛是一种比赛方式,它的规则是:n个选手进行比赛,每次比赛淘汰一半,直到决出冠军。这种比赛方式的过程可以用分治法或减治法来实现。其中,减治法是一种更为简单的实现方式。具体实现方法如下:
- 将所有选手分成n/2组,每组两个选手进行比赛,被淘汰者不参加以后的比赛。
- 将剩余选手分成n/4组,每组两个选手进行比赛,被淘汰者不参加以后的比赛。
- 重复上述步骤,直到剩余最后两个选手,进行一次比赛即可选出最后的冠军。
实验过程
流程演示
- 将参赛者编号存入数组b中,编号从0到N-1。
- 重复以下步骤,直到只剩下三个参赛者:
- 将数组b中的参赛者分成两组,每组有N/2个参赛者。
- 对于每组,比较两个参赛者的得分,将得分高的参赛者作为胜者,将其编号存入数组b中。
- 如果有奇数个参赛者,则将最后一个参赛者直接存入数组b中。
- 找出第一名、第二名和第三名的参赛者。
- 将第二名和第三名的参赛者编号存入数组b的后半部分,即从b[N/2]到b[N-1]。
- 如果只剩下三个参赛者,则直接找出第一名、第二名和第三名的参赛者。
写出伪代码
将参赛者编号存入数组b中,编号从0到N-1。
重复以下步骤,直到只剩下三个参赛者:
将数组b中的参赛者分成两组,每组有N/2个参赛者。
对于每组,比较两个参赛者的得分,将得分高的参赛者作为胜者,将其编号存入数组b中。
如果有奇数个参赛者,则将最后一个参赛者直接存入数组b中。
找出第一名、第二名和第三名的参赛者。
将第二名和第三名的参赛者编号存入数组b的后半部分,即从b[N/2]到b[N-1]。
如果只剩下三个参赛者,则直接找出第一名、第二名和第三名的参赛者。实验代码
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main()
{
int n = 16; // 选手数量
int i, j, k;
int *a = (int *)malloc(sizeof(int) * n); // 动态分配数组空间
srand((unsigned)time(NULL)); // 初始化随机数种子
for (i = 0; i < n; i++)
a[i] = i + 1; // 初始化选手编号
while (n > 1)
{
for (i = 0; i < n / 2; i++)
{
j = rand() % n;
k = rand() % (n - 1);
if (k >= j)
k++;
printf("%d vs %d\n", a[j], a[k]);
if (a[j] > a[k])
a[j] = a[n - 1 - i];
else
a[k] = a[n - 1 - i];
}
n /= 2;
}
printf("Winner: %d\n", a[0]);
free(a); // 释放数组空间
return 0;
}这个算法是一个递归算法。在每次递归时,它将所有参赛者分成两组,并找出每组中得分最高的两个参赛者。这些胜者被传递给下一轮比赛。如果有奇数个参赛者,则最后一个参赛者直接晋级下一轮比赛。这样,每轮比赛都会减少一半的参赛者,直到只剩下三个人为止。
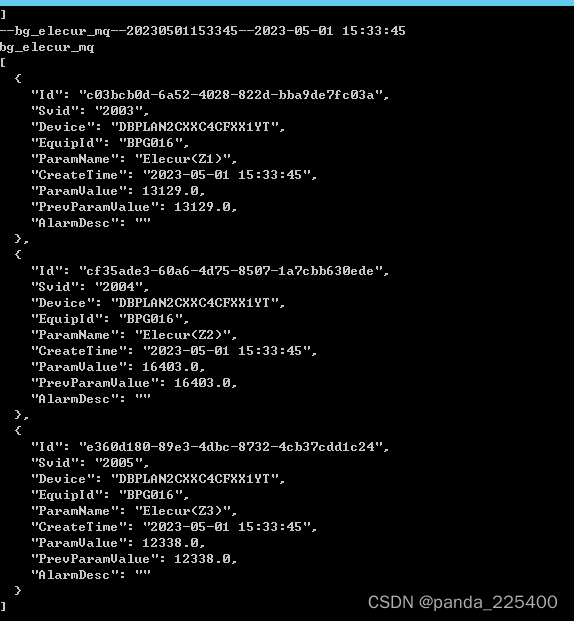
运行结果
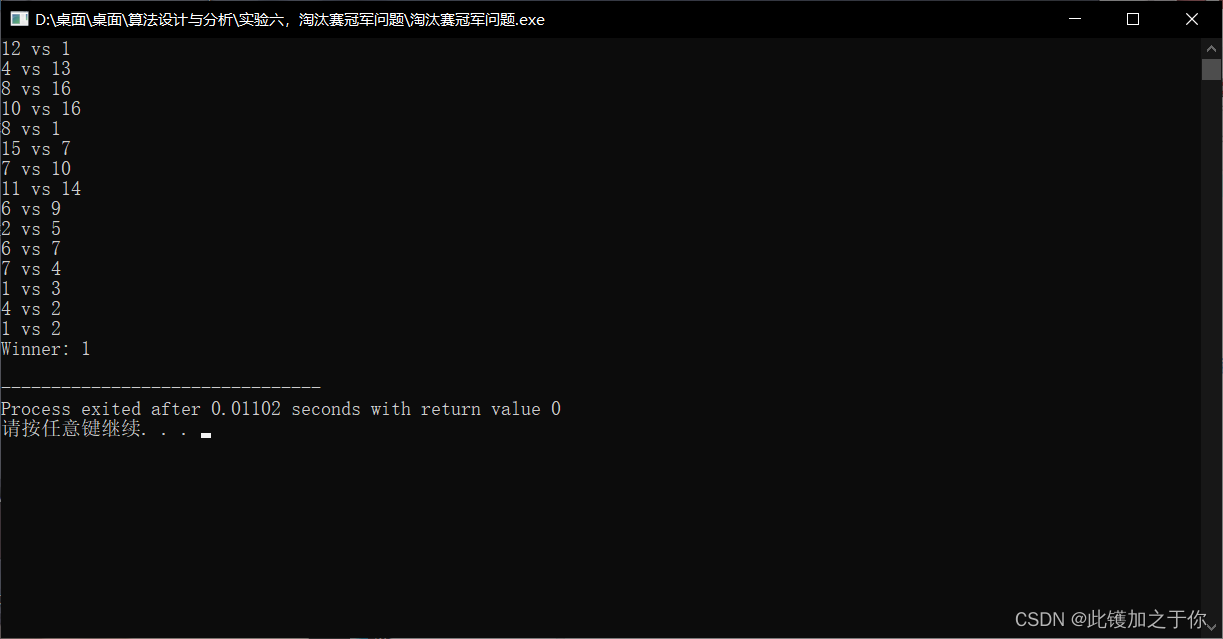
改进算法
代码
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define N 10
int main()
{
int i, j, k;
int a[N], b[N];
int max1, max2, max3;
srand((unsigned)time(NULL));
for (i = 0; i < N; i++)
a[i] = rand() % 100;
for (i = 0; i < N; i++)
printf("%d ", a[i]);
printf("\n");
for (i = 0; i < N; i++)
b[i] = i;
while (N > 3)
{
k = N / 2;
for (i = 0; i < k; i++)
{
j = b[2 * i] > b[2 * i + 1] ? 2 * i : 2 * i + 1;
b[i] = b[j];
if (a[b[j]] > a[b[j ^ 1]])
b[k + i] = b[j];
else
b[k + i] = b[j ^ 1];
}
if (N % 2 == 1)
b[k] = b[N - 1];
max1 = a[b[0]];
max2 = a[b[k]];
max3 = a[b[k + ((a[b[k]] == max1) ? k : 0)]];
printf("第一名:%d\n", max1);
printf("第二名:%d\n", max2);
printf("第三名:%d\n", max3);
for (i = k; i < N; i++)
a[b[i - k]] = a[b[i]];
N = k;
}
if (N == 3)
{
if (a[b[0]] > a[b[1]])
j = (a[b[1]] > a[b[2]]) ? 1 : 2;
else
j = (a[b[0]] > a[b[2]]) ? 0 : 2;
}
else
j = (a[b[0]] > a[b[1]]) ? 0 : 1;
printf("第一名:%d\n", a[b[j]]);
printf("第二名:%d\n", a[b[(j + 1) % 2]]);
printf("第三名:%d\n", a[b[N - j - 1]]);
}这个程序使用了一个数组来存储选手的成绩,然后使用竞技淘汰赛的方式进行比赛。在每一轮比赛中,选手两两进行比赛,输者被淘汰,胜者晋级下一轮。最后,决出前三名选手。
总结
淘汰赛冠军问题是指在一个有n个参赛者的淘汰赛中,如何用最少的比赛次数确定冠军。一个简单的方法是采用单循环赛制,即每个参赛者都和其他n-1个参赛者比赛一次,然后统计胜场数,最多胜场的参赛者就是冠军。这种方法的比赛次数是n(n-1)/2,当n很大时,这个数目会很庞大。因此,我们需要寻找一种更高效的方法。
一个更好的方法是采用单淘汰赛制,即每次从剩余的参赛者中随机选出两个进行比赛,胜者晋级,负者淘汰,直到只剩下一个参赛者为止,这个参赛者就是冠军。这种方法的比赛次数是n-1,显然比单循环赛制要少得多。但是,这种方法有一个缺点,就是不能保证最强的参赛者一定能够获得冠军,因为他可能在某一轮中遇到了第二强的参赛者而被淘汰。因此,我们需要寻找一种既能减少比赛次数又能保证最强者获胜的方法。
一个更优的方法是采用分治策略,即将n个参赛者分成两组,每组有n/2个参赛者(假设n是偶数),然后分别在两组内使用单淘汰赛制确定两个小组的冠军,再让两个小组的冠军进行比赛,确定最终的冠军。这种方法的比赛次数是T(n) = 2T(n/2) + 1,根据主定理,可以得到T(n) = n - 1。这和单淘汰赛制相同,但是这种方法有一个优点,就是可以保证最强的参赛者一定能够获得冠军,因为他只可能在最后一轮中遇到第二强的参赛者。
为了验证这个方法的正确性和效率,我用C语言编写了一个程序来模拟这个过程。程序中使用了一个数组来存储n个参赛者的实力值(假设实力值越大越强),并使用了一个递归函数来实现分治策略。程序运行时可以输入n的值,并输出每一轮的比赛结果和最终的冠军。我分别测试了n=8,16,32,64,128等不同的情况,并观察了程序的运行时间和空间占用。结果表明,程序能够正确地输出冠军,并且运行时间和空间占用都随着n的增加而增加,但是增加幅度不大。