例题来源：侯忠生教授的《无模型自适应控制：理论与应用》（2013年科学出版社）。

👉对应书本 4.3 单输入单输出系统(SISO)偏格式动态线性化(PFDL)的无模型自适应控制(MFAC)

上一篇博客介绍了基于紧格式动态线性化的无模型自适应控制。
【Matlab】基于紧格式动态线性化的无模型自适应控制
紧格式动态线性化(CFDL)与偏格式动态线性化(PFDL)的格式类似，但偏格式动态线性化(PFDL)多了一个控制变量，线性化长度由1变成L.

例题4.4

1.题目要求

在CFDL中，线性化长度常数 L=1，步长因子仅有1个($\rho$)，伪偏导数(PPD) ${\varphi }_c$ 是一个数，而在PFDL中，PPD ${\varphi }_{p,L}$ 是一个 L 维的向量，步长因子增多(${\rho }_1,{\rho }_2,...,{\rho }_{L_y}$)。

2.matlab代码

clear all; clc;

%% 控制器参数
L=3; % 输入阶数
eta=0.5; % 伪偏导步长
miu=1; % 伪偏导权重
rho=0.5; % 控制律步长 rho1=rho2=rho3=0.5
lamda=0.01; % 控制律权重
epsilon=1e-5; % 伪偏导重置阈值
N=400; %采样时间

%% 初值
y(1:6)=0; y(4)=1;
u(1:5)=0;
du(1:5,1:L)=0;

%% 期望值
for k=1:N+1
    yd(k)=5*(-1)^round(k/80);
end
figure(1)
plot(yd,'k');
hold on;

%% 控制器伪偏导数初值
% phi_{p,L}(k) = [phi_1(k), phi_2(k),...,phi_L(k)]^T
% phi(k,i):第1个参数是k(1~N)，第2个参数是i(1~L)
phi(1:5,1)=1;
phi(1:5,2:L)=0;

for k=6:N
    %% 伪偏导更新
    % Delta{U_L(k)} = [Delta{u(k)}, Delta{u(k-1)},...,Delta{u(k-(L-1))}]^T
    % du(k,i):第1个参数是k(1~N)，第2个参数是i(1~L)
    phi(k,1:L)=phi(k-1,1:L)+eta*(y(k)-y(k-1)-phi(k-1,1:L)*du(k-1,1:L)')*du(k-1,1:L)/(miu+du(k-1,1:L)*du(k-1,1:L)');
    % 伪偏导重置
    if abs(phi(k,1))<=epsilon | abs(du(k-1, 1:L))<= epsilon | sign(phi(k,1))~=sign(phi(1,1))
        phi(k,1)=0.5;
    end
    
    %% 控制律更新
    if L==1
        u(k) = u(k-1)+rho*phi(k,1)*(yd(k+1)-y(k))/(lamda+phi(k,1).^2);       
    else
        u(k) = u(k-1)+rho*phi(k,1)*(yd(k+1)-y(k)-phi(k,2:L)*du(k-1,1:L-1)')/(lamda+phi(k,1).^2); 
    end
    
    %% 系统函数
    if k<=200
        y(k+1)=2.5*y(k)*y(k-1)/(1+y(k).^2+y(k-1).^2)+0.7*sin(0.5*(y(k)+y(k-1)))+1.4*u(k-1)+1.2*u(k);
    else
        y(k+1)=-0.1*y(k)-0.2*y(k-1)-0.3*y(k-2)+0.1*u(k)+0.02*u(k-1)+0.03*u(k-2);    
    end
    
    for i=1:L
        du(k,i)=u(k-i+1)-u(k-i);
    end
    error(k+1)=yd(k+1)-y(k+1);
end

%% 画图
figure(1)
plot(y,'--r');
xlim([0 400]); ylim([-15 15]);
xlabel('time'); ylabel('tracking performance');
legend('y*(k)', 'PFDL-MFAC');
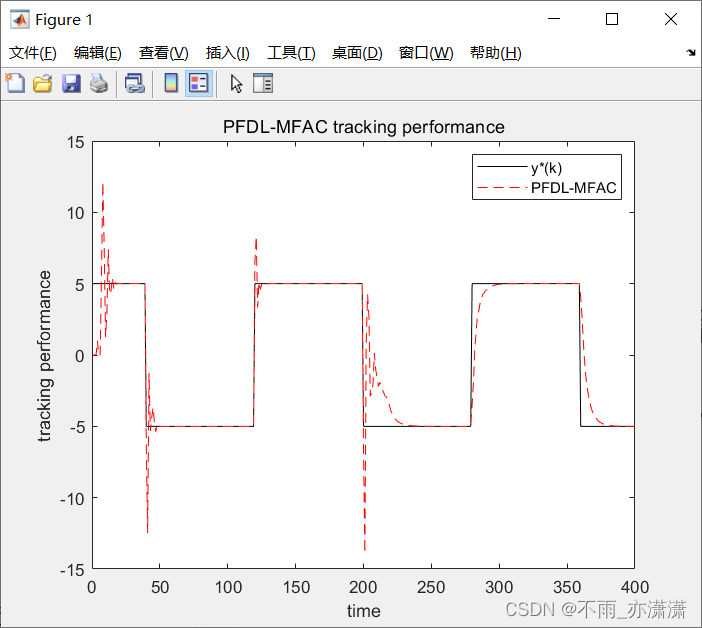
title('PFDL-MFAC tracking performance');

figure(2)
plot(u,'b');
ylim([-60 60]);
xlabel('time'); ylabel('input');
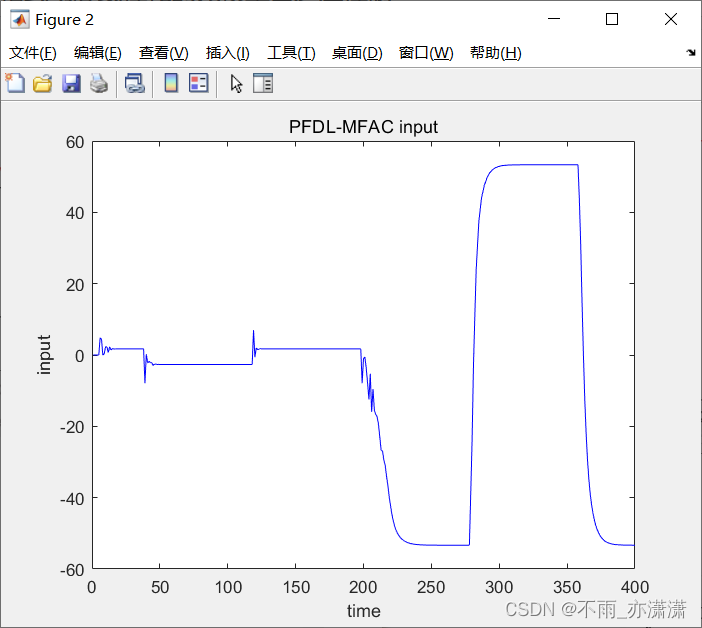
title('PFDL-MFAC input');

figure(3)
plot(phi(:,1),'b--');hold on;
plot(phi(:,2),'r--');hold on;
plot(phi(:,3),'g--');
xlabel('time'); ylabel('PPD');
legend('\phi_1(k)','\phi_2(k)','\phi_3(k)');
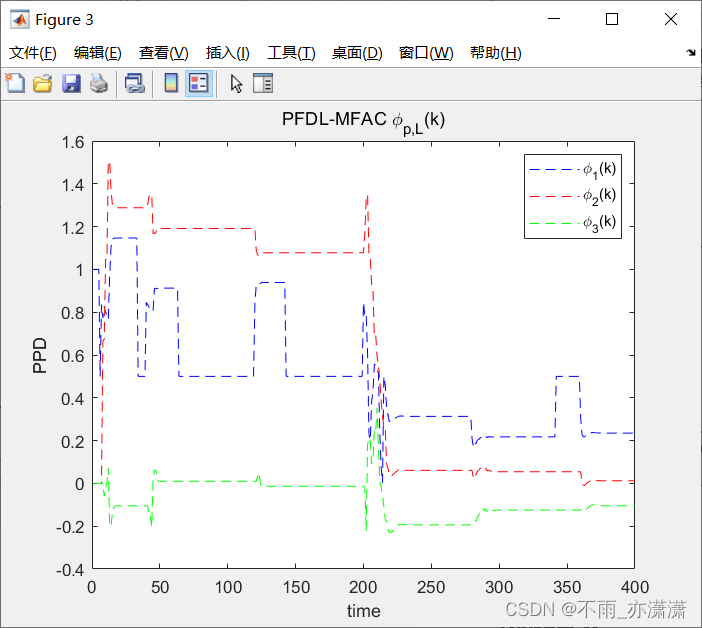
title('PFDL-MFAC \phi_{p,L}(k)');

figure(4)
plot(error);
xlabel('time'); ylabel('tracking error');
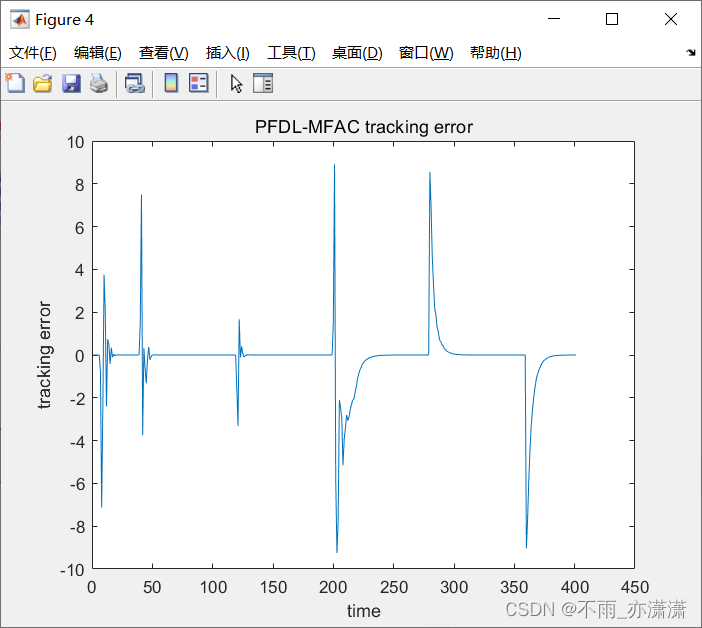
title('PFDL-MFAC tracking error')

3.运行结果

跟踪性能

控制输入

PPD估计

跟踪误差

例题4.5

1.题目要求

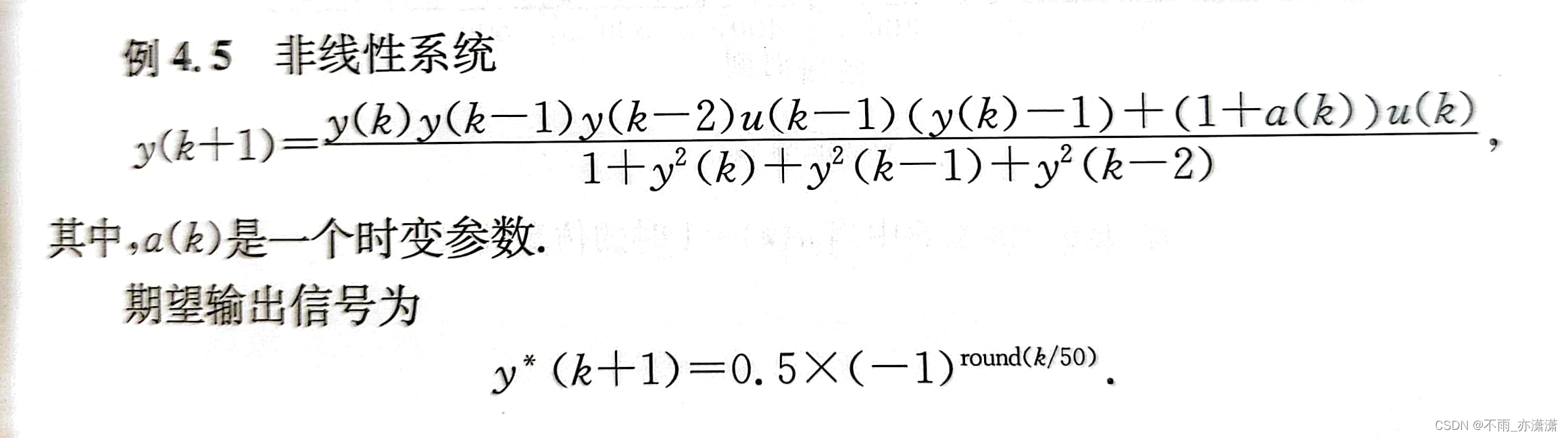
取 a(k)=1

2.matlab代码

clear all; clc;

%% 控制器参数
L=3; % 输入阶数
eta=0.5; % 伪偏导步长
miu=1; % 伪偏导权重
rho=0.5; % 控制律步长 rho1=rho2=rho3=0.5
lamda=0.01; % 控制律权重
epsilon=1e-5; % 伪偏导重置阈值
N=800; %采样时间

%% 初值
y(1:6)=0; y(4)=1;
u(1:5)=0;
du(1:5,1:L)=0;

%% 期望值
for k=1:N+1
    yd(k)=0.5*(-1)^round(k/50);
end
figure(1)
plot(yd,'k');
hold on;

%% 控制器伪偏导数初值
% phi_{p,L}(k) = [phi_1(k), phi_2(k),...,phi_L(k)]^T
% phi(k,i):第1个参数是k(1~N)，第2个参数是i(1~L)
phi(1:5,1)=1;
phi(1:5,2:L)=0;

for k=6:N
    %% 伪偏导更新
    % Delta{U_L(k)} = [Delta{u(k)}, Delta{u(k-1)},...,Delta{u(k-(L-1))}]^T
    % du(k,i):第1个参数是k(1~N)，第2个参数是i(1~L)
    phi(k,1:L)=phi(k-1,1:L)+eta*(y(k)-y(k-1)-phi(k-1,1:L)*du(k-1,1:L)')*du(k-1,1:L)/(miu+du(k-1,1:L)*du(k-1,1:L)');
    % 伪偏导重置
    if abs(phi(k,1))<=epsilon | abs(du(k-1, 1:L))<= epsilon | sign(phi(k,1))~=sign(phi(1,1))
        phi(k,1)=0.5;
    end
    
    %% 控制律更新
    if L==1
        u(k) = u(k-1)+rho*phi(k,1)*(yd(k+1)-y(k))/(lamda+phi(k,1).^2);       
    else
        u(k) = u(k-1)+rho*phi(k,1)*(yd(k+1)-y(k)-phi(k,2:L)*du(k-1,1:L-1)')/(lamda+phi(k,1).^2); 
    end
    
    %% 系统函数
    y(k+1)=(y(k)*y(k-1)*y(k-2)*u(k-1)*(y(k)-1)+(1+1)*u(k)) / (1+y(k)^2+y(k-1)^2+y(k-2)^2);
    
    for i=1:L
        du(k,i)=u(k-i+1)-u(k-i);
    end
    error(k+1)=yd(k+1)-y(k+1);
end

%% 画图
plot(y,'--r');
xlim([0 800]); 
xlabel('time'); ylabel('tracking performance');
legend('y*(k)', 'PFDL-MFAC');
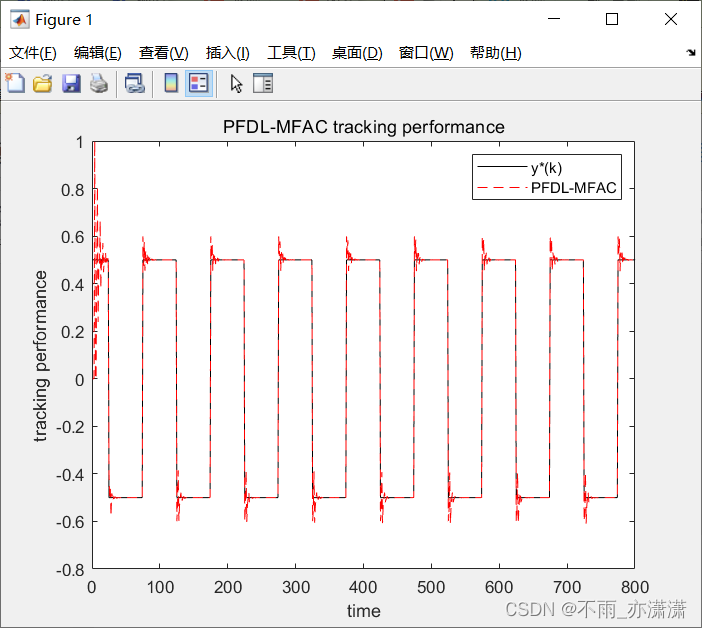
title('PFDL-MFAC tracking performance');

3.运行结果