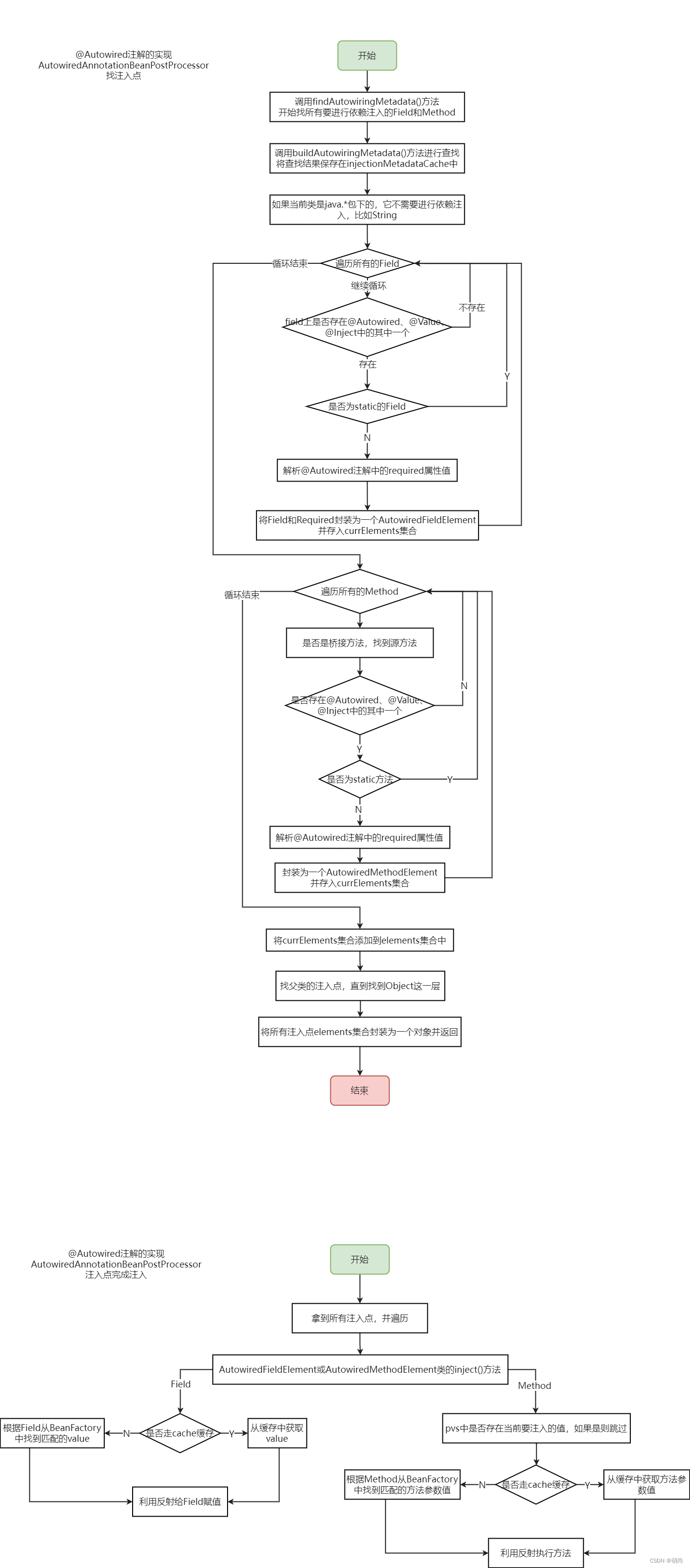
Cont.
举例
例1
词频 (TF) 是一词语出现的次数除以该文件的总词语数。
假如一篇文件的总词语数是100个,而词语“母牛”出现了3次,那么“母牛”一词在该文件中的词频就是3/100=0.03。
一个计算文件频率 (IDF) 的方法是文件集里包含的文件总数除以测定有多少份文件出现过“母牛”一词。
所以,如果“母牛”一词在1,000份文件出现过,而文件总数是10,000,000份的话,其逆向文件频率就是 lg(10,000,000 / 1,000)=4。
最后的TF-IDF的分数为0.03 * 4=0.12。
例2
在某个一共有一千词的网页中“原子能”、“的”和“应用”分别出现了 2 次、35 次 和 5 次,那么它们的词频就分别是 0.002、0.035 和 0.005。
我们将这三个数相加,其和 0.042 就是相应网页和查询“原子能的应用” 相关性的一个简单的度量。
概括地讲,如果一个查询包含关键词 w1,w2,…,wN, 它们在一篇特定网页中的词频分别是: TF1, TF2, …, TFN。 (TF: term frequency)。
那么,这个查询和该网页的相关性就是:TF1 + TF2 + … + TFN。
漏洞
在上面的例子中,词“的”占了总词频的 80% 以上,而它对确定网页的主题几乎没有用。我们称这种词叫“应删除词”(Stopwords),也就是说在度量相关性是不应考虑它们的频率。在汉语中,应删除词还有“是”、“和”、“中”、“地”、“得”等等几十个。忽略这些应删除词后,上述网页的相似度就变成了0.007,其中“原子能”贡献了 0.002,“应用”贡献了 0.005。细心的读者可能还会发现另一个小的漏洞。在汉语中,“应用”是个很通用的词,而“原子能”是个很专业的词,后者在相关性排名中比前者重要。因此我们需要给汉语中的每一个词给一个权重,这个权重的设定必须满足下面两个条件:
- 一个词预测主题能力越强,权重就越大,反之,权重就越小。我们在网页中看到“原子能”这个词,或多或少地能了解网页的主题。我们看到“应用”一次,对主题基本上还是一无所知。因此,“原子能“的权重就应该比应用大。
- 应删除词的权重应该是零。
我们很容易发现,如果一个关键词只在很少的网页中出现,我们通过它就容易锁定搜索目标,它的权重也就应该大。反之如果一个词在大量网页中出现,我们看到它仍然不是很清楚要找什么内容,因此它应该小。概括地讲,假定一个关键词 w 在 Dw 个网页中出现过,那么 Dw 越大,w的权重越小,反之亦然。在信息检索中,使用最多的权重是“逆文本频率指数” (Inverse document frequency 缩写为IDF),它的公式为log(D/Dw)其中D是全部网页数。比如,我们假定中文网页数是D=10亿,应删除词“的”在所有的网页中都出现,即Dw=10亿,那么它的IDF=log(10亿/10亿)= log (1) = 0。假如专用词“原子能”在两百万个网页中出现,即Dw=200万,则它的权重IDF=log(500) =2.7。又假定通用词“应用”,出现在五亿个网页中,它的权重IDF = log(2)则只有 0.3。也就是说,在网页中找到一个“原子能”的匹配相当于找到九个“应用”的匹配。利用 IDF,上述相关性计算的公式就由词频的简单求和变成了加权求和,即 TF1IDF1 + TF2IDF2 +… + TFN*IDFN。在上面的例子中,该网页和“原子能的应用”的相关性为 0.0069,其中“原子能”贡献了 0.0054,而“应用”只贡献了0.0015。这个比例和我们的直觉比较一致了。
应用
权重计算方法经常会和余弦相似度(cosine similarity)一同使用于向量空间模型中,用以判断两份文件之间的相似性。
理论假设
TFIDF算法是建立在这样一个假设之上的:对区别文档最有意义的词语应该是那些在文档中出现频率高,而在整个文档集合的其他文档中出现频率少的词语,所以如果特征空间坐标系取TF词频作为测度,就可以体现同类文本的特点。另外考虑到单词区别不同类别的能力,TFIDF法认为一个单词出现的文本频数越小,它区别不同类别文本的能力就越大。因此引入了逆文本频度IDF的概念,以TF和IDF的乘积作为特征空间坐标系的取值测度,并用它完成对权值TF的调整,调整权值的目的在于突出重要单词,抑制次要单词。但是在本质上IDF是一种试图抑制噪音的加权 ,并且单纯地认为文本频数小的单词就越重要,文本频数大的单词就越无用,显然这并不是完全正确的。IDF的简单结构并不能有效地反映单词的重要程度和特征词的分布情况,使其无法很好地完成对权值调整的功能,所以TFIDF法的精度并不是很高。
此外,在TFIDF算法中并没有体现出单词的位置信息,对于Web文档而言,权重的计算方法应该体现出HTML的结构特征。特征词在不同的标记符中对文章内容的反映程度不同,其权重的计算方法也应不同。因此应该对于处于网页不同位置的特征词分别赋予不同的系数,然后乘以特征词的词频,以提高文本表示的效果。
模型概率
信息检索概述
信息检索是当前应用十分广泛的一种技术,论文检索、搜索引擎都属于信息检索的范畴。通常,人们把信息检索问题抽象为:在文档集合D上,对于由关键词w[1] … w[k]组成的查询串q,返回一个按查询q和文档d匹配度 relevance (q, d)排序的相关文档列表D’。
对于这一问题,先后出现了布尔模型、向量模型等各种经典的信息检索模型,它们从不同的角度提出了自己的一套解决方案。布尔模型以集合的布尔运算为基础,查询效率高,但模型过于简单,无法有效地对不同文档进行排序,查询效果不佳。向量模型把文档和查询串都视为词所构成的多维向量,而文档与查询的相关性即对应于向量间的夹角。不过,由于通常词的数量巨大,向量维度非常高,而大量的维度都是0,计算向量夹角的效果并不好。另外,庞大的计算量也使得向量模型几乎不具有在互联网搜索引擎这样海量数据集上实施的可行性。
tf-idf 模型
当前,真正在搜索引擎等实际应用中广泛使用的是 tf-idf 模型。tf-idf 模型的主要思想是:如果词w在一篇文档d中出现的频率高,并且在其他文档中很少出现,则认为词w具有很好的区分能力,适合用来把文章d和其他文章区分开来。
信息检索的概率视角
直观上看,tf 描述的是文档中词出现的频率;而 idf 是和词出现文档数相关的权重。我们比较容易定性地理解 tf-idf 的基本思想,但具体到 tf-idf 的一些细节却并不是那么容易说清楚为什么。
总结
TF-IDF 模型是搜索引擎等实际应用中被广泛使用的信息检索模型,但对于 TF-IDF 模型一直存在各种疑问。本文为信息检索问题一种基于条件概率的盒子小球模型,其核心思想是把“查询串q和文档d的匹配度问题”转化为“查询串q来自于文档d的条件概率问题”。它从概率的视角为信息检索问题定义了比 TF-IDF 模型所表达的匹配度更为清晰的目标。此模型可将 TF-IDF 模型纳入其中,一方面解释其合理性,另一方面也发现了其不完善之处。另外,此模型还可以解释 PageRank 的意义,以及 PageRank 权重和 TF-IDF 权重之间为什么是乘积关系。