文章目录
- 一. 位运算符脑图
- 二. 相关题目
- 1. 统计二进制数中0的个数
- 2. 数组中只出现一次的数字
- 3. 数组中只出现一次的数字 II
- 4. 不用加减乘除做加法
一. 位运算符脑图

二. 相关题目
1. 统计二进制数中0的个数
解题思路:x &= (x-1);它的作用是每次循环把 x 的二进制中从右往左数的最后一位1变成0,直道变成全0为止,循环结束。
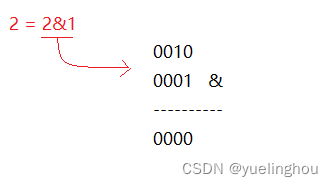
性能分析
- 时间复杂度:O(1),一般输入的数字都有固定的二进制位数。
- 空间复杂度:O(1),没有开辟额外的空间。
完整代码
size_t CountOne(int num)
{
size_t count = 0;
while(x)
{
++count;
// 通过这个迭代
// 每次可以消除x二进制位中的一个1
// 直到x最终为0
x = x&(x-1);
}
return count;
}
2. 数组中只出现一次的数字
题目连接
解题思路
- 首先利用异或运算的规律:0异或任何数得到任何数,相同的数异或得0,用0去异或数组中的每一个元素,得到两个只出现一次的数字(我们假设是AB)异或在一起的结果。
- 这个结果的二进制中的1,表现的是A和B在这个比特位上的数字是不同的。我们就取从左往右第一个1所在的位数,假设是第3位,接着把原数组分成两组,分组标准是第3位是否为1。如此**,出现两次的数依然会被分到同一个组**,因为相同数字所有位都相同;而不同的数,肯定不在一组。然后把这两个组按照最开始的思路,拿数字0去依次异或,剩余的两个结果就是这两个只出现一次的数字。
性能分析
- 时间复杂度:O(n)。n为数组的长度。
- 空间复杂度:O(1)。
完整代码
class Solution
{
public:
void FindNumsAppearOnce(vector<int> data,int* num1,int *num2)
{
// 数组元素为0或输出型参数为空直接结束
if(data.size() == 0 || num1 == nullptr || num2 == nullptr)
{
return;
}
// 1、算出两个只出现一次的数字异或在一起的结果
int ret = 0;
for(const auto e : data)
{
ret ^= e;
}
// 2、计算得到两个只出现一次的数字异或后最高比特位为1的位置
int bit = 0;
for(int i = 0; i < 32; ++i)
{
if((ret>>i) & 1)
{
bit = i;
}
}
// 3、分成两组分别求出两个只出现一次的数字
*num1 = 0;
*num2 = 0;
for(const auto e : data)
{
if(e & (1<<bit))
{
*num1 ^= e;
}
else
{
*num2 ^= e;
}
}
}
};
3. 数组中只出现一次的数字 II
题目连接
解题思路
首先如果我们不考虑这个只出现一次的数字,那么这个数组中的每一个数字都出现了三次。我们创建一个数组int count[32]去统计所有数的每一位比特位上一共有多少个1,统计结果 count 的每一个元素的值一定是 3n,如果把这个只出现一次的数字也给统计进去,那么 count 的每一个元素的值一定是3n 或 3n+1,根据 count 的每一个元素的值去模3,来还原出只那个出现一次的那个数字。
性能分析
- 时间复杂度:O(n)。n为数组的长度。
- 空间复杂度:O(1)。具体应该是数字的二进制位数,但一般输入的数字都有固定的二进制位数。
完整代码
class Solution {
public:
int singleNumber(vector<int>& nums)
{
// 1、统计所有数的每一位比特位上一共有多少个1
// 要么3n要么3n+1
vector<int> count(32);
for(auto& e : nums)
{
for(int i=0; i<32; ++i)// 遍历每一个元素的每一位比特位
{
if(e & (1<<i))
{
++count[i];
}
}
}
// 2、根据count的结果还原出只出现一次的那个数字
int ret=0;
for(int i=0; i<32; ++i)
{
if(count[i]%3)
{
ret |= (1<<i);
}
}
return ret;
}
};
4. 不用加减乘除做加法
题目连接
解题思路
-
二进制位异或运算相当于对应位相加,不考虑进位
比如:
1 ^ 1 = 0 —> 1 + 1 = 0 (当前位值为0,进一位)
1 ^ 0 = 1 —> 1 + 0 = 1 (当前位值为1)
0 ^ 0 = 0 —> 0 + 0 = 0 (当前位值为0) -
二进制位与运算相当于对应位相加之后的进位
比如:
1 & 1 = 1 —> 1 + 1 = 0 (当前位的值进一位)
1 & 0 = 0 —> 1 + 0 = 1 (当前位的值不进位)
0 & 0 = 0 —> 0 + 0 = 0 (当前位的值不进位) -
两个数相加:对应二进制位相加的结果 + 进位的结果
比如:
3 + 2 --> 0011 + 0010 --> 0011 ^ 0010 + ((0011 & 0010) << 1)
—> (0011 ^ 0010) ^ ((0011 & 0010) << 1), 当进位之后的结果为0时,相加结束
完整代码
class Solution {
public:
int add(int a, int b)
{
// 进位数为0时,结束循环
while(b)
{
// 得到二者和的无进位的结果
int notCarry=a^b;
// 得到进位数*10的结果
b=((unsigned int)(a&b))*2;
a=notCarry;
}
return a;
}
};