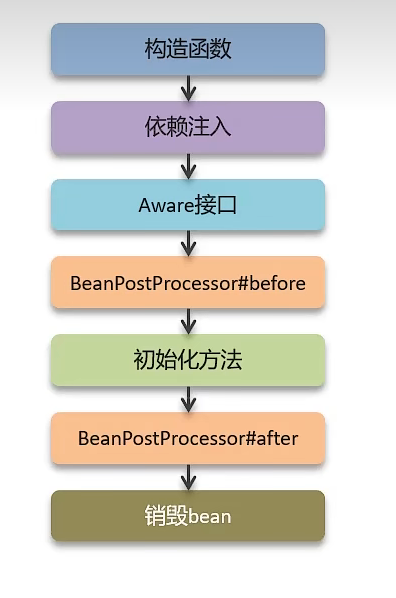
文献学习:
基于全过程通道相关像素值顺序的彩色图像可逆数据隐藏
原文题目:
Reversible data hiding for color images based on pixel value order of overall process channel.
发表期刊:
Signal Processing(中科院二区)
作者:
Ningxiong Mao, Hongjie He, Fan Chen, Lingfeng Qu等。
————————————————————————————————————————————
摘要
由于彩色图像在生活中的广泛应用,彩色图像可逆数据隐藏也备受关注。本文提出一种基于改进像素值排序的有效彩色图像RDH方案(框架)。在数据嵌入的全过程都充分利用信道间的相关性来提高嵌入性能。在预测阶段由于不同信道间相同位置块的像素值单调性一致,利用参考信道进行预排序使得大像素值被优先收集。然后在执行IPVO可以显著提高扩展预测误差数目。在块选择阶段,通过信道间的相关性提高块复杂度值的描述准确度,从而优先使用平滑块减少无效平移。在容量分配过程计算每个信道中的扩展预测误差与总的扩展预测误差比例,从而实现低计算复杂度及高精度的容量分配。
主要创新点
本文提出了一种全过程信道关联的彩色图像RDH算法。在预测值计算,像素块选择和容量分配都将使用信道间的关联性。由于PVO预测方法具有较高的精度,我们将PVO预测方法引入彩色图像RDH并通过信道间的关联性增强PVO的性能。本文的主要贡献如下。
- 新颖的预测方法基于信道间单调一致性的预测方法.将PVO预测方法引入到彩色图像中,
利用信道间的相关性对块内像素进行预排序增加了可扩展预测误差的数目。 - 利用信道间纹理相似的块选择方法.利用当前信道的上下文和参考信道相同位置块的纹理复杂度准确的描述当前像素块的复杂度,以减少无效平移。
- 兼顾信道间不同嵌入性能的容量分配方法.针对均等载荷分配的低精度和穷举方法的高计算复杂度。本文提出根据通道间的纹理特征进行载荷分配,提高了分配精度并且显著降低了时间复杂度。
算法
本文彩色图像RDH算法,主要包括预排序IPVO,像素块选择,容量分配和实现细节。整体框架如图1所示。
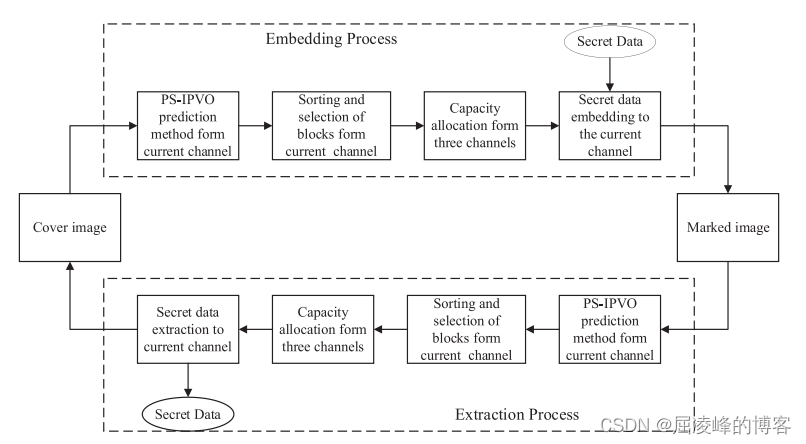
这里简要介绍下嵌入/提取过程:
将像素块分为空白块和阴影块,如图2 所示的棋盘模式。首先对阴影块进行数据嵌入,然后对空白块进行数据嵌入,并且空白块和阴影块各一半嵌入容量。由于空白块和阴影块的嵌入过程是类似的并且每个信道的嵌入过程也是类似的,所以本节以R信道空白块嵌入过程为例。本文的嵌入顺序是R-G-B,整个嵌入和提取过程如图2所示,提取是嵌入的逆过程。
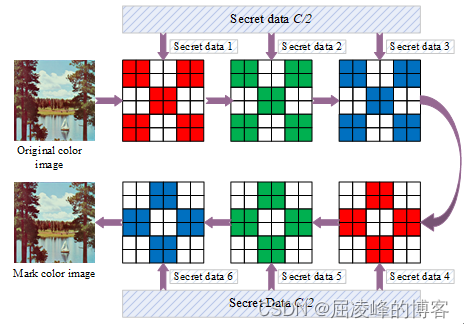
嵌入过程:
- 预处理. 为了防止像素值的上溢/下溢需要生成一个当前信道的标记位图,对于像素值为0 和 像素值 为 255 的像素进行标记,不进行数据嵌入,对得到的标记位图进行压缩得到一个短的比特流记为 LM。
- 嵌入准备. 首先我们通过光栅扫描顺序收集所有空白块。计算所有空白块的复杂度值根据公式(24),然后根据复杂度值进行升序排序确定空白块用来嵌入数据的顺序。根据SectionIII-C进行容量分配确定每个信道嵌入的容量比例。
- 数据嵌入. 通过PS-IPVO预测方法可以计算每一阴影块的预测误差。首先可以得到预测误差 e_max,根据公式(3) 进行第一轮数据嵌入和像素值修改。然后计算预测误差 e_min^R ,根据公式(6) 进行第二轮数据嵌入和像素值修改。
- 辅助信息嵌入. 在信道嵌入秘密数据完成后,会产生一些辅助信息包括分块大小(6 bits),嵌入结束位置(16 bits)和 标记位图LM (16 bits)。对这些辅助信息可以利用LSB 方法嵌入在信道的第一行。
上述是一个信道的数据嵌入过程,对其他信道也有类似的数据嵌入过程。在解码端,At decoder, 提取秘密数据和恢复像素值是嵌入的逆过程。
- 提取辅助信息. 首先是提取B信道空白块的辅助信息包括分块大小,嵌入结束位置 和标记压缩位图。
- 提取准备。通过光栅扫描收集所有的空白块计算每个块的复杂度值并进行升序排序确定空白块的提取顺序。根据SectionIII-D确定每个信道的容量比例。
- 秘密数据提取和图像恢复。通过PS-IPVO预测方法可以计算标记预测误差。根据标记预测误差和公式(7)可以无损的提取秘密数据,然后在进行第二轮的秘密数据提取和像素值恢复。对其他信道和空白块有类似的操作处理,如此可完成整个的数据提取和像素值恢复过程。
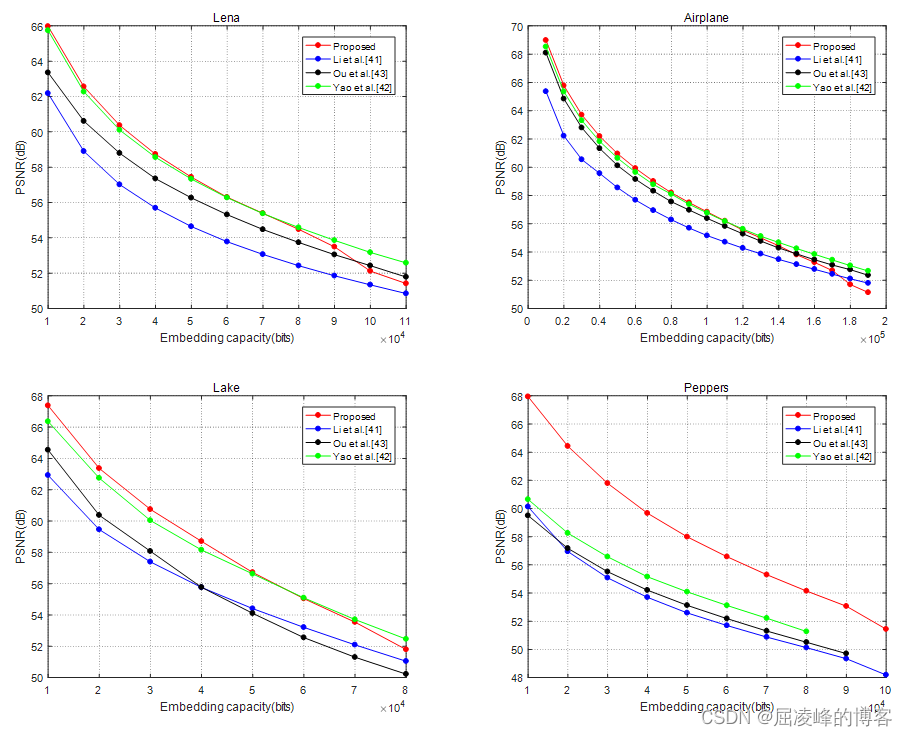
实验结果
结论
本文将PVO方法引入到彩色图像RDH。在数据嵌入过程都利用了信道之间的相关性包括预测方法,块选择和容量分配。PS-IPVO预测方法利用信道间的相关性进行预排序确保大像素值优先收集,从而增加了扩展预测误差数目。块选择过程利用信道间的相关性确保优先使用平滑块。通过不同信道间扩展预测误差的比例实现精确及低计算复杂度的容量分配。