目录
前言:
一:单值二叉树
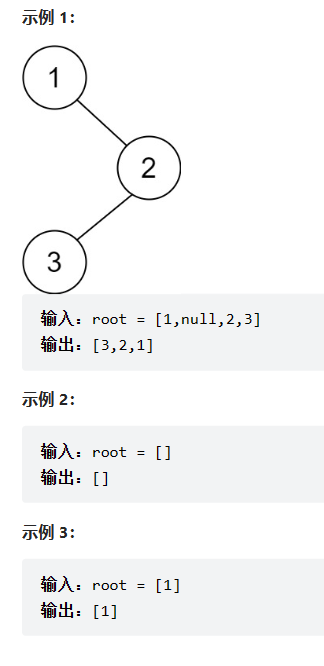
二:二叉树遍历
核心点
(1)前序
(2)中序
(3)后序
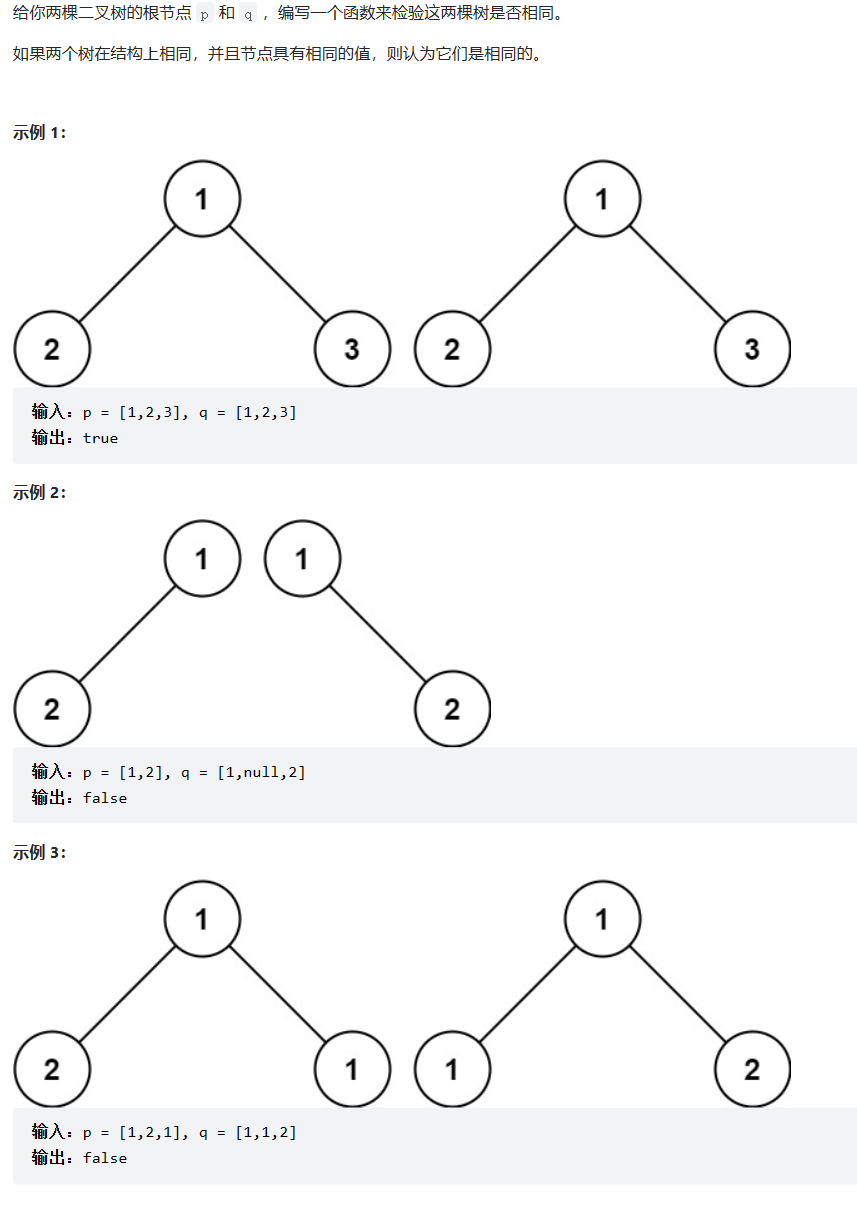
三:判断两颗树是否相同
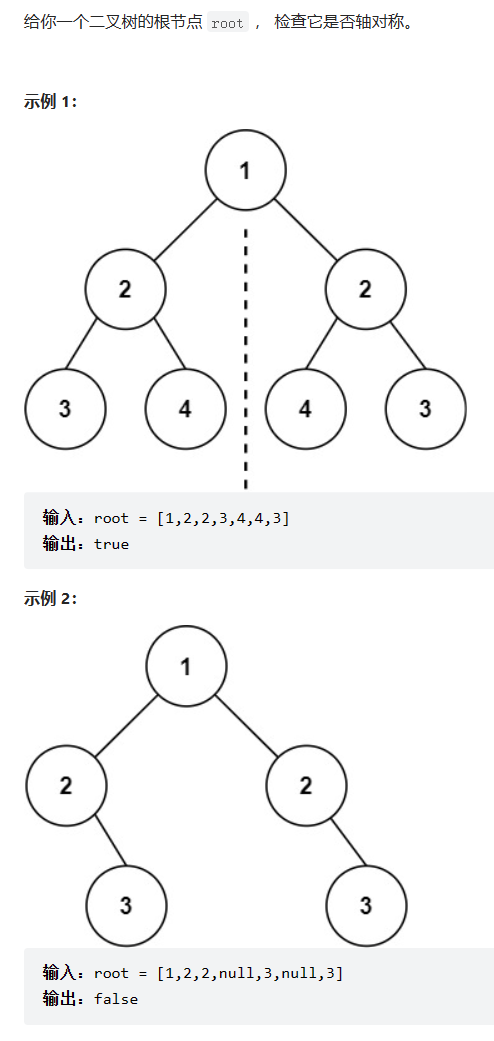
四:判断二叉树是否对称
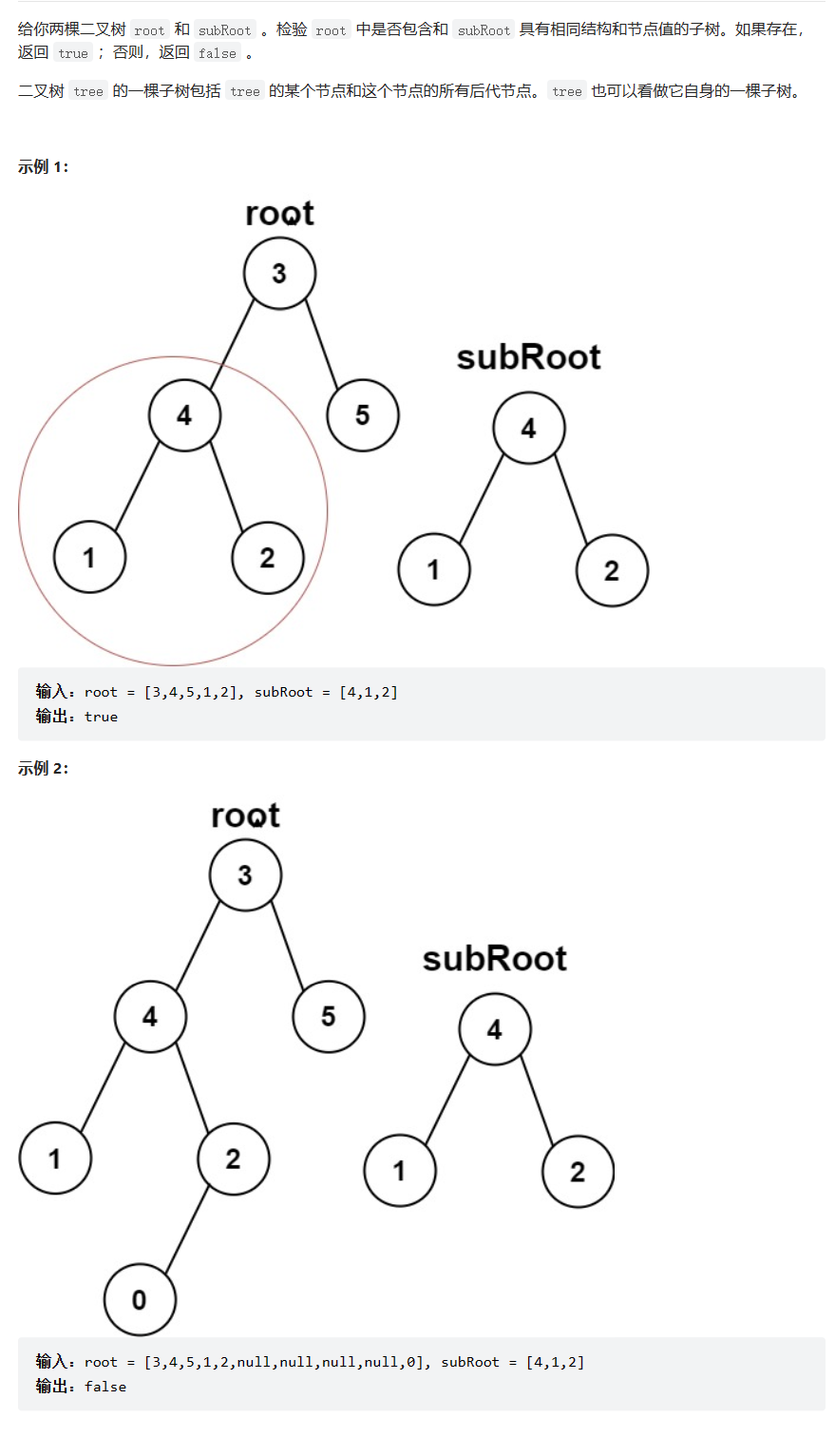
五:判断一颗树是否为另一颗树的子树
六:平衡二叉树
七:二叉树的构建加遍历
前言:
这一部分适合已经适用于已经掌握二叉树基础的同学(遍历,求节点数等)。
不清楚的同学可以先看之前一期:
https://blog.csdn.net/2301_76269963/article/details/130231257?spm=1001.2014.3001.5502
一:单值二叉树
题目链接:https://leetcode.cn/problems/univalued-binary-tree/submissions/
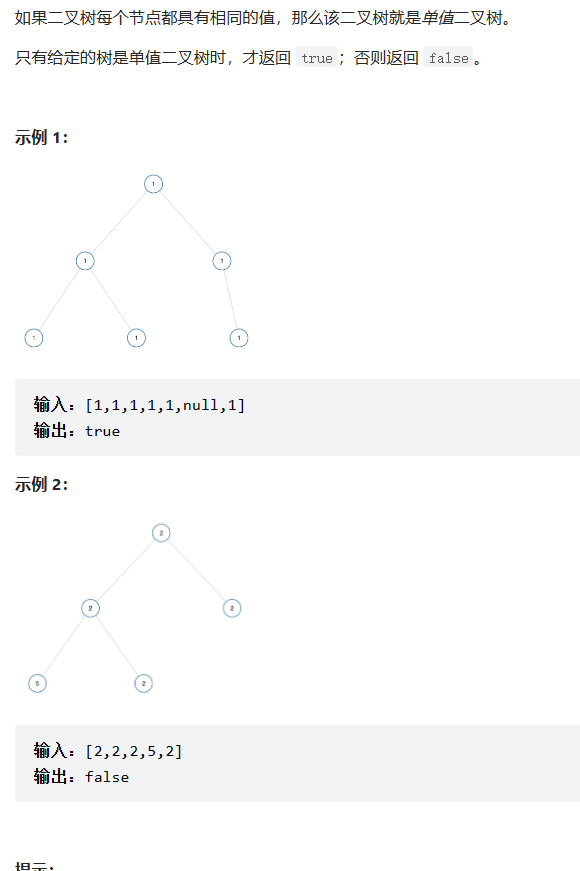
题目要求:
基础思路:
(1)首先判断根节点值与左右子树值是否相同,如果不同就返回 false。(注意如果左右子树为空不需要进行判断)
(2)否则,递归判断其左右子树是否为单值二叉树。(空树算作单值二叉树)
(3)如果一直到叶子节点都没有出现不相同的节点值,则返回 true,表示该树为单值二叉树。
(左子树右子树同时为单值树才行)
(这个题目比较简单,不利用递归也可以实现,但是需要建立辅助栈,只要遍历所有节点依次判断,遇到不同返回false,遍历完都没有不同返回true)
代码:
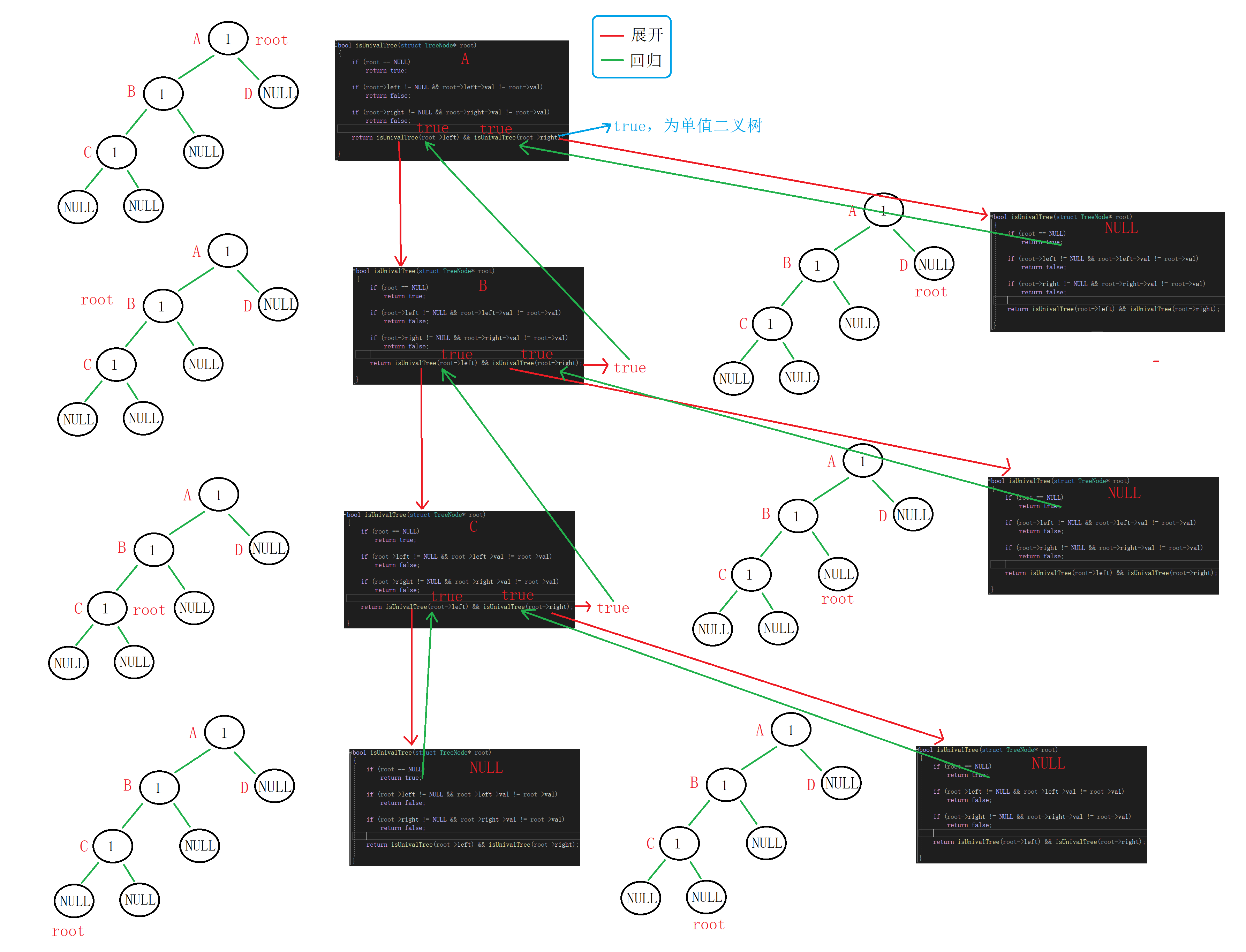
bool isUnivalTree(struct TreeNode* root) { if(root == NULL) { return true; } if(root->left!=NULL && root->left->val != root->val) { return false; } if(root->right!=NULL && root->right->val != root->val) { return false; } return isUnivalTree(root->left) && isUnivalTree(root->right); }图解:
二:二叉树遍历
核心点
(1)我们知道在函数调用时候形参只是实参的临时拷贝,如果我们直接传值调用,是没办法直接与那个变量建立联系的。
(2)如果我们想让函数不管递归深度多大都始终使用一个变量,我们应该进行传址调用。
(1)前序
题目链接:https://leetcode.cn/problems/binary-tree-preorder-traversal/submissions/
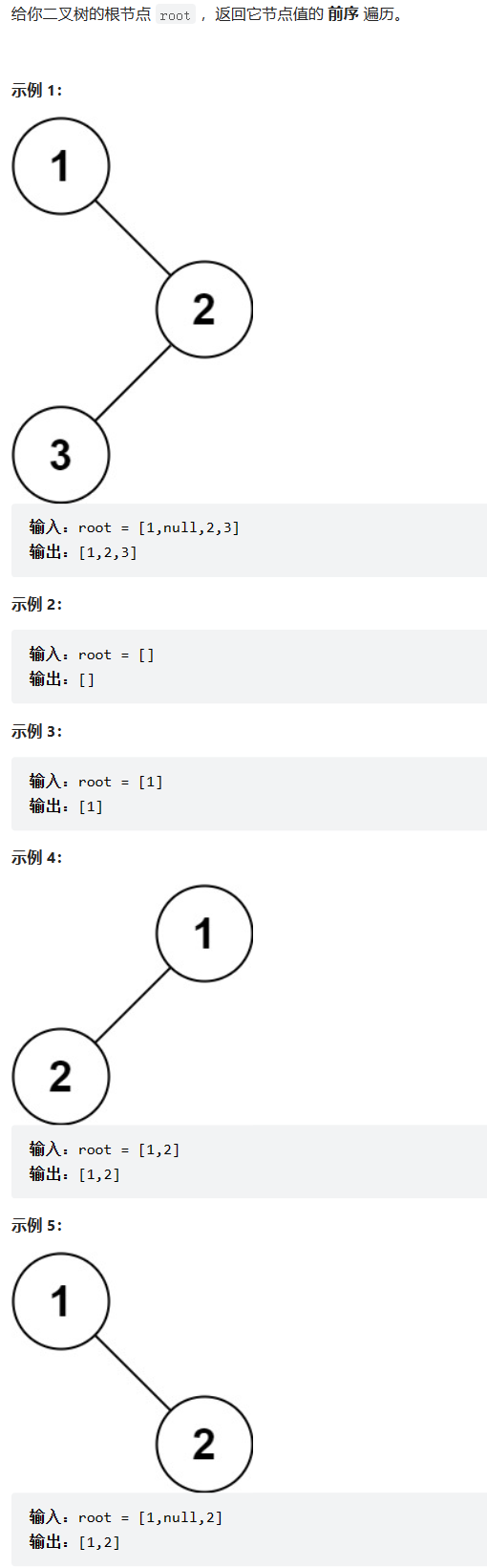
题目要求:
思路:
①和我们之前的打印不同,这一次遍历是要把节点数据存入数组中
②先求节点数(之前一次讲过),依据节点数来开辟空间
③先存储数据,再递归走左子树,后递归走右子树,每一次存储完成都要让(*i)加1(本体加1)
④记得为(*returnSize)赋值数组元素个数,告知元素个数,别人才能进行测试
代码:
//求树的节点数 int BinaryTreeSize(struct TreeNode* root) { return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1; } void _preorderTraversal(struct TreeNode* root,int* a,int* i) { if(root == NULL) { return; } //赋值 a[*i] = root->val; *i+=1; //左子树 _preorderTraversal(root->left,a,i); //右子树 _preorderTraversal(root->right,a,i); } int* preorderTraversal(struct TreeNode* root, int* returnSize) { //申请空间存储数据 int size=BinaryTreeSize(root); int* a=(int*)malloc(sizeof(int)*size); //遍历存储数据(利用子函数) int i=0; _preorderTraversal(root,a,&i); //返回 *returnSize = size; return a; }
(2)中序
题目链接:https://leetcode.cn/problems/binary-tree-inorder-traversal/submissions/
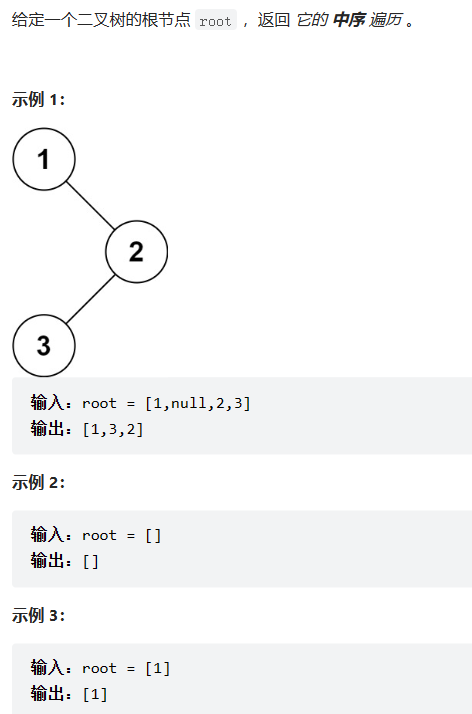
题目要求:
思路:与前序基本一致,只是换了存储的顺序
代码:
//求树的节点数 int BinaryTreeSize(struct TreeNode* root) { return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1; } void _inorderTraversal(struct TreeNode* root,int* a,int* i) { if(root == NULL) { return; } _inorderTraversal(root->left,a,i); a[*i] = root->val; *i += 1; _inorderTraversal(root->right,a,i); } int* inorderTraversal(struct TreeNode* root, int* returnSize) { //申请空间存储数据 int size = BinaryTreeSize(root); int* a = (int*)malloc(sizeof(int)*size); //调用子函数存储 int i=0; _inorderTraversal(root,a,&i); //返回 *returnSize = size; return a; }
(3)后序
题目链接:https://leetcode.cn/problems/binary-tree-postorder-traversal/submissions/
题目要求:
思路:与前序基本一致,只是换了存储的顺序
代码:
//求树的节点数 int BinaryTreeSize(struct TreeNode* root) { return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1; } void _postorderTraversal(struct TreeNode* root,int* a,int* i) { if(root == NULL) { return; } //左子树 _postorderTraversal(root->left,a,i); //右子树 _postorderTraversal(root->right,a,i); //存储 a[*i] = root->val; *i += 1; } int* postorderTraversal(struct TreeNode* root, int* returnSize) { //申请空间存储 int size = BinaryTreeSize(root); int* a = (int*)malloc(sizeof(int)*size); //调用子函数遍历存储 int i=0; _postorderTraversal(root,a,&i); //返回 *returnSize = size; return a; }
三:判断两颗树是否相同
题目链接:https://leetcode.cn/problems/same-tree/submissions/
题目要求:
基础思路:
(1)先判断节点地址,如果两边都为空返回true,一边为空一边不为空返回false
(2)然后判断根部数据是否相同,不同返回false
(3)否则递归判断左子树和右子树是否相同
(4)除了根部以外,左右子树都相同两棵树才相同
代码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) { if(p == NULL && p==q) { return true; } if(p==NULL || q==NULL) { return false; } if(p->val != q->val) { return false; } return isSameTree(p->left,q->left) && isSameTree(p->right,q->right); }
四:判断二叉树是否对称
题目链接:https://leetcode.cn/problems/symmetric-tree/submissions/
题目要求:
基础思路:
(1)和前面判断两棵树是否相同很相似,这里相当于把左右子树当成1树和2树
(2)先判断节点地址,如果两边都为空返回true,一边为空一边不为空返回false
(3)先比较根部是否相同,不同返回false
(4)根部相同,递归判断1树左子树与2树右子树是否相同,1树右子树与2树左子树是否相同
(5)到叶子节点依然相同,说明这颗树轴对称
代码:
bool CheckSymmetry(struct TreeNode* left,struct TreeNode* right) { //如果都为空,对称 if(left == NULL && left == right) { return true; } //一方为空一方不为,不对称 if(left == NULL || right == NULL) { return false; } if(left->val != right->val) { return false; } return CheckSymmetry(left->left,right->right) && CheckSymmetry(left->right,right->left); } bool isSymmetric(struct TreeNode* root) { //利用子函数判断是否对称 return CheckSymmetry(root->left,root->right); }
五:判断一颗树是否为另一颗树的子树
题目链接:https://leetcode.cn/problems/subtree-of-another-tree/
题目要求:
基础思路:
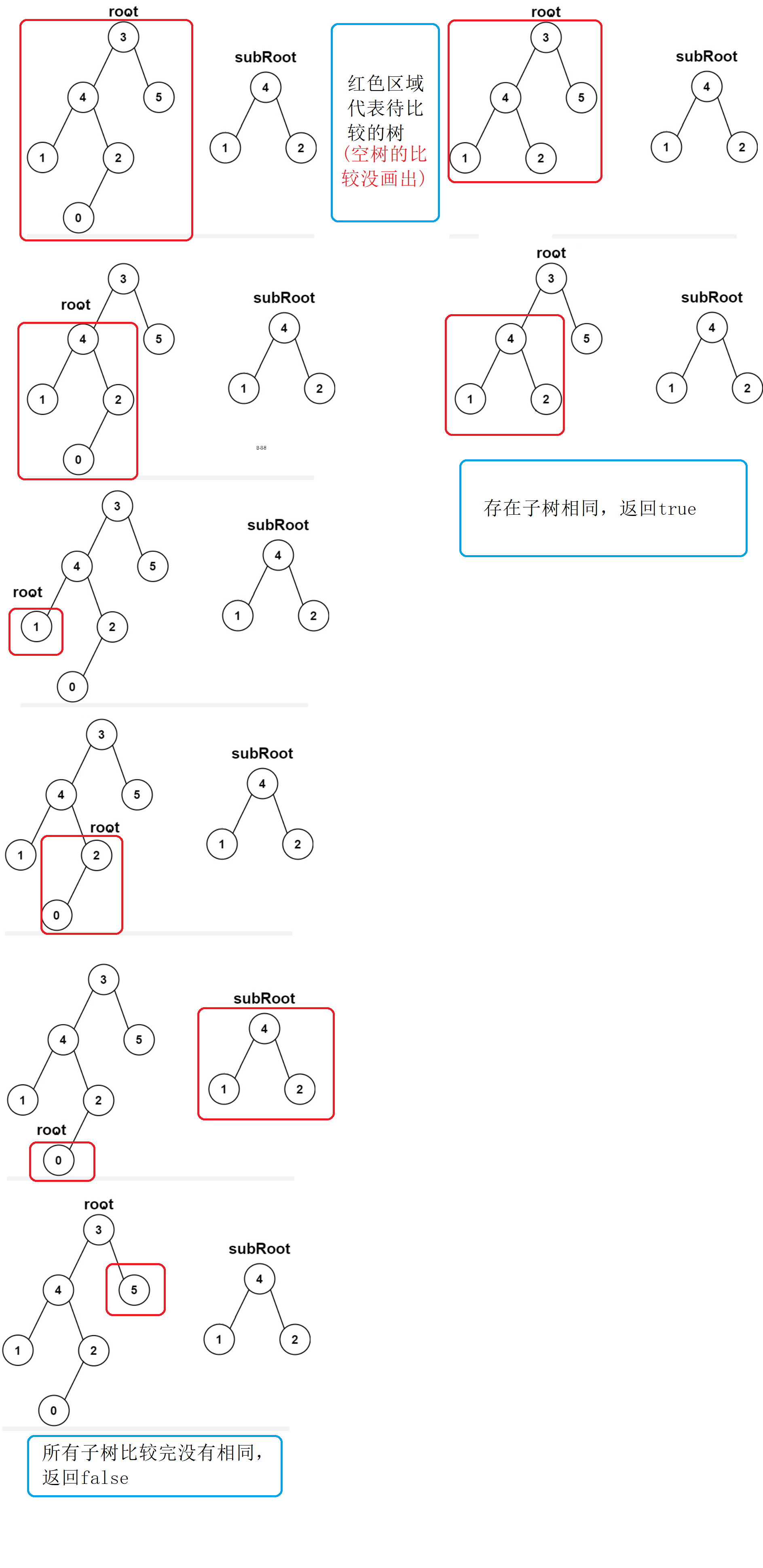
(1)大致思路就是拿母树的每一个子树依次和subRoot比较
有相同的返回true,否则返回false
(2)如果母树为空,返回false
(3)利用前面判断两棵树是否相同的函数,我们先判断母树与subRoot是否相同
(4)相同返回true,不同就递归走母树的左子树和右子树
(5)左右子树只要有一方相同就为true
代码:
//判断两颗树是否相同 bool isSameTree(struct TreeNode* p, struct TreeNode* q) { if(p == NULL && p==q) { return true; } if(p==NULL || q==NULL) { return false; } if(p->val != q->val) { return false; } return isSameTree(p->left,q->left) && isSameTree(p->right,q->right); } bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) { if(root == NULL) { return false; } if(isSameTree(root,subRoot)) { return true; } return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot); }图解:
六:平衡二叉树
题目链接:https://leetcode.cn/problems/balanced-binary-tree/
题目要求:
基础思路:
(1)节点为空返回true(空树也是平衡二叉树)
(2)利用函数(之前讲过)计算当前节点的左右子树的高度差
(3)如果高度差不超过 1,则递归判断其左右子树是否为平衡二叉树
(4)如果有任何一个节点的左右子树的高度差大于 1,则该树不是平衡二叉树
代码:
//求树高度 int BinaryTreeDepth(struct TreeNode* root) { if (root == NULL) { return 0; } if (root->left == NULL && root->right == NULL) { return 1; } return fmax(BinaryTreeDepth(root->left), BinaryTreeDepth(root->right)) + 1; } bool isBalanced(struct TreeNode* root) { if(root == NULL) return true; int leftDepth = BinaryTreeDepth(root->left); int rightDepth = BinaryTreeDepth(root->right); return abs(leftDepth-rightDepth)>1?false: isBalanced(root->left)&&isBalanced(root->right); }
七:二叉树的构建加遍历
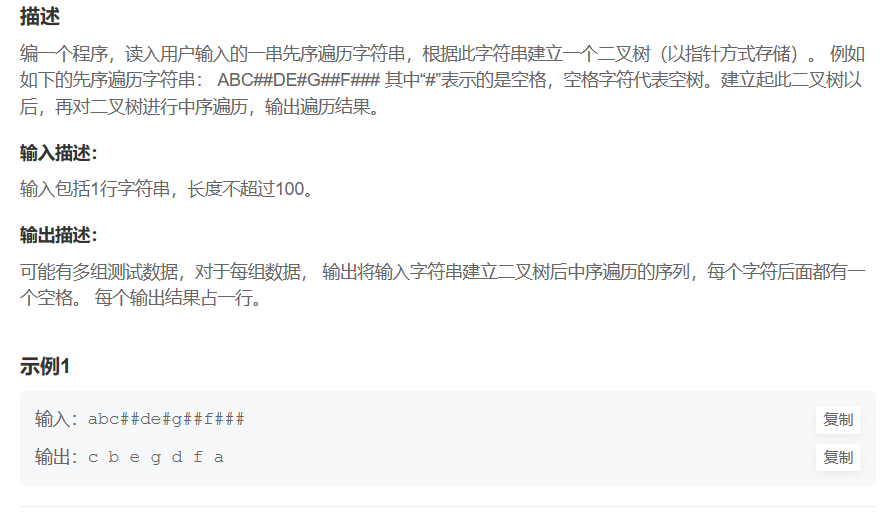
题目链接:https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef?tpId=0&difficulty=&judgeStatus=&tags=&title=%E4%BA%8C%E5%8F%89%E6%A0%91&sourceUrl=&gioEnter=menu
题目要求:
基础思路:
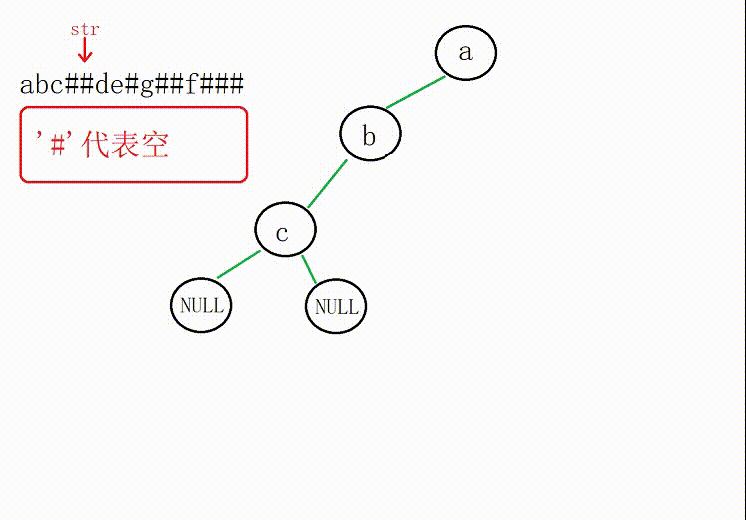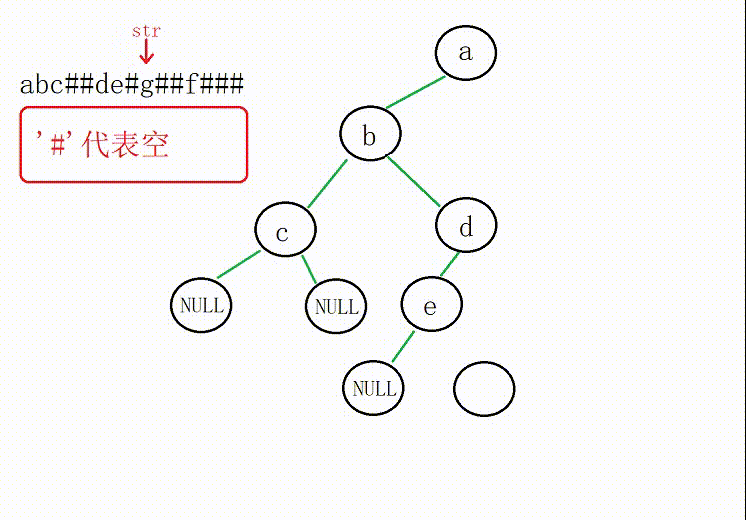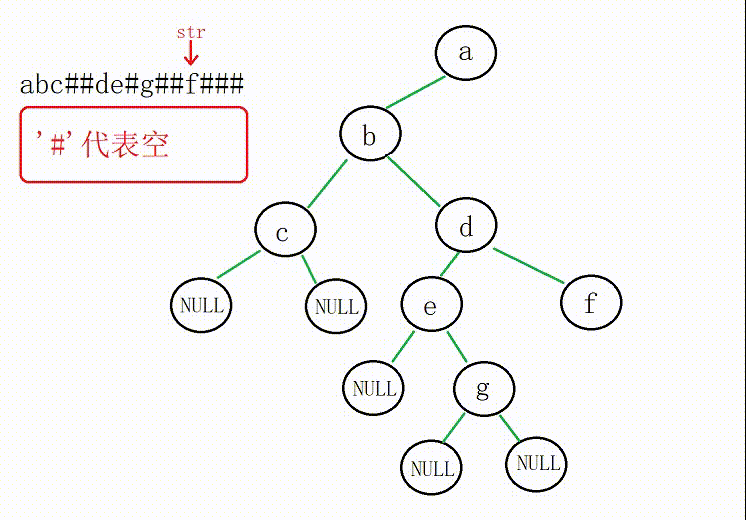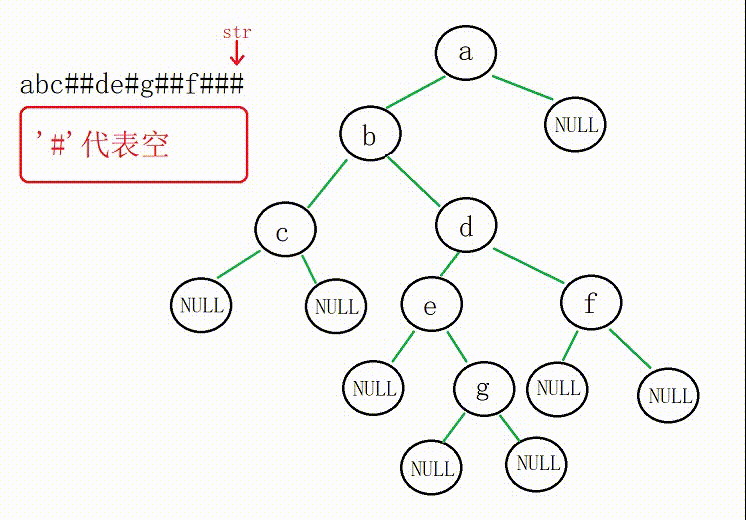
(1)依据输入的字符串建树(递归)
①创建的顺序是先左子树后右子树
②为了确保递归过程中使用同一个变量,我们传下标的地址
如果字符为'#'或者'\0'(字符串走到空),节点地址赋值为空
③返回创建好的树的根部节点地址
图解:
(2)进行中序遍历(之前讲过,不赘述)
代码:
#include <stdio.h> #include <stdlib.h> typedef char BTDataType; typedef struct BinaryTreeNode { //存储左孩子的地址 struct BinaryTreeNode* left; //存储右孩子的地址 struct BinaryTreeNode* right; BTDataType data; }BTNode; BTNode* maketree(char*arr,int* i) { if(arr[*i]=='#'||arr[*i]=='\0') { return NULL; } BTNode* newnode = (BTNode*)malloc(sizeof(BTNode)); newnode->data = arr[(*i)++]; newnode->left = maketree(arr,i); //这里加1是因为字符为'#'时候直接返回了空 //我们要走到下一个字符就要进行自加 (*i)++; newnode->right = maketree(arr,i); return newnode; } //中序遍历 void InOrder(BTNode* root) { if(root == NULL) { return; } //左树 InOrder(root->left); //打印 printf("%c ", root->data); //右树 InOrder(root->right); } int main() { //字符串长度不超过100 char str[100]= {0}; //可能有多组输入 while(scanf("%s",str) != EOF) { //建树 int i = 0; BTNode* root = maketree(str,&i); //遍历 InOrder(root); } return 0; }