文章目录
- stack的介绍
- stack的使用
stack的介绍
stack是一种容器适配器,专门用在具有后进先出操作特性的环境中,只能在容器的一端进行插入删除;stack是作为容器适配器被实现的,容器适配器即是对特性类封装作为其底层的容器,并提供一组特定的成员函数来访问其元素。
stack的底层容器可以是任何标准的容器类模板或者一些其他特定的容器类,这些容器类应该支持以下操作:empty(判空操作)、back(获取尾部元素操作)、push_back(尾部插入元素操作)、pop_back(尾部删除元素操作)。
标准容器vector、deque、list均符合这些需求,默认情况下,如果没有为stack指定特定的底层容器,则使用deque。
stack的使用
| 函数声明 | 接口说明 |
|---|---|
| stack() | 构造空的栈 |
| empty() | 检测stack是否为空,为空返回真,否则返回假 |
| size() | 返回stack中元素的个数 |
| top() | 返回栈顶元素的引用 |
| push() | 将元素压入stack中 |
| pop() | 将stack中尾部的元素弹出 |
int main()
{
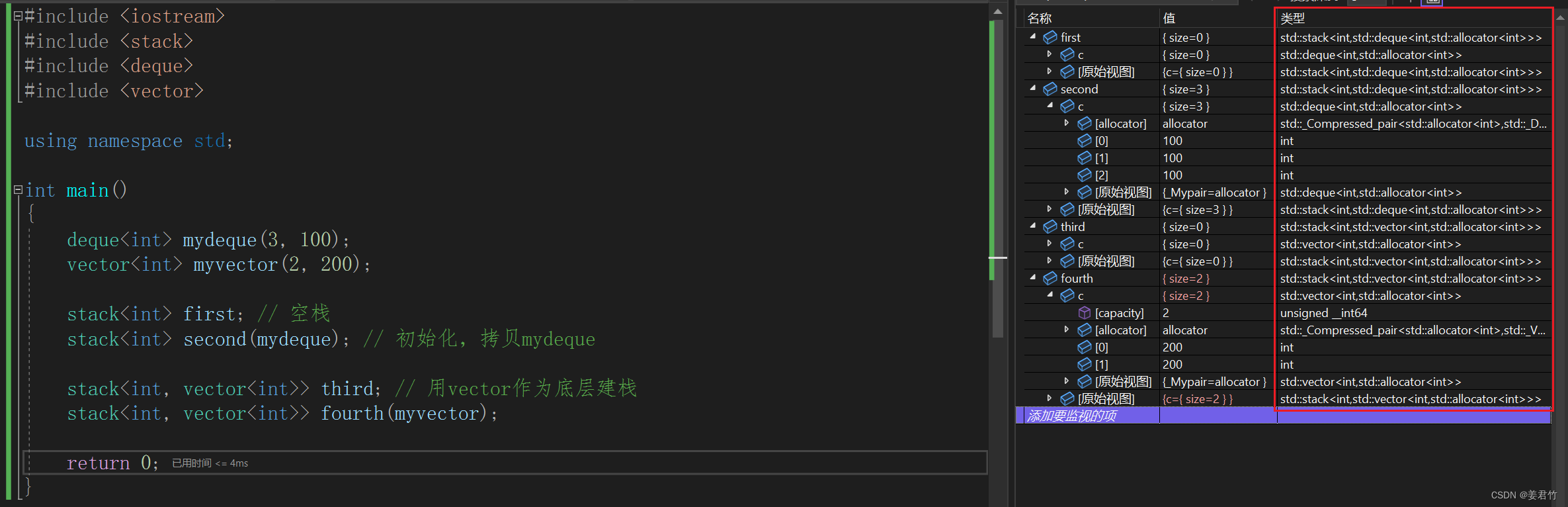
deque<int> mydeque(3, 100);
vector<int> myvector(2, 200);
stack<int> first; // 空栈
stack<int> second(mydeque); // 初始化,拷贝mydeque
stack<int, vector<int>> third; // 用vector作为底层建栈
stack<int, vector<int>> fourth(myvector);
return 0;
}
这里注意看数据类型,直接构造的栈,默认使用的是deque,而我们用stack<int, vector<int>>构造的栈则是使用了vector。
empty是检测stack的size是否为0来判断是否为空的。
push成员函数调用的是底层容器的push_back函数,实现尾插的功能。标准容器vector、deque、list都是拥有push_back这一成员函数的。
pop成员函数则是调用的底层容器的pop_back函数,实现尾删的功能。同样的,这几个标准容器也是拥有pop_back这一成员函数的。
因为stack的特性是先进后出,也就是说插入删除只会在尾部进行,所以没有push_front和pop_front,所以直接用push和pop来表示。
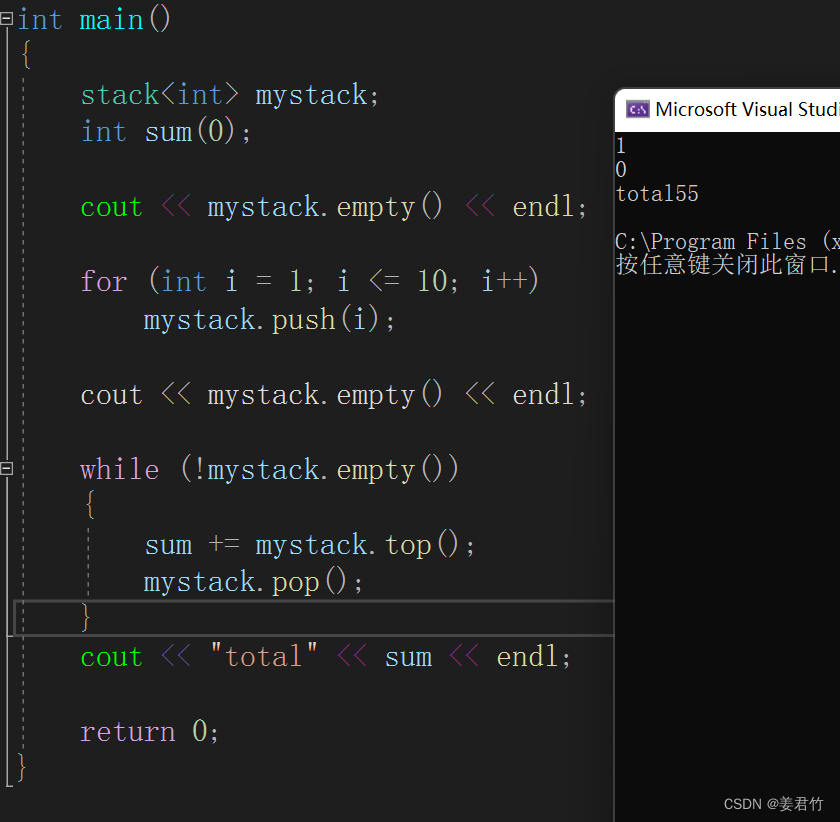
int main()
{
stack<int> mystack;
int sum(0);
cout << mystack.empty() << endl;
for (int i = 1; i <= 10; i++)
mystack.push(i);
cout << mystack.empty() << endl;
while (!mystack.empty())
{
sum += mystack.top();
mystack.pop();
}
cout << "total" << sum << endl;
return 0;
}
size函数实现则是因为stack本身就具有一个size_type属性。
int main()
{
stack<int> myints;
cout << "1.size:" << myints.size() << endl;
for (int i = 0; i < 5; i++)
myints.push(i);
cout << "2.size:" << myints.size() << endl;
myints.pop();
cout << "3.size:" << myints.size() << endl;
return 0;
}

top成员函数是通过底层容器中的back函数实现的,back函数返回的是容器中的最后一个元素,正好符合top函数的功能。因为返回的是引用,所以可以被修改。
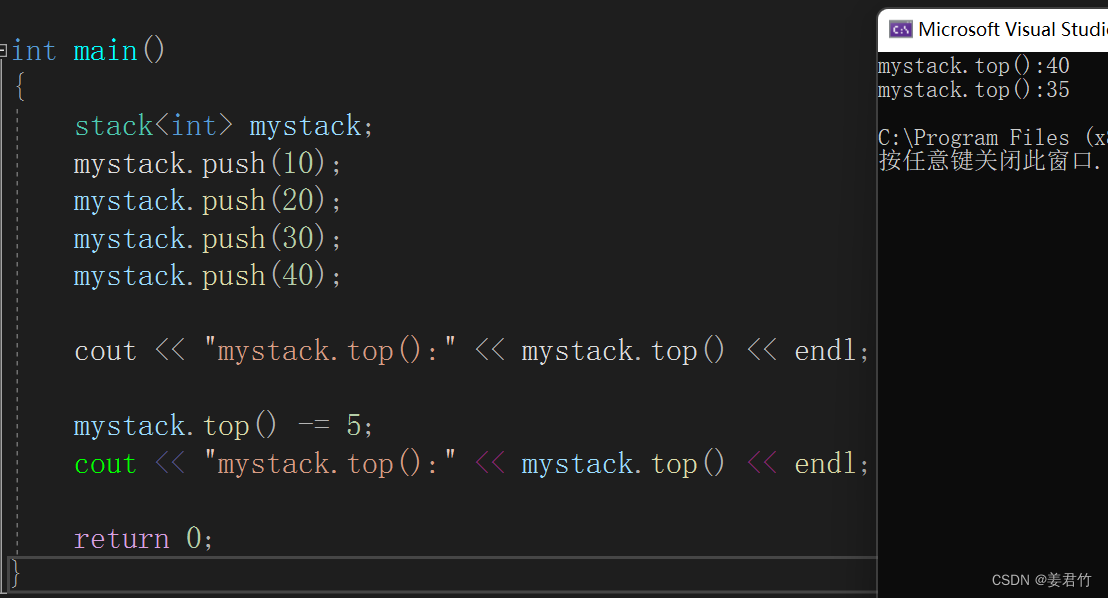
int main()
{
stack<int> mystack;
mystack.push(10);
mystack.push(20);
mystack.push(30);
mystack.push(40);
cout << "mystack.top():" << mystack.top() << endl;
mystack.top() -= 5;
cout << "mystack.top():" << mystack.top() << endl;
return 0;
}
在C++11中,stack的成员函数新增了emplace和swap,emplace的作用是插入一个新元素,并重新构造;swap则是交换内容。不过有一个非成员函数swap也可以实现这一功能。