本人研一,简单记录下上课的大作业,如果你不会自己写,相信你有缘能找到这篇博客
线性回归模型
1.实验内容
图像是一种非常常见的信息载体,但是在图像的获取、传输、存储过程中可能由于各种原因使得图像受到噪声的影响。如何去除噪声的影响,恢复图像原本的信息是计算机视觉中的重要研究问题。
常见的图像恢复算法有基于空间域的中值滤波、基于小波域的小波去噪、基于偏微分的非线性扩散滤波等。本次实验要对图像添加高斯噪声,并对添加噪声的图像进行基于线性回归模型的去噪
2.实验要求
(1) 生成受损图像

3.实验环境
可以基于Python的OpencCV库进行图像相关处理,使用Numpy库进行相关数值运算。
4.程序代码
废话不多说直接上代码
from matplotlib import pyplot as plt
import numpy as np
import cv2 # opencv库
from sklearn.linear_model import LinearRegression, Ridge, Lasso # 回归分析
def read_image(img_path):
"""
读取图片,图片是以 np.array 类型存储,返回图片的数组形式
:param img_path: 图片的路径以及名称
:return: img np.array 类型存储
"""
# 读取图片
img = cv2.imread(img_path)
# 如果图片是三通道,采用 matplotlib 展示图像时需要先转换通道
if len(img.shape) == 3:
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # 转换围为二通道的灰度图
return img
def plot_image(image, image_title, is_axis=False):
"""
展示图像
:param image: 展示的图像,一般是 np.array 类型
:param image_title: 展示图像的名称
:param is_axis: 是否需要关闭坐标轴,默认展示坐标轴
:return:
"""
# 展示图片
plt.imshow(image)
# 关闭坐标轴,默认关闭
if not is_axis:
plt.axis('off')
# 展示受损图片的名称
plt.title(image_title)
# 展示图片
plt.show()
def save_image(filename, image):
"""
保存图片,将np.ndarray 图像矩阵保存为一张 png 或 jpg 等格式的图片
:param filename: 图片保存路径及图片名称和格式
:param image: 图像矩阵,一般为np.array
:return:无返回值
"""
# np.copy() 函数创建一个副本,复制到img变量中
img = np.copy(image)
# 从给定数组的形状中删除一维的条目f
img = img.squeeze()
# 将图片数据存储类型改为 np.uint8
if img.dtype == np.double:
# 若img数据存储类型是 np.double ,则转化为 np.uint8 形式
img = img * np.iinfo(np.uint8).max
# 转换图片数组数据类型
img = img.astype(np.uint8) # .astype()将数据类型转换为括号的的类型
img = cv2.cvtColor(img, cv2.COLOR_RGB2BGR)
# 生成图片
cv2.imwrite(filename, img) # cv2.imwrite() 用于将图像保存到指定的文件
def normalization(image):
"""
将数据线性归一化
:param image: 图片矩阵,一般是np.array 类型
:return: 将归一化后的数据,在(0,1)之间
"""
# 获取图片数据类型对象的最大值和最小值,比如int16范围[-32768,32768]
info = np.iinfo(image.dtype)
# 图像数组数据放缩在 0-1 之间,并转换为双精度
return image.astype(np.double) / info.max
def noise_mask_image(img, noise_ratio):
"""
生成受损图片
:param img: 图像矩阵,一般为 np.ndarray
:param noise_ratio: 噪声比率,可能值是0.4/0.6/0.8
:return: noise_img 受损图片, 图像矩阵值 0-1 之间,数据类型为 np.array,
数据类型对象 (dtype): np.double, 图像形状:(h,w,c),顺序为RGB
"""
# 受损图片初始化
noise_img = None
# -------------生成受损图像-----------------
row, col = img.shape[0], img.shape[1] # 图片高宽
rgb = [None, None, None] # rgb初始化
for i in range(3):
# 构造其中一个通道的噪声图
for j in range(row): # 第几行
if rgb[i] is None:
rgb[i] = np.random.choice(2, (1, col), p=[noise_ratio, 1 - noise_ratio])
else:
a = np.random.choice(2, (1, col), p=[noise_ratio, 1 - noise_ratio]) # 从0,1两个数根据概率,重复选择col次,列数,0为施加噪声
rgb[i] = np.concatenate((rgb[i], a), axis=0) # 将产生的噪声加到初始化的rgb上
# 扩展 shape
for i in range(3):
rgb[i] = rgb[i][:, :, np.newaxis] # 变成三维
# 合并
rst = np.concatenate((rgb[0], rgb[1], rgb[2]), axis=2) # 同个维度拼接
noise_img = rst * img # 噪声与原图逐元素相乘
# -----------------------------------------------
return noise_img
def get_noise_mask(noise_img):
"""
获取噪声图像的矩阵形式,一般为 np.array
:param noise_img: 带有噪声的图片
:return: 噪声图像矩阵
"""
# 将图片数据矩阵只包含 0和1,如果不能等于 0 则就是 1。
return np.array(noise_img != 0, dtype='double')
def compute_error(res_img, img):
"""
计算恢复图像 res_img 与原始图像 img 的 2-范数,向量元素绝对值的平方和再开方
:param res_img:恢复图像
:param img:原始图像
:return: 恢复图像 res_img 与原始图像 img 的2-范数
"""
# 初始化
error = 0.0
# 将图像矩阵转换成为np.narray
res_img = np.array(res_img)
img = np.array(img)
# 如果2个图像的形状不一致,则打印出错误结果,返回值为 None
if res_img.shape != img.shape:
print("shape error res_img.shape and img.shape %s != %s" % (res_img.shape, img.shape))
return None
# 计算图像矩阵之间的评估误差
error = np.sqrt(np.sum(np.power(res_img - img, 2)))
return round(error, 3)
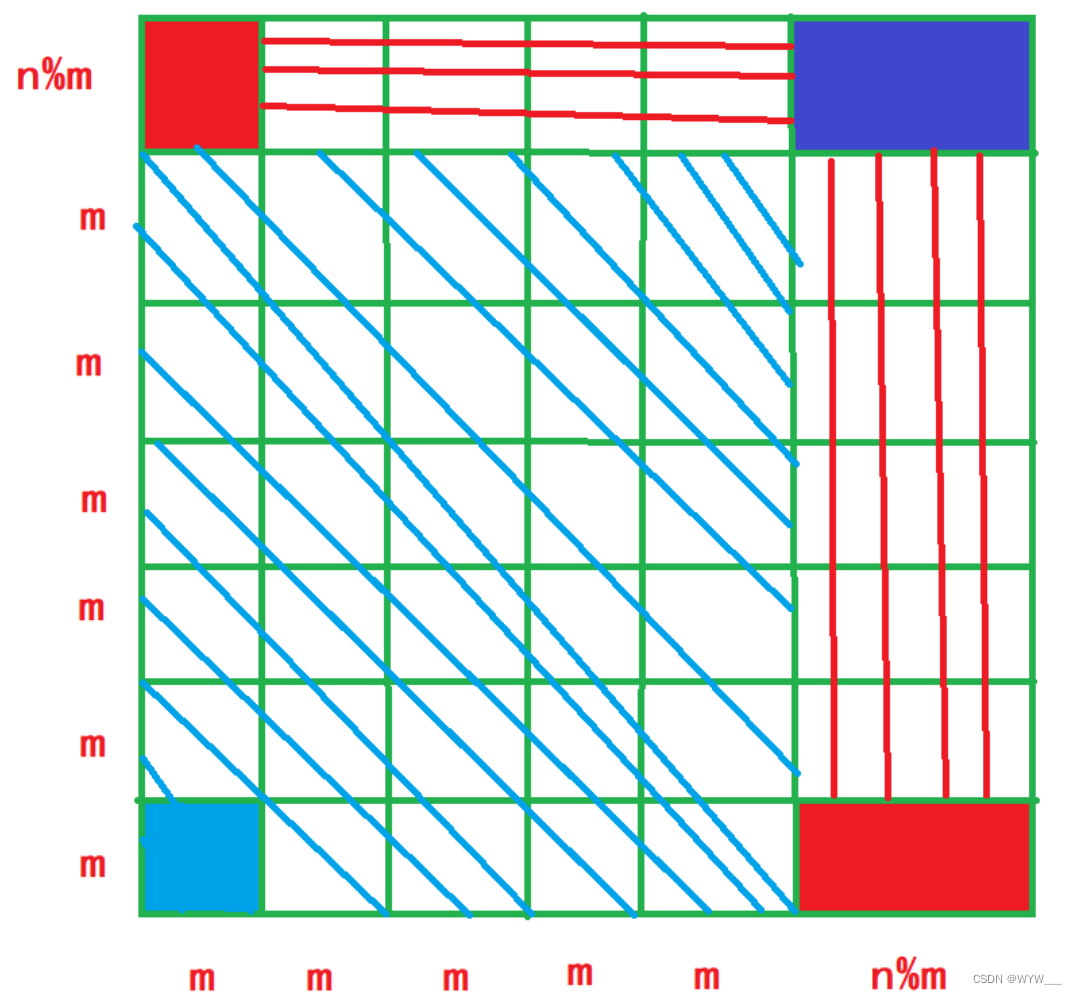
def restore_image(noise_img, size=4):
"""
使用区域二元线性回归模型 进行图像恢复。
:param noise_img: 一个受损的图像
:param size: 输入区域半径,长宽是以 size*size 方形区域获取区域, 默认是 4
:return: res_img 恢复后的图片,图像矩阵值 0-1 之间,数据类型为 np.array,
数据类型对象 (dtype): np.double, 图像形状:(height,width,channel), 通道(channel) 顺序为RGB
"""
# 恢复图片初始化,首先 copy 受损图片,然后预测噪声点的坐标后作为返回值。
res_img = np.copy(noise_img)
# 获取噪声图像
noise_mask = get_noise_mask(noise_img)
# -------------恢复图像----------------------------
rows, cols, channel = res_img.shape
region = 10 # 10 * 10的区域
row_cnt = rows // region
col_cnt = cols // region
for chan in range(channel):
for rn in range(row_cnt + 1):
ibase = rn * region
if rn == row_cnt:
ibase = rows - region
for cn in range(col_cnt + 1):
jbase = cn * region
if cn == col_cnt:
jbase = cols - region
x_train = []
y_train = []
x_test = []
for i in range(ibase, ibase + region):
for j in range(jbase, jbase + region):
if noise_mask[i, j, chan] == 0: # 噪音点
x_test.append([i, j])
continue
x_train.append([i, j])
y_train.append([res_img[i, j, chan]])
if x_train == []:
print("x_train is None")
continue
reg = LinearRegression()
reg.fit(x_train, y_train)
pred = reg.predict(x_test)
for i in range(len(x_test)):
res_img[x_test[i][0], x_test[i][1], chan] = pred[i][0]
res_img[res_img > 1.0] = 1.0
res_img[res_img < 0.0] = 0.0
# ---------------------------------------------------------------
return res_img
if __name__ == "__main__":
img_path = '12.jpg' # 图片路径
img = read_image(img_path)
noise_ratio = 0.4 # 噪声比
nor_img = normalization(img)
print(nor_img.shape)
# 生成受损图片
for i in range(3):
noise_img = noise_mask_image(nor_img, noise_ratio)
# 保存受损图片
save_image('result/damaged_' + str(noise_ratio) + '.png', noise_img)
# 恢复图片
res_img = restore_image(noise_img)
# 保存恢复图片
save_image('result/recovery_' + str(noise_ratio) + '.png', res_img)
print("{}噪声比率,噪声图和原图之间的误差: {}".format(noise_ratio,compute_error(noise_img, nor_img)))
print("{}噪声比率,恢复图和原图之前的误差: {}".format(noise_ratio,compute_error(res_img, nor_img)))
noise_ratio = round(noise_ratio+0.2,3)
# 展示恢复图片
# plot_image(image=res_img, image_title="restore image")
直接拉到最后,看main函数,需要改的地方
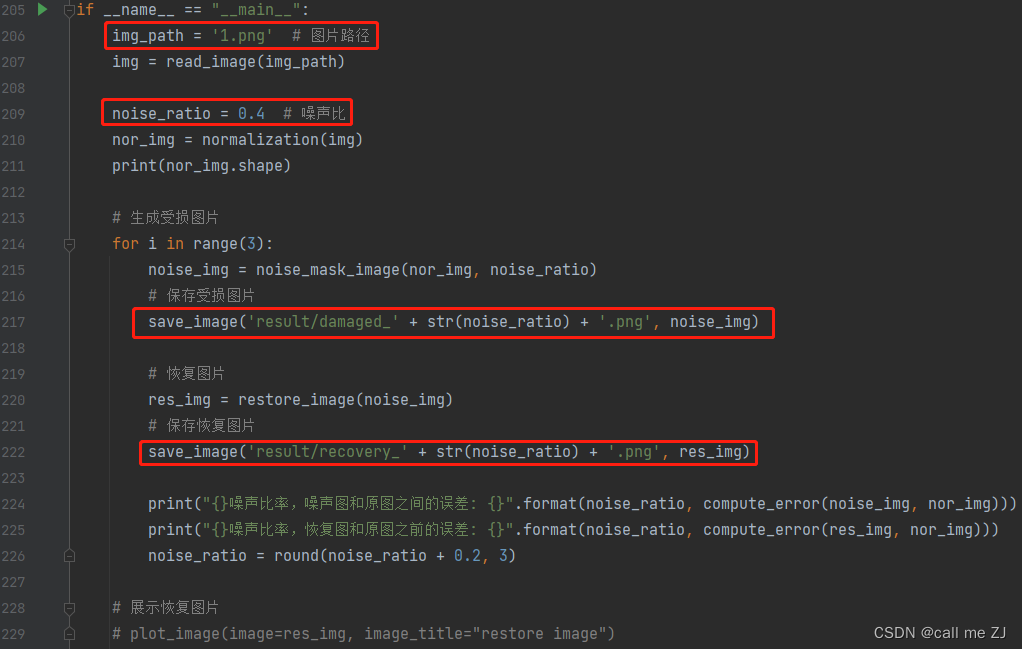
总共4个地方需要改,根据你自己环境
第一个地方你图像的路径
第二个噪声比,这个可以不改,运行代码会依次生成0.4,0.6,0.8受损比例的图片
第三个为生成受损图片的保存路径
第四个为恢复图片的保存路径
注意:这里代码都写固定了,如果没能力就别乱改,你只需要改好路径,运行即可,很容易上手
5.实验结果
将路径改好后运行代码,会在result文件夹中生成6张图片,受损3张比例(0.4,0.6,0.8)图片,以及对应比例的恢复图3张

原图

受损图片,从左到右依次(0.4,0.6,0.8)

恢复图片,从左到右依次(0.4,0.6,0.8)

6.结束语
到这里实验就结束了,还是很简单的一个小实验
这里代码参考自一篇博客,但我进行了一些改进,让代码使用起来更加方便上手
https://blog.csdn.net/zhangpeterx/article/details/90262269