早点关注我,精彩不错过!
(德国队出现形势分析在文末,可直接跳转。)
北京时间今天晚上11点整,如火如荼的卡塔尔世界杯就将展开小组赛第三轮比赛的争夺,8个小组轮番同时进行最后一轮较量,以决定出线权,以及淘汰赛中的对阵排列。
比起淘汰赛阶段win or go home的紧张刺激,世界杯的小组赛更像是一场亮相和狂欢,没有一场定胜负。但世界杯不是联赛,采用的是4队一组的单循环赛制。3场小组赛的每一场,甚至是每一个进失球,都关乎着后面所有的命运。
每当小组赛进行到最后阶段,各路媒体评论员们,就开始展望这个小组的出线形势。看起来很简单的就6场比赛的积分结果,却总能呈现出很复杂的局面。有时评论员的评价有可能片面,或者球迷也难以在短时间内摸清这里面本质的博弈关系,影响对比赛走势的判断和球迷的财路。
借着马上到来的小组赛最后一轮开打的东风,我决定再死理性派一把,研究清楚:作为4进2的世界杯小组赛阶段,一共可能出现哪些局面;在各局面下,各队伍的策略目标到底是什么呢?
希望我的研究成果能祝您世界杯观赛一臂之力!
世界杯小组赛的博弈模型
竞技体育除了田径是挑战自己以外,几乎都可以归为博弈项目。即有多个智能体参与者,各自有其效用函数希望最大化,而最终的效用结果是所有人策略的函数。数学里用博弈论来研究它们,用博弈模型对它进行建模和分析。
下面对世界杯小组赛阶段一个小组的4支队伍的博弈过程建模:
参与者:
每个小组的4支队伍,编号为1, 2, 3, 4。
博弈过程:
按官方公布的赛程安排,每个小组一共有3轮次,6场次的比赛。不失一般性,不妨设为:
第一轮:1 vs 2, 3 vs 4;
第二轮:1 vs 3, 2 vs 4;
第三轮:1 vs 4, 2 vs 3;
注:赛程设计只要符合照每轮每队都有出战,最终完成循环的要求即可。这里取队伍编号数值mod4的距离为1, 2, 3的队伍在每轮交战而设计。因队伍编号的对称性,这不失一般性,符合存在的赛程安排的规律。
于是,仅考虑到每场比赛的比分结果的粒度,整个小组赛博弈过程要经历6个局势和5次局势变化。设初始局势状态(以下简称局势)为S0,其中前两轮的4场依次进行,得到4个不同局势S1:4,后两场同时进行后得到的局势S5为终局。每轮每场比赛记录双方的进球数,红黄牌信息,以累积计算为当前局势;
效用目标函数:每支队伍都进行完3轮6场比赛后进入终局S5,都希望得到最佳的出线局面。假设所有队伍都依次优先考虑如下几方面的终局收益:
1. 能在指定的积分等排名规则中排前两名出线;
2. 能选择最有利自己的出线位置;
3. 能让敌对的球队不出线或处于不利赛程的出线位置;
注:出线排名规则:
依次看如下指标,有相同者继续在相同的队伍内看下一个指标:
1. 积分(胜3,平1,负0)
2. 总净胜球数
3. 总进球数
4. 胜负关系
5. 净胜球数
6. 总进球数
7. 公平比赛积分(黄1,二黄变一红3,红4,黄+红5,所有场次和队员累加)
8. 抽签
假设:
1. 不分析一个场次内达成某局势的足球策略和能否达成,仅分析在某局势下往前一步的最优局势;
2. 小组赛局势S4到S5时,同时进行的最后一轮的两场比赛的博弈过程为非完美信息博弈,两个场地的球员在赛场中不能通信商量和知道比赛局势,并且同时开始同时结束;
3. 在前两轮4场比赛中,所有球队的唯一策略目标都是全力争胜争平的胜负结果,以力保小组出线,而不考虑最优排名和做掉其他对手的情况;(实际上可能还存在净胜球,进球数和红黄牌数的考虑,但都在该策略目标达成以后,也并不直接矛盾,由此简化对实战策略影响,予以忽略)
4. 一场比赛内因为进球状态有先后,不存在互送进球数的策略,因为没有第三方保证它的顺利进行;
注:假设3成立的一个直观原因是:没有球队可以在第二轮自己的比赛开始前确保小组出线。因此在此轮之前,模糊的策略就是优先获得胜场积分以挤占排序优势位置为最重要的策略。除非对后面对手的策略和自己的排名目标有很清晰的预判,此时考虑别的因素是不值得的。
证明:没有球队可以在第二轮自己的比赛开始前确保小组出线。
第一轮比赛还没踢,如果全负必然不能出线,下面考虑第二轮。因为在第二轮开始之前,第3场比赛准备开赛之前的S2状态下,最好的情况是战胜对手积3分,而后面比赛如果全败而且净胜球最差时(倒不一定要求是最坏的情况,存在即可),那么其踢输的两支球队积分就都不低于他,故无法确保小组出线。(放缩法估算)
由假设3,因为前两轮4场比赛策略目标固定,任何局势对球队比赛结果的策略目标没有影响。故我们可以直接分析在给定了前两轮局势情况下,即第三轮同时比赛开始前的局势S4,包括可能的局势以及最终局势,和它们之间的连接关系,由此分析各队当时的策略目标和出线形势。又由假设4,此时局势仅仅和胜负关系有关,故以下仅分析胜负场次局势,其他比分和红黄牌局势在需要时候再分解分析。
我会把所有的分析结果清晰地贴在下方并附上使用方法和案例。相信我,有了这个表,再也不用头疼地听解说员分析半天“如果德国队XXX了,那日本队就XXX,但是若德国队不配合XXX,那么西班牙队XXX”,这个级别的内容真的不适合用自然语言描述,还得上数学结构。
第一轮比赛结束时的积分局势S2
第一轮比赛4支队伍都会亮相,捉对进行比赛。故局势比较简单,一共有以下3种情况:

其中,局势按照此时打平的场次分类,标注在左上角,队伍编号为1~4,“—”表示打平,→所指向的一方为胜者,源头为负者。
这个局面还比较简单,因为一共也就4支队伍,2场比赛,每队一场,枚举一下平的场次就想出来了,它关于任意队伍排列对称,队伍编号排列取得是顺时针转一圈的1~4作为代表编号,代表场次取得是上下两场(1vs2,4vs3)的结果排列的最小值,依次比较排列结果里的胜负关系,负 < 平 < 胜。
第二轮比赛结束时的积分局势S4
到第二轮结束,总共4场比赛进行,根据每轮每队都有出战,最终完成循环的要求容易证明,此时的比赛对阵结构是一个满足D4对称性的正方形,于是,我仍然取1~4的队伍编号顺时针转一圈作为队伍编号的代表排列,完成的4场比赛的对阵双方恰好对应正方形的4条边,分别为:
vertex_tuple = (1vs2, 2vs3, 3vs4, 4vs1)。
由假设3,我们不用分析S2 -> S4中各队的策略目标,因为此时都是全力争胜和平。故直接给出局势S4下的所有可能局面,为接下来的分析作准备:
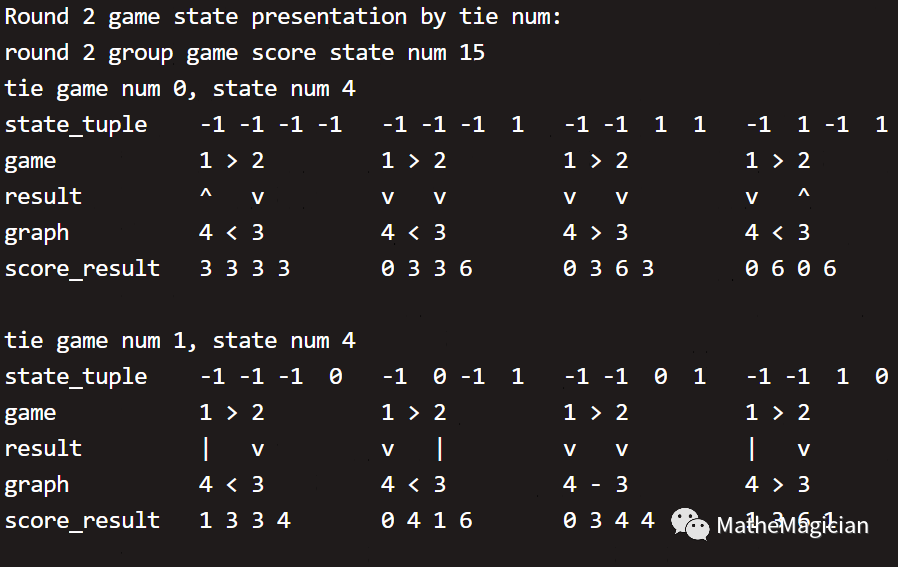
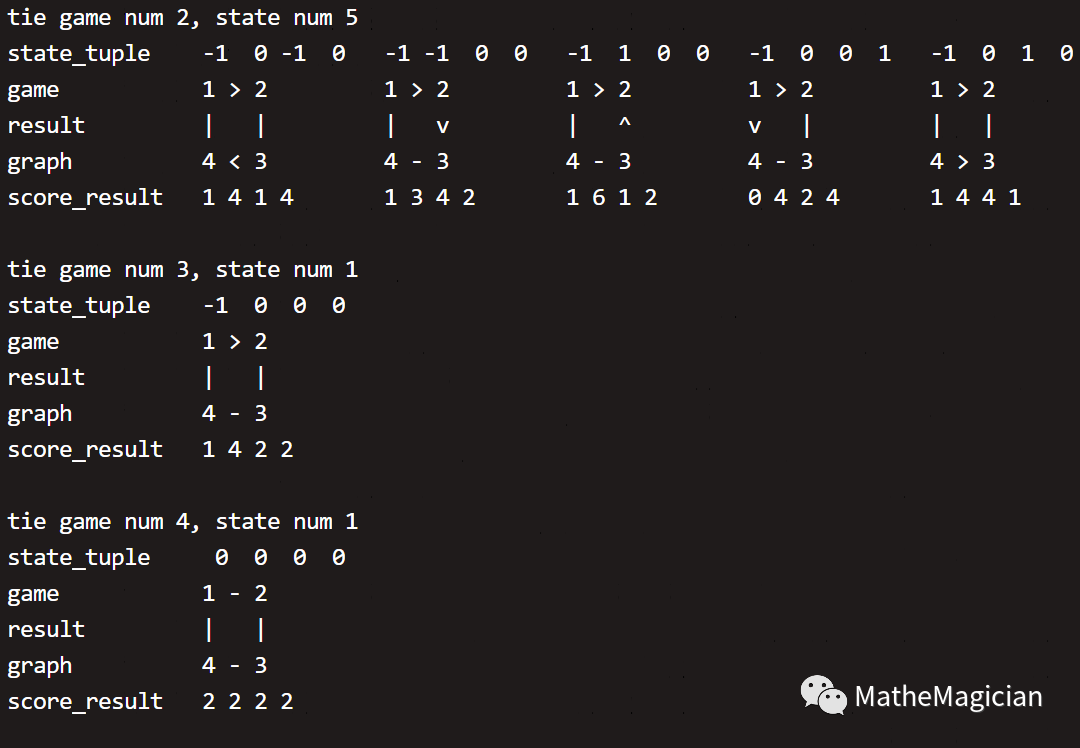
局势一共有15种(15个等价类,对应3 ^ 4 = 81种比赛结果元素),按照平局的数量0~4进行分类,state_tuple为vertex_tuple中设定的对战双方的比赛结果,- 1表示前者负,1表示胜,0表示平。应用ascii码把所有可能的非对称局势全都画了下来,“—”表示打平,→所指向的一方为胜者,源头为负者,取的是所有对称局势中state_tuple值最小的那一个。而根据D4群的结构,其上的所有操作对局势的改变都是等价局势。
怎么样,快来对照一下,你关心的小组,2轮比赛过后,处于上面哪一种局势,而你关心的队伍,又等价于哪一个编号呢?
小组赛终局积分局势S5
激动人心的终局,来了,如果说·S4的局面还相对简单,耐心一下用手算也能画出来不重不漏,但是到局势S5,4支队伍两两之间都进行了比赛,这里总比赛可能结果数为3 ^ 6 = 729种,那对称的等价局势有多少种呢?
注意了,因为两两之间都有边连接,此时队伍之间的对战关系是一个全排解对称的S4结构,这也符合预期,所有比赛打完,应该所人的赛程都应该是对称而公平的。如果把队伍看作定点,对战关系看作边,这就是一个三棱锥了,但是三棱锥的对称性是A4,那是因为刚体无法进行镜面变换,但是足球小组赛终局的对战关系可以!
要手绘这个三棱锥结构实在太麻烦,用ascii码表达的难度也不小,于是我设置代表对阵排列为:
vertex_tuple = (1vs2, 1vs3, 1vs4, 2vs3, 2vs4, 3vs4)
于是用一个6元的state_tuple就可以表达所有场次的胜负关系了,仍然是对靠前的队伍,- 1表示前者负,1表示胜,0表示平。全部结果如下(仍然按照平局数量分类):
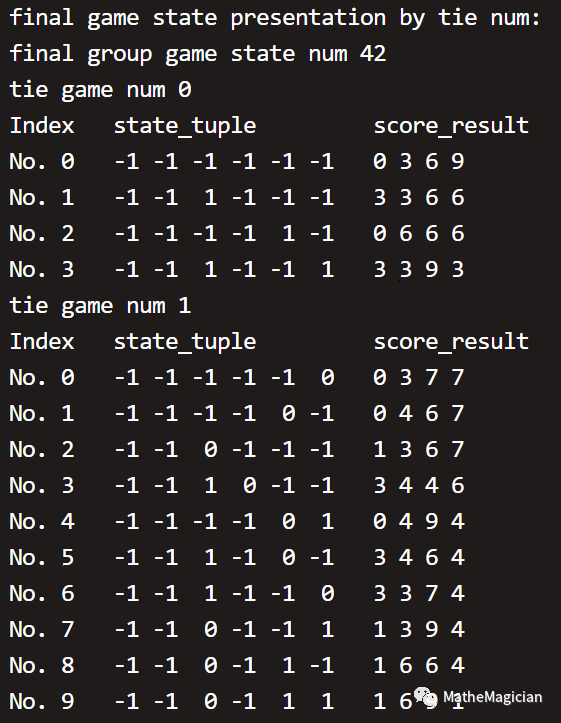
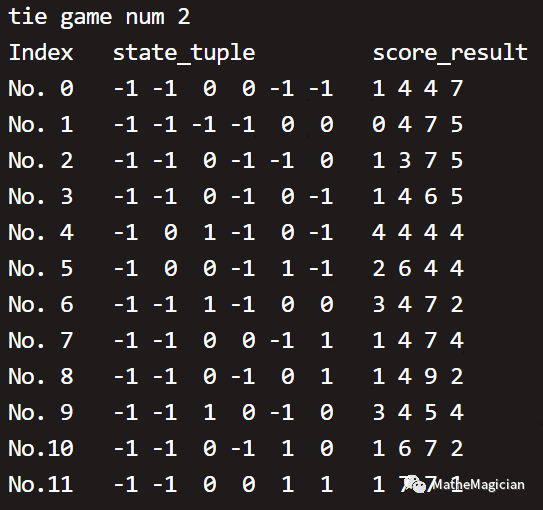
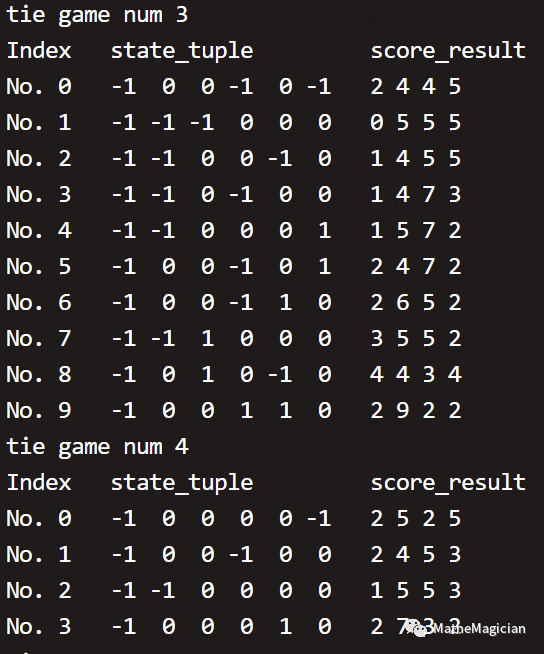
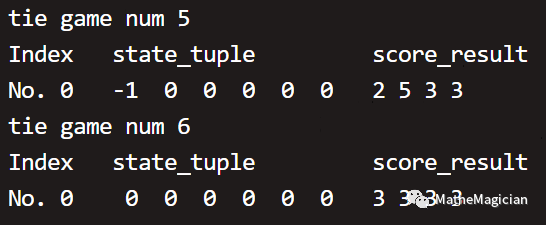
小组赛的终局一共有42种不同的胜负关系局势。如果你仔细看其中的局势和最后的积分情况,你会发现,很多以前让你困扰的小组赛出线问题,都迎刃而解了。
比如:最少积几分有可能小组出线?最少积积分一定能小组出线?
这么简单的问题我就不回答了,大家自己去图片里捉虫。
另外还有一个有意思的点,就是,积分顺序排列相同的两个比赛结果局势一定相同吗?
以前拿着脑筋想破天际也想不出来,那是因为大脑在一些规模庞大的问题上真的毫无章法,这里直接就可以跑出答案:
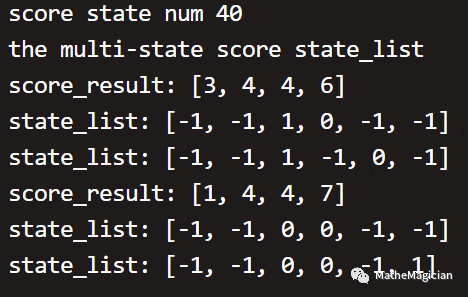
如果按照积分的顺序排列作为积分局势,一共是40种,其中有两种里面存在多种比赛结果局势,有兴趣的同学可以画出对应的三棱锥或者带对角线的正方形比赛结果图来分析异同。
从第二轮局势S4到终局S5的博弈积分表
有了上面的铺垫,我们终于可以回答那个问题了:德国队在最后一轮中的出线形势到底如何?
我们把S4中的每一种局势下,在第三轮比赛中的3 * 3共9种最后一轮的策略目标下的终局积分全部画了出来:
(state_list是S4时的比赛结果局势,score_list是积分局势,每行是1vs3对阵的结果,每列是2vs4对阵的结果,表中值为最终的积分局势,括号内为形成的终局对应的在S6终局分析中的那40种终局的平局数和编号,其中需要进行队伍的再排列才能对上,但是是等价的局势)
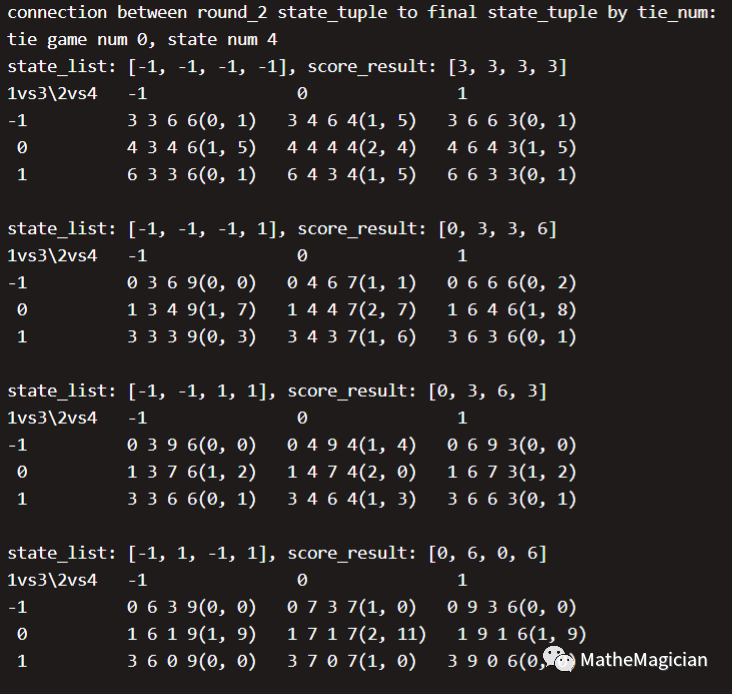
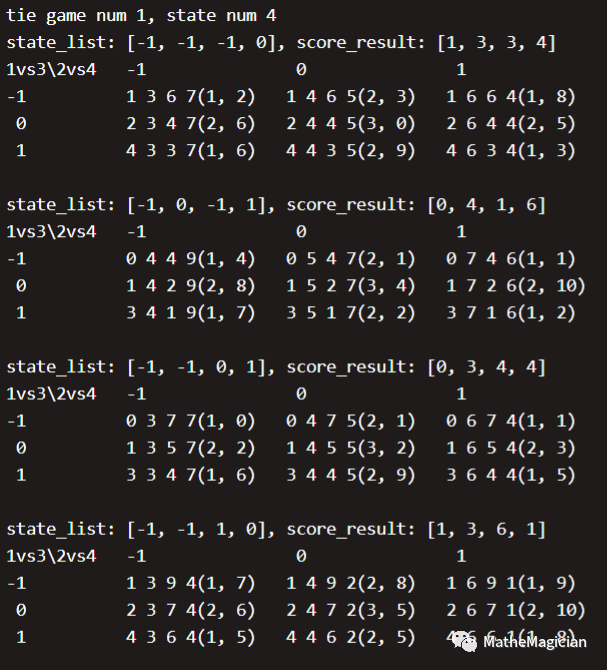
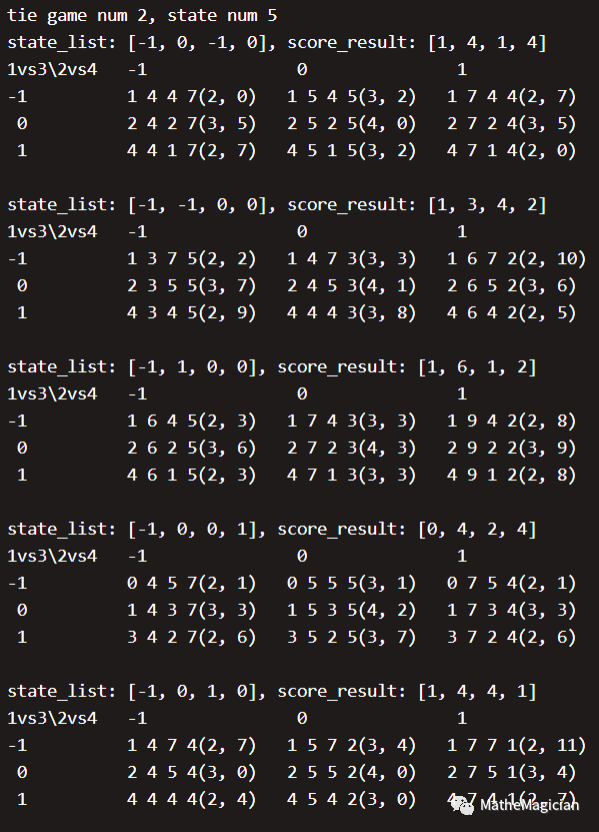
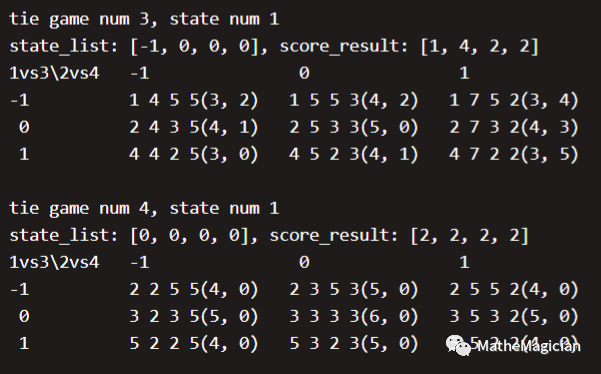
表德国队的出线形势如何?有没有可能被西班牙做掉?
有了这个强大的赛局分析工具,那我们想分析小组赛最后一轮的出线形势就一目了然了。
注意,根据出线规则,大量积分打平的情况下需要比进球数,红黄牌等因素,当把主要问题解决以后就可以来具体看案例中的进球和红黄牌因素;同时可以开始考虑每队除了出线以外的其他如位次和干掉其他对手的目标了(这里存在一个不公平因素是,每个小组的终局到达时间不同,因此越晚的比赛的小组越能够获得挑选后期对手的后手优势)。另外,这其中也可以充分运用纯策略下的完全不完美的双人博弈模型的均衡策略分析方法,来具体分析每队的出线形势,以及有没有可能因为特殊局势导致一些有趣的默契球等情况的发生,十分有意思。
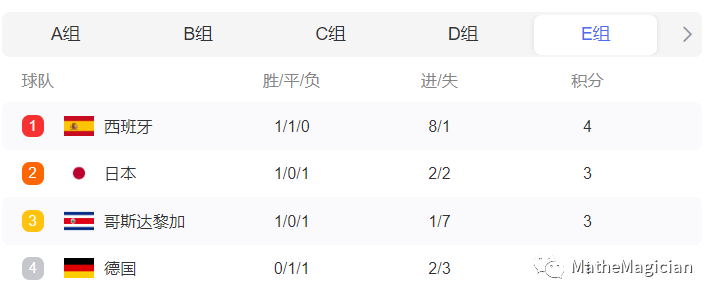
下面以E组S4局势时的出线形势分析为例,来讲解一下本表的使用方法。下面是对阵的积分结果图:
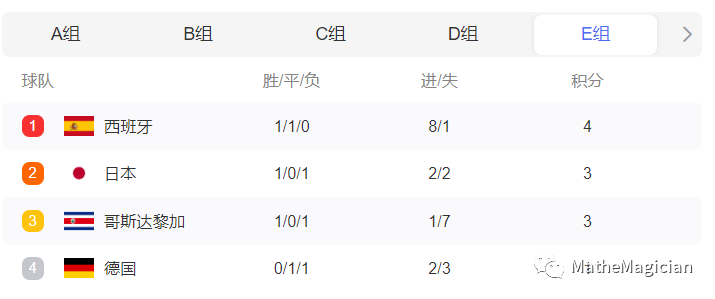
根据前两轮的对阵结果数据,很容易分析出,其S4局势如下图所示:

其中1~4分别为1:德国(- 1,2);2:日本(0,2);3:哥斯达黎加(- 6,1);4:西班牙(7,8),括号中为净胜球和进球数。
拿出此时的局势转移图:

行的1vs3即为:德国vs哥斯达黎加,列的2vs4为:日本vs西班牙。
先来看1德国队。如果输球(表中第1行)必定因为积分出局;如果打平也同理;如果赢球,只有在日本也输球的情况下能确保以小组第二晋级;如果日本打平则需要互相比净胜球等进入后面的比较;而日本赢球的话,需要和西班牙比净胜球等决定晋级。
因为西班牙曾经7:0哥斯达黎加,净胜球的优势巨大,因此最后一种情况大概率淘汰;而日本打平则净胜球仍然为0,则德国需要2+个净胜球才能确保出线,而2个净胜球时,就要看双方最后一场的进球数比,再相同则日本凭借胜负关系晋级。
综合以上,德国必须全力争胜的同时保证2+个净胜球或足够多的进球数,为其唯一dominating的策略目标,根据效用函数假设,不太存在放弃赢球而考虑做掉其他球队的可能。
再来看2日本队。如果输球(表中第1列),无论其他结果如何,必不能出线;如果打平,则在德国输球的情况下必不能出线;德国打平时需要和哥斯达黎加比进球数争小组第二,德国打赢则要比净胜球等;赢球则必出线,且只有德国输球时要和哥斯达黎加比净胜球,其余都是小组第一。
故日本赢球为dominating策略,打平则要争取最多的进球数,没有做球可能。
接着看3哥斯达黎加。赢球必出线,如果日本队也赢,则要比净胜球争小组第一,其他都是小足球第一;打平时只有日本输球时一定以小组第二出线,其他时候都需要比较净胜球等争小组第二;输球时必不能出线。
故哥斯达黎加赢球为dominating策略,打平时再争取更多进球数,没有做球可能。
最后看4西班牙。赢球必然小组第一出线,打平只有在德国输球的时候为小组第二,其他情况为小组第一,输球时若德国队输球则不能出线,否则要比净胜球以小组第二出线。
故输球为西班牙的dominated策略,需要避免,而在确保出线的情况下,如果分析表明,小组第二的后续淘汰赛程更有利(在部分已知前面其他组出线结果和形势的条件下),那西班牙存在小概率为了打平而加强防守,以获得一丝小组第二的机会。那德国虽然会导致一定不能出线,但就会更加义无反顾地争胜来破坏西班牙的策略目标,即效用函数的第三级别,破坏有仇的对手,而且这也与自身的出线第一目标不矛盾。
而且要知道,默契打平是一件十分困难的事,根据假设4,没有人会在场内这样冒险。因此,整体而言,西班牙依然不会选择做球,而是争胜。
综上,德国没有被西班牙做掉的风险,所有球队都会全力争胜争平以确保最有利的出线形势。
下期再会!
当然,并不是每种局势下都完全不存在默契球的,大家不妨用我给的数据表对照着分析一下其他你感兴趣的小组和球队,看看他们的出线形势如何,有没有特殊的违背常识的有趣策略发生。
好了,以上就是今天的全部内容。因为世界杯的到来让我重启了一个数学问题的思考,并把结果送给大家应该是我最开心的事了。因时间关系,本文重点呈现世界本小组赛最后一轮的形势分析方法的实操结果。关于这个计算这个组合的过程中还有很多值得挖掘的数学,计算机等更多思考感悟,还有对这个结果的进一步分析和探讨,我会在接下来的系列中在整理好给大家呈现,不见不散!
祝你在整个世界杯期间都能预测未来!

我们是谁:
MatheMagician,中文“数学魔术师”,原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义,也取像魔术一样玩数学的意思。文章内容涵盖互联网,计算机,统计,算法,NLP等前沿的数学及应用领域;也包括魔术思想,流程鉴赏等魔术内容;以及结合二者的数学魔术分享,还有一些思辨性的谈天说地的随笔。希望你能和我一起,既能感性思考又保持理性思维,享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流!


扫描二维码
关注更多精彩
我的数学学习回忆录——一个数学爱好者的反思(一)
纠错码与魔术(四)——汉明纠错码魔术进阶
破解魔术的秘密(四)——前移原理介绍和案例分享
你真的分得清“前后左右”和“东西南北”吗?(四)——无处不在的相对方位
编码通信与魔术初步(七)——二进制编码经典魔术《街头猜数字》

点击阅读原文,往期精彩不错过!