目录

动态规划之禅

多种纬度解决Fibonacci 数列

什么是Fibonacci数列

朴素递归方案

朴素递归的问题

Fib自上而下、备忘录方案

Fib自下而上法

---

动态规划之禅

动态规划是算法基础部分中最有趣的一个了，我想了很多天，怎么用很短的一些话把动态规划像之前的算法总结一样给大家总结出来，然后再给一些题目出来让大家练习以融会贯通彻底拿下这个知识。

然后发现和贪心策略一样，动态规划不是一种固定的套路，而是一种思想：【用过去的积累解决现在的问题】，我把这个思想叫做动态规划之禅。

多种纬度解决Fibonacci 数列

什么是Fibonacci数列

用一串数字可以对Fibonacci进行归纳：

1，1，2，3，5，8，....,num[n-1],num[n],num[n-1]+num[n]

下面是它的递归结构，即num[n] = num[n-1] + num[n-2] if n >= 2

朴素递归方案

我们利用这个规律可以用非常朴实的方法做一个程序去计算第N个值的大小：

int fib(int n) {
    if(n<=0) return 0;
    if(n<=2) return 1;
    return fib(n-1) +fib(n-2);
   
}

下面是这个程序的执行结构：

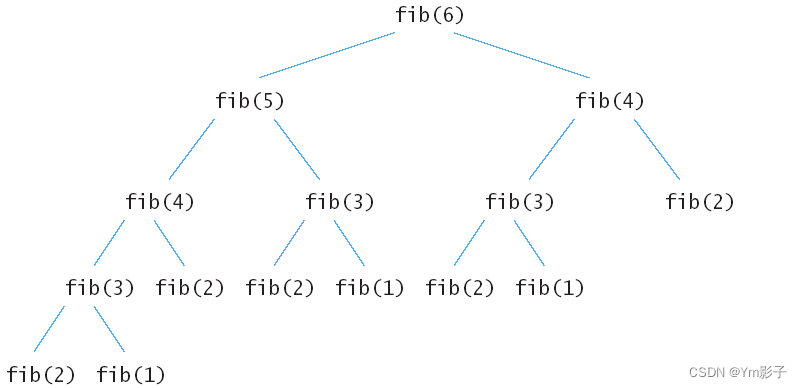
 我们把一个规模为N 的问题分解为两个规模为N-1 、N-2 的问题，然后不断的分下去，直到问题变成一个已解的问题，比如 落到 fib（1）、fib（2）上。

朴素递归的问题

然后我们实际去执行这段代码的时候就会发现一旦我们求的值变大了之后，计算需要的时间会变的非常大！这和我们的时间复杂度是有关的，不难看出上面那颗树，如果每一个节点都代表我们要计算一次，那么我们需要计算2^（n -1）次。

我们需要研究一下这个树存在的问题是什么，很明显重复计算太多了，每求一个fib(x)，都要把值一直回溯到fib（1）、fib（2），那有没有办法把之前已经计算好的值直接拿来用呢？而不是再重新计算一次。

Fib自上而下、备忘录方案

这次我们在算法开始之前先申请一个大小为N 的空间, 这段空间用于记录计算过的值，之后再次用到的时候，直接使用cache空间中的值，而不是去重新计算。

cache有些类似我们平时使用的备忘录，计算也是自上而下的，所以这种方法也叫自上而下法或者备忘录法。

代码如下：

int _fib(int n, int* cache) {
   if(n<=0) return 0;
   if(n<=2) return 1;
   int num1 = 0;
   int num2 = 0;
   if(cache[n-1] != -1) {
    num1  = cache[n-1];
   }
   else {
    num1 = _fib(n-1);
    cache[n-1] = num1;
   }
   if(cache[n-2] !=-1)
   {
    num2 = cache[n-2];
   }
   else {
    num2 = _fib(n-2);
    cache[n-2] = num2;
   }
   return num1 + num2;

}
int fib(int n) {
    int *cache = (int*)malloc(sizeof(int)*n);
    for(int i =0;i<n;i++) {
        cache[i] = -1;
    }
    return _fib(n, cache);
    
}

Fib自下而上法

因为Fibonacci 是小规模已知的，且更大的规模可以都是基于fib（1）、fib（2）求得的，因此可以使用自下而上法来实现。

即求fib（n），就从fib（1）+fib（2）算出fib（3），再从fib（2）+ fib（3），求得fib（4），一直求到fib（n）。

下面是代码：

int fib(int n) {
    if (n<=0) return 0;
    if (n<=2) return 1;
    int num1 = 1;
    int num2 = 1;
    for(int i = 2;i<n;i++) {
       int tmp = num1+num2;
       num1 = num2;
       num2 = tmp;
    }
    return num2;
}