文章目录
- 一、归并排序递归法
- 1.归并排序的基本思想
- 2.归并排序的代码实现
- 二、归并排序非递归
- 1.可否使用栈来模拟?
- 2.直接改非递归(简化版)
- 3.处理边界之一把梭哈
- 4.处理边界之归并一次拷贝一次
一、归并排序递归法
1.归并排序的基本思想
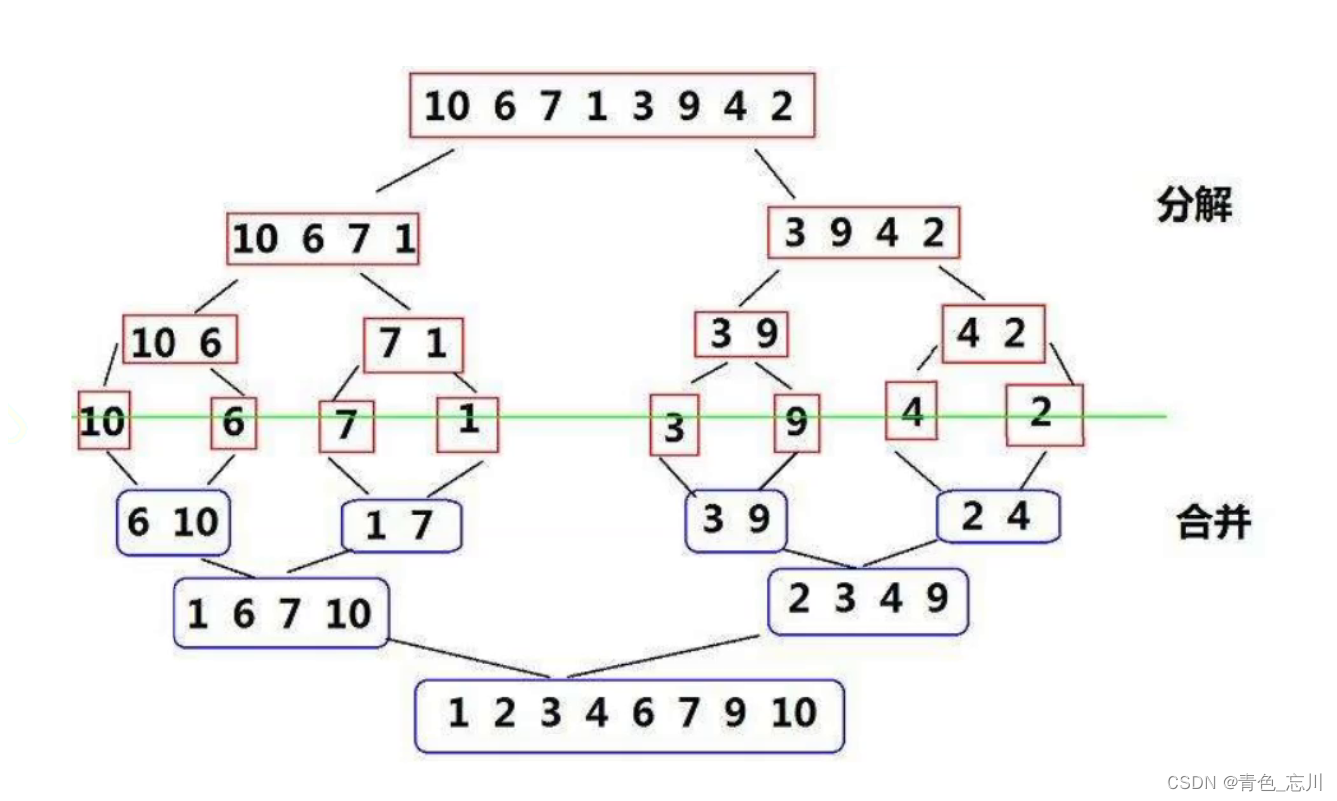
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
也就是说,先将排序给劈成两半,然后对分别对左边和右边使用归并使得左右都变得有序。然后我们在对左右子数组进行归并即可
2.归并排序的代码实现
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end)
{
return;
}
int mid = (begin + end) / 2;
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
//归并排序
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
return 0;
}
二、归并排序非递归
1.可否使用栈来模拟?
其实是不可以的,因为这里类似于一个后序遍历,而快排之所以可以使用栈来模拟,是因为他是一个先序遍历。
对于快速排序,他是一趟搞定一个,当递归结束而不返回的时候,已经排好了。
而对于归并排序,他是先搞左右两边的。最后还需要获取原来的区间的。显然栈无法实现这样的功能。
2.直接改非递归(简化版)
我们可以这样思考,如果我们利用循环,先将前一个元素认为是一组给归并,然后依次归并后,再将两个元素设置为一组依次归并。让每组元素个数依次乘以2。只要起始值不越界。就可以一直依次拷贝下去。我们可以这样做,但是这种方式存在一个很明显的问题。只可以归并前2的次方的数组。否则将会产生越界的风险
//归并排序非递归
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int j = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
}
gap *= 2;
memcpy(a, tmp, sizeof(int) * n);
}
free(tmp);
}
3.处理边界之一把梭哈
我们有了上面的代码作为基础,我们发现上面存在的问题是会出现越界。需要注意的是,在上面的代码中,我们并不是跟递归一样。每处理一组拷贝一组,我们是处理一次间距后才进行拷贝,也就是一把梭哈的。这就会出现一些潜在的问题。
为了处理边界问题,我们不妨先将代码的可能出现的越界情况给分析出来
我们一共有九个元素,不难发现,除了begin1之外都有可能产生越界
为了方便我们分析,我们将上面的情况分为三类
1.end1越界,此时我们直接不归并就可以了。但是需要注意的是,我们是一把梭哈的,所以我们还是需要将[begin1,n-1]这段区间给拷贝下去。否则出现问题。为了拷贝给tmp,我们可以这样做,修正end1为n-1,然后将beigin2和end2给搞成不存在的区间
2.end1不越界,但begin2越界。这样的话,我们只需要将begin2和end2所控制的区间给不存在即可。
3.end1,begin2不越界,但end2越界。这样的话,我们就直接将end2给修正为n-2即可
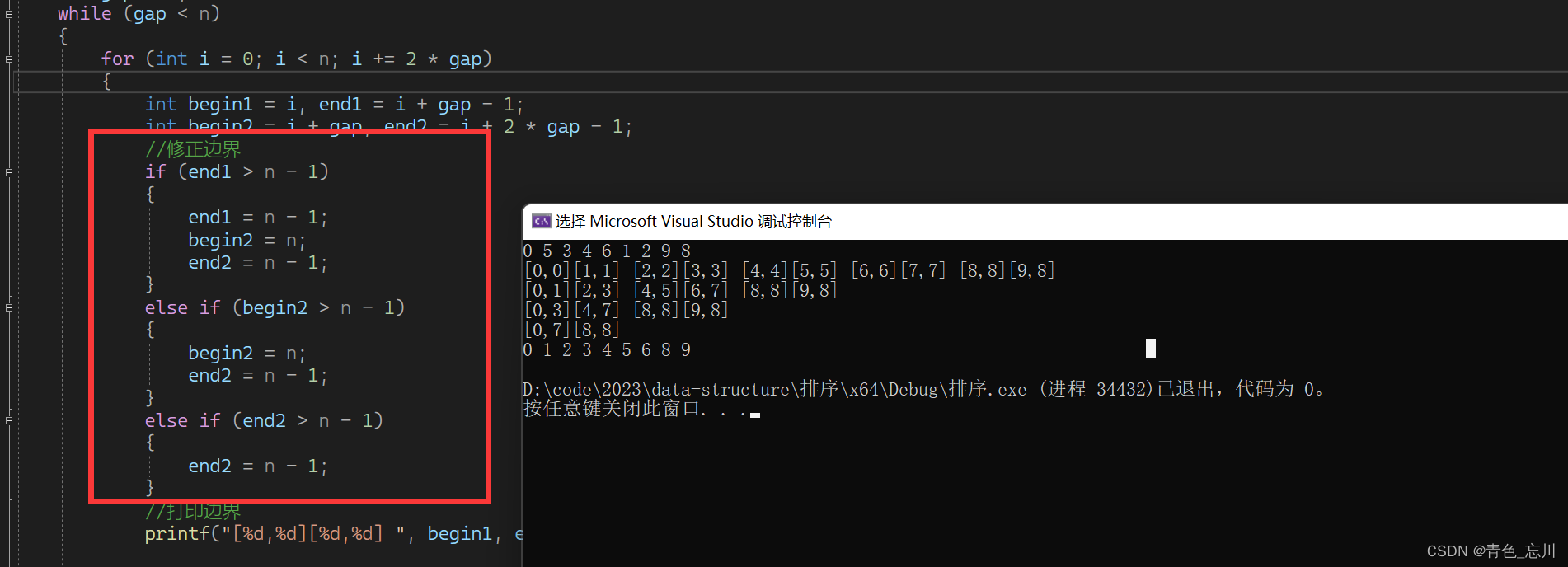
结果如下所示,这样一来我们就成功的修正了边界
代码如下:
//归并排序非递归
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//修正边界
if (end1 > n - 1)
{
end1 = n - 1;
begin2 = n;
end2 = n - 1;
}
else if (begin2 > n - 1)
{
begin2 = n;
end2 = n - 1;
}
else if (end2 > n - 1)
{
end2 = n - 1;
}
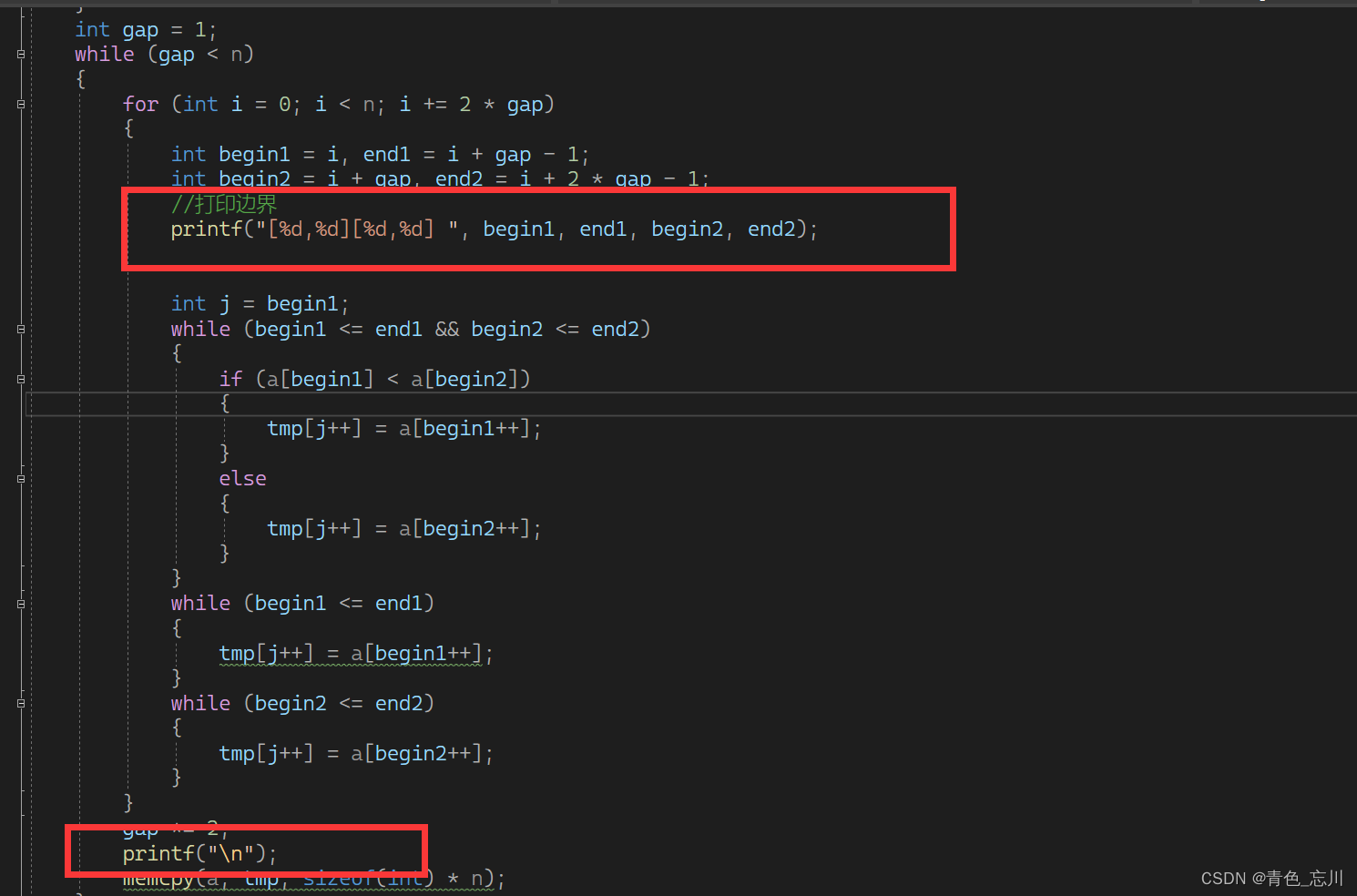
//打印边界
//printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);
int j = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
}
gap *= 2;
//printf("\n");
memcpy(a, tmp, sizeof(int) * n);
}
free(tmp);
}
4.处理边界之归并一次拷贝一次
这样的话,我们就可以简化很多了。我们对于end1越界和begin1越界,我们直接break就可以了。唯一需要注意的是拷贝的元素个数是end2-i+1,因为i是起始位置下标,end2是末位置。
//归并排序非递归
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//修正边界
if (end1 > n - 1 || begin2 > n - 1)
{
break;
}
else if (end2 > n - 1)
{
end2 = n - 1;
}
printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);
int j = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2;
printf("\n");
}
free(tmp);
}
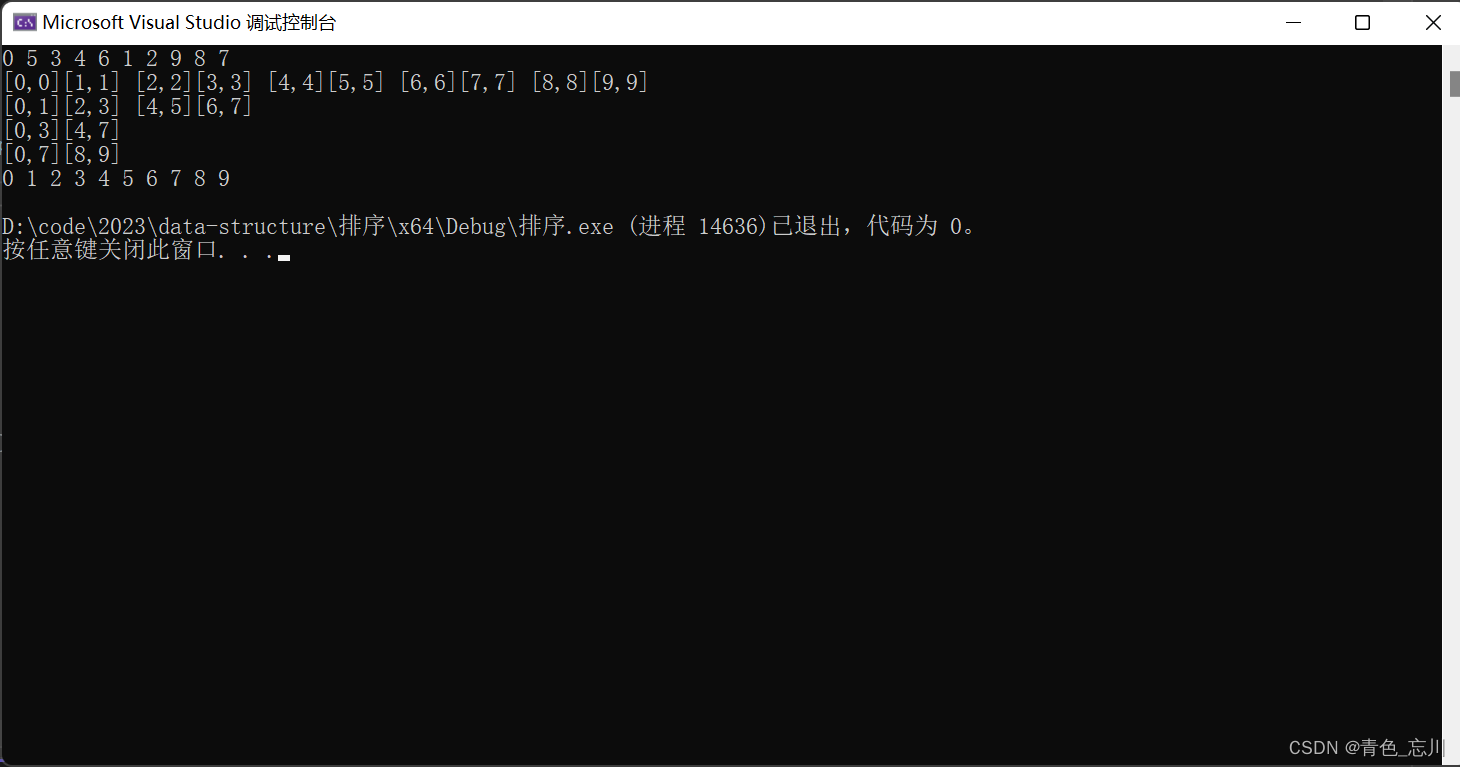
打印结果为
我们可以发现,对于不符合区间的部分,我们就直接不管这块的区间了
本期内容到此位置
如果对你有帮助的话,不要忘记点赞加收藏哦!!!








-软件测试背景、软件开发过程、软件测试基础](https://img-blog.csdnimg.cn/79677cf37f0e41febc033115d7aa0ebf.png#pic_center)

![[创新工具和方法论]-02- DOE实验设计步骤](https://img-blog.csdnimg.cn/img_convert/957a894034fa06407e058325031ca946.png)