一.跳跃游戏简单介绍
1. 跳跃游戏简单介绍
跳跃游戏是一种典型的算法题目,经常是给定一数组arr,从数组的某一位置i出发,根据一定的跳跃规则,比如从i位置能跳arr[i]步,或者小于arr[i]步,或者固定步数,直到到达某一位置,可能是数组的最后一个位置,也有可能是某一特别的数值处,也有可能在这个过程中,可能需要求解可能存在的最大值或者最小值。
对于跳跃游戏类的题目,经常使用贪心、动态规划、dfs、bfs等方法解决,对于可以使用dfs解决的题目,经常也可以使用动态规划,但一般贪心可以有更好的时间复杂度和空间复杂度。还有经常使用的动态规划剪枝、前缀和、滑动窗口和BFS,由于在大部分情况下,能用DFS解决的题目都可以用BFS解决,且两种方法有基本相同的复杂度,尤其是在跳跃游戏这类题目中,可以视为一种方法。
本文借青蛙酱主要复习动态规划三部曲。
2.跳跃游戏典型题目
(1)leetcode70 爬楼梯
(2)leetcode剑指 Offer 10- II. 青蛙跳台阶问题
(3)剑指 Offer II 088. 爬楼梯的最少成本
(4) leetcode55 跳跃游戏
(5)leetcode45 跳跃游戏 II
(6) leetcode1306 跳跃游戏 III
(7)leetcode1696 跳跃游戏 VI
(8)leetcode1871 跳跃游戏 VII
(9)leetcode1413 逐步求和得到正数的最小值
以上部分,请见:
跳跃游戏 (贪心/动态规划/dfs)
跳跃游戏 (动态规划剪枝/前缀和/滑动窗口/BFS剪枝)
3.动态规划三步曲复习
Java-算法-动态规划
二.跳跃游戏相关专题-青蛙酱🐸的奇妙冒险
1. 剑指 Offer 10- II 青蛙跳台阶问题
见 一.2.(2)
2. leetcode 2498 青蛙过河 II
给你一个下标从 0 开始的整数数组 stones ,数组中的元素 严格递增 ,表示一条河中石头的位置。
一只青蛙一开始在第一块石头上,它想到达最后一块石头,然后回到第一块石头。同时每块石头 至多 到达 一次。
一次跳跃的 长度 是青蛙跳跃前和跳跃后所在两块石头之间的距离。
更正式的,如果青蛙从 stones[i] 跳到 stones[j] ,跳跃的长度为 |stones[i] - stones[j]| 。
一条路径的 代价 是这条路径里的 最大跳跃长度 。
请你返回这只青蛙的 最小代价 。

输入:stones = [0,2,5,6,7]
输出:5
解释:上图展示了一条最优路径。
这条路径的代价是 5 ,是这条路径中的最大跳跃长度。
无法得到一条代价小于 5 的路径,我们返回 5 。
输入:stones = [0,3,9]
输出:9
解释:
青蛙可以直接跳到最后一块石头,然后跳回第一块石头。
在这条路径中,每次跳跃长度都是 9 。所以路径代价是 max(9, 9) = 9 。
这是可行路径中的最小代价。
class Solution {
public int maxJump(int[] stones) {
if(stones.length <= 2) return stones[1]-stones[0];
int ans = stones[2]-stones[0];
for(int i = 2; i < stones.length; i++) ans = Math.max(ans,stones[i]-stones[i-2]);
return ans;
}
}本题小结:
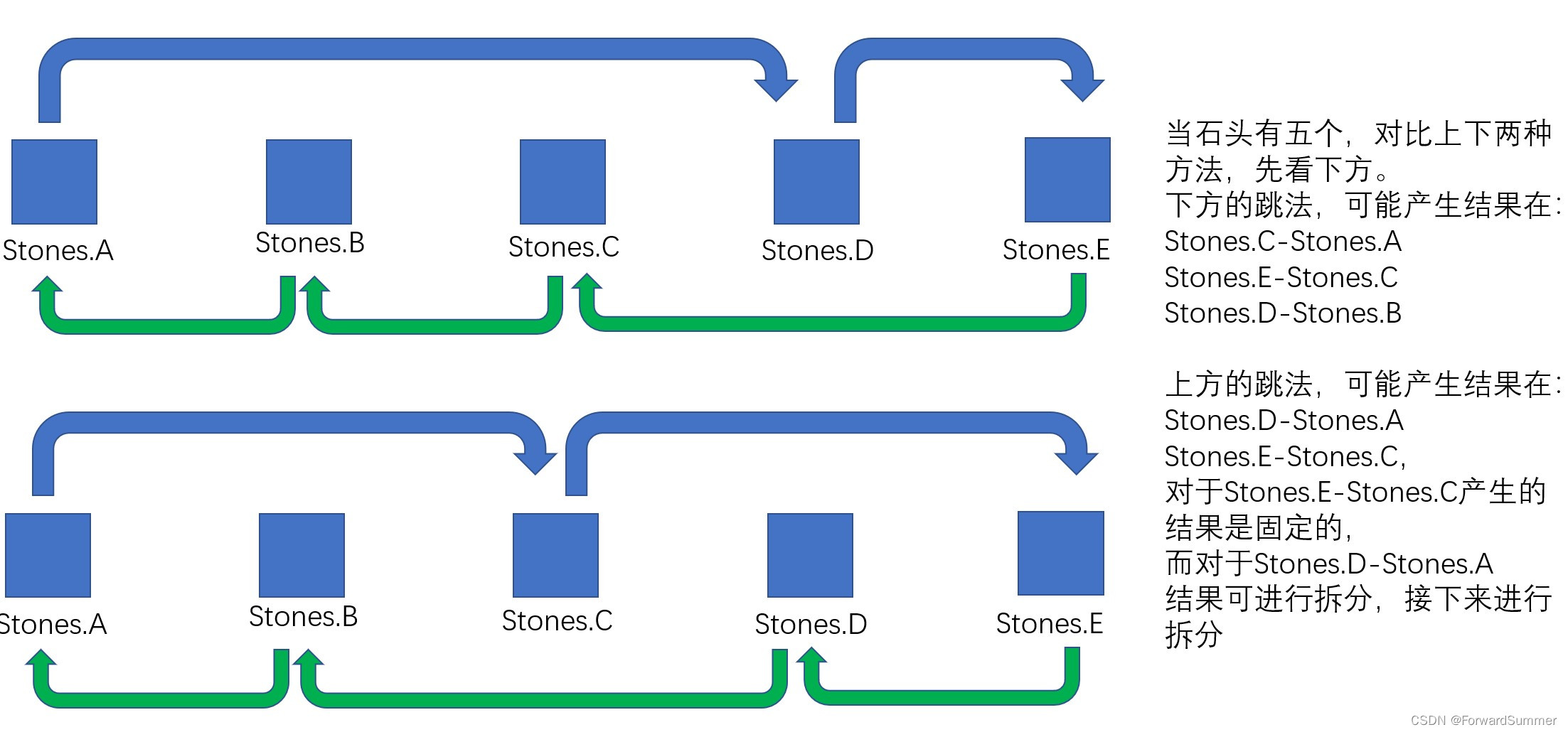
(1)首先思考,是跳所有的石头产生的结果最小还是漏过一些石头产生的结果最小,很显然,把所有的石头都跳过,在中间相当于插值,所产生的结果才有可能是最小的,即min(跳所有的石头)<=min(漏过一些石头)
(2)一句话贪心证明:大于三个的一段距离都可以进行分解成更小的段





3. leetcode 403. 青蛙过河
一只青蛙想要过河。 假定河流被等分为若干个单元格,并且在每一个单元格内都有可能放有一块石子(也有可能没有)。 青蛙可以跳上石子,但是不可以跳入水中。
给你石子的位置列表 stones(用单元格序号 升序 表示), 请判定青蛙能否成功过河(即能否在最后一步跳至最后一块石子上)。开始时, 青蛙默认已站在第一块石子上,并可以假定它第一步只能跳跃 1 个单位(即只能从单元格 1 跳至单元格 2 )。
如果青蛙上一步跳跃了 k 个单位,那么它接下来的跳跃距离只能选择为 k - 1、k 或 k + 1 个单位。 另请注意,青蛙只能向前方(终点的方向)跳跃。
输入:stones = [0,1,3,5,6,8,12,17]
输出:true
解释:青蛙可以成功过河,按照如下方案跳跃:跳 1 个单位到第 2 块石子,
然后跳 2 个单位到第 3 块石子, 接着 跳 2 个单位到第 4 块石子,
然后跳 3 个单位到第 6 块石子, 跳 4 个单位到第 7 块石子, 最后,
跳 5 个单位到第 8 个石子(即最后一块石子)。
输入:stones = [0,1,2,3,4,8,9,11]
输出:false
解释:这是因为第 5 和第 6 个石子之间的间距太大,没有可选的方案供青蛙跳跃过去。
DFS
class Solution {
int[] stones;
HashMap<Integer,Integer> map = new HashMap<>();
boolean flag = false;
public boolean canCross(int[] stones) {
this.stones = stones;
int len = stones.length;
if(stones[1] >= 2) return false;
for(int i =0; i < len; i++){
map.put(stones[i],i);
}
dfs(1,1,len);
return flag;
}
public void dfs(int index, int k, int len){
if(index == len-1){
flag = true;
return;
}
if(k == 1){
if(stones[index]+1 <= stones[len-1]){
if(map.containsKey(stones[index]+1)){
dfs(map.get(stones[index]+1),1,len);
}
}
if(stones[index]+2 <= stones[len-1]){
if(map.containsKey(stones[index]+2)){
dfs(map.get(stones[index]+2),2,len);
}
}
}
else{
if(stones[index]+k-1 <= stones[len-1]){
if(map.containsKey(stones[index]+k-1)){
dfs(map.get(stones[index]+k-1),k-1,len);
}
}
if(stones[index]+k <= stones[len-1]){
if(map.containsKey(stones[index]+k)){
dfs(map.get(stones[index]+k),k,len);
}
}
if(stones[index]+k+1 <= stones[len-1]){
if(map.containsKey(stones[index]+k+1)){
dfs(map.get(stones[index]+k+1),k+1,len);
}
}
}
}
}当然dfs是不能通过的
记忆化搜索
class Solution {
int[] stones;
HashMap<Integer,Integer> map = new HashMap<>();
boolean flag = false;
boolean[][] memo;
public boolean canCross(int[] stones) {
this.stones = stones;
int len = stones.length;
if(stones[1] >= 2) return false;
for(int i =0; i < len; i++){
map.put(stones[i],i);
}
memo = new boolean[len][len+1];
dfs(1,1,len);
return flag;
}
public void dfs(int index, int k, int len){
if(index == len-1){
flag = true;
return;
}
if(memo[index][k]) return;
if(k == 1){
if(map.containsKey(stones[index]+1)){
dfs(map.get(stones[index]+1),1,len);
}
if(map.containsKey(stones[index]+2)){
dfs(map.get(stones[index]+2),2,len);
}
}
else{
if(map.containsKey(stones[index]+k-1)){
dfs(map.get(stones[index]+k-1),k-1,len);
}
if(map.containsKey(stones[index]+k)){
dfs(map.get(stones[index]+k),k,len);
}
if(map.containsKey(stones[index]+k+1)){
dfs(map.get(stones[index]+k+1),k+1,len);
}
}
memo[index][k] = true;
}
}实际上以上的解法可以看出很多代码是可以重复的,可以写成for循环,堆结果合并,并处理k=1的特殊情况。
Ref.[1]:
DFS
class Solution {
Map<Integer, Integer> map = new HashMap<>();
public boolean canCross(int[] ss) {
int n = ss.length;
// 将石子信息存入哈希表
// 为了快速判断是否存在某块石子,以及快速查找某块石子所在下标
for (int i = 0; i < n; i++) {
map.put(ss[i], i);
}
// check first step
// 根据题意,第一步是固定经过步长 1 到达第一块石子(下标为 1)
if (!map.containsKey(1)) return false;
return dfs(ss, ss.length, 1, 1);
}
/**
* 判定是否能够跳到最后一块石子
* @param ss 石子列表【不变】
* @param n 石子列表长度【不变】
* @param u 当前所在的石子的下标
* @param k 上一次是经过多少步跳到当前位置的
* @return 是否能跳到最后一块石子
*/
boolean dfs(int[] ss, int n, int u, int k) {
if (u == n - 1) return true;
for (int i = -1; i <= 1; i++) {
// 如果是原地踏步的话,直接跳过
if (k + i == 0) continue;
// 下一步的石子理论编号
int next = ss[u] + k + i;
// 如果存在下一步的石子,则跳转到下一步石子,并 DFS 下去
if (map.containsKey(next)) {
boolean cur = dfs(ss, n, map.get(next), k + i);
if (cur) return true;
}
}
return false;
}
}
记忆化搜索
class Solution {
Map<Integer, Integer> map = new HashMap<>();
// int[][] cache = new int[2009][2009];
Map<String, Boolean> cache = new HashMap<>();
public boolean canCross(int[] ss) {
int n = ss.length;
for (int i = 0; i < n; i++) {
map.put(ss[i], i);
}
// check first step
if (!map.containsKey(1)) return false;
return dfs(ss, ss.length, 1, 1);
}
boolean dfs(int[] ss, int n, int u, int k) {
String key = u + "_" + k;
// if (cache[u][k] != 0) return cache[u][k] == 1;
if (cache.containsKey(key)) return cache.get(key);
if (u == n - 1) return true;
for (int i = -1; i <= 1; i++) {
if (k + i == 0) continue;
int next = ss[u] + k + i;
if (map.containsKey(next)) {
boolean cur = dfs(ss, n, map.get(next), k + i);
// cache[u][k] = cur ? 1 : -1;
cache.put(key, cur);
if (cur) return true;
}
}
// cache[u][k] = -1;
cache.put(key, false);
return false;
}
}以上四种解答,两种写法,在本质上一样,枚举在一个位置可能的情况,进行递归,DFS都不能通过,使用记忆化搜索降低时间复杂度,走过的路不再走。
动态规划
class Solution {
public boolean canCross(int[] ss) {
int n = ss.length;
// check first step
if (ss[1] != 1) return false;
boolean[][] f = new boolean[n + 1][n + 1];
f[1][1] = true;
for (int i = 2; i < n; i++) {
for (int j = 1; j < i; j++) {
int k = ss[i] - ss[j];
// 我们知道从位置 j 到位置 i 是需要步长为 k 的跳跃
// 而从位置 j 发起的跳跃最多不超过 j + 1
// 因为每次跳跃,下标至少增加 1,而步长最多增加 1
if (k <= j + 1) {
f[i][k] = f[j][k - 1] || f[j][k] || f[j][k + 1];
}
}
}
for (int i = 1; i < n; i++) {
if (f[n - 1][i]) return true;
}
return false;
}
}参考来源 Ref.
[1] leetcode 宫水三叶 【宫水三叶】一题四解 : 降低确定「记忆化容器大小」的思维难度