蓝桥杯——二分专题

news2024/11/26 8:23:34

二分分为：实数二分，二分理论题

二分套路题：最小值最大化，最大值最小化

运用二分满足条件：有界，单调。

1.两个二分模板

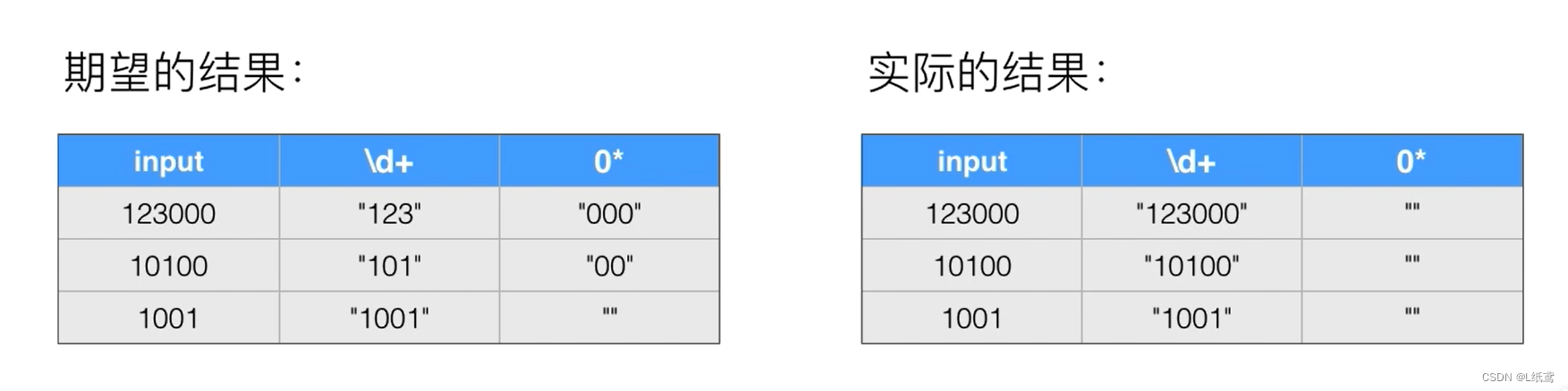
找>=x的第一个，mid=（low+high）//2 ，没有就找比他大的下一个数

a=[0,3,5,7,9,11,13]
# [0,1,2,3,4,5,6]
# low = 0 high =6 mid =3  ----->   low=4  high =6
# low = 4 high =6 mid =5  ----->   low=4  high =5
# low = 4 high =5 mid =4  ----->   low=5  high =5
# break   low=high=5
# 找的是靠右的那一个
low=0
high=len(a)-1
def search(low,high,x):  # 查找的是后一个
    while (low<high):
        mid =(low+high)//2   # (2+3)//2=2  偏左
        if (a[mid]>=x):
            high=mid
        else:
            low=mid+1
    print(a[low])
    print(a[high])
search(low,high,10)  # 查找结果10

找<=x的第一个，mid=（low+high+1）//2 ，没有就找比他小的前一个数

a=[0,3,5,7,9,11,13]
# [0,1,2,3,4,5,6]
# low = 0 high =6 mid =3  ----->   low=3  high =6
# low = 3 high =6 mid =5  ----->   low=3  high =4
# low = 3 high =4 mid =4  ----->   low=4  high =4
# break   low=high=4
# 找的是靠左的那一个
low=0
high=len(a)-1
def search(low,high,x):  # 查找的是前一个
    while (low<high):
        mid =(low+high+1)//2   # (2+3+1)//2=3  偏右
        if (a[mid]<=x):
            low=mid
        else:
            high=mid-1
    print(a[low])
    print(a[high])
search(low,high,10)  # 查找结果10

二分例题

1.分巧克力（根据题意转为二分，二分找边长N）

2.跳石头（根据题意转为二分，二分找d）

开始你在i(i=0)位置，我在跳下一步的时候去判断我这个当前跳跃的距离，如果这个跳跃距离比二分出来的mid小，那这就是一个不合法的石头，应该移走。为什么？我们二分的是最短跳跃距离，已经是最短了，如果跳跃距离比最短更短岂不是显然不合法，是这样的吧。移走之后要怎么做？先把计数器加上1，再考虑向前跳啊。去看移走之后的下一块石头，再次判断跳过去的距离，如果这次的跳跃距离比最短的长，那么这样跳是完全可以的，我们就跳过去，继续判断，如果跳过去的距离不合法就再拿走，这样不断进行这个操作，直到i = n+1，为啥是n+1？河中间有n块石头，显然终点在n+1处。（这里千万要注意不要把n认为是终点，实际上从n还要跳一步才能到终点）。