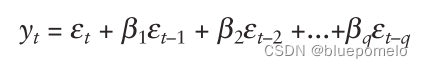本文是Quantitative Methods and Analysis: Pairs Trading此书的读书笔记。
这次我们构造一个由无限的白噪声实现(white noise realization) 组成的时间序列,即。这个由无限数目的项组成的值却是一个有限的值,比如
时刻的值为,
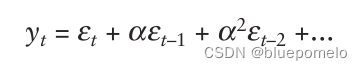
而时刻的值为:
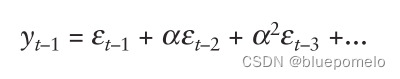
所以,把代入
,可以得到如下的式子,这个式子称为AR(1),即一阶自回归过程。
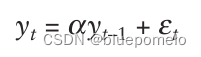
下图分别是自回归过程,以及它对应的自相关函数图。

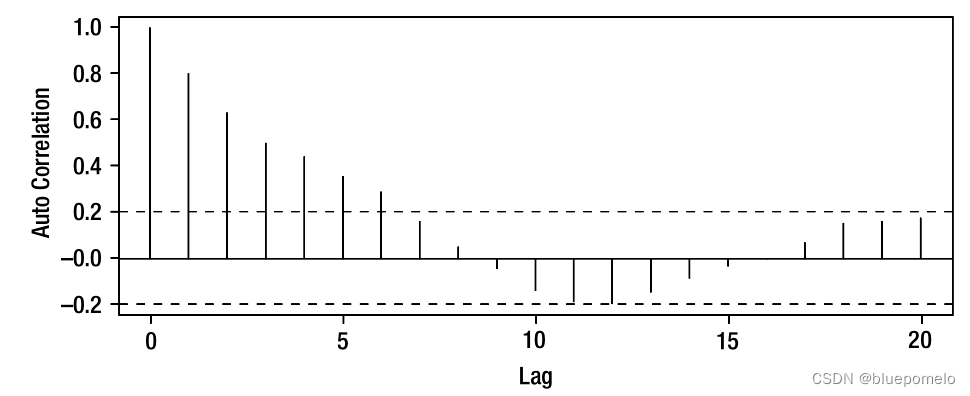
从自相关函数图可以看出,相关性随着时间间隔(lag)的增大逐渐减小,而不是突然减小。这是因为每个时间步骤中都有包括所有先前的白噪声实现。因此,无论时间序列的两个值相距多远,总会有共同的白噪声实现。所以相关性的减小这种变化是缓和的 。
自回归过程的可预测性:历史数据有助于预测下一刻的时序值。这种时间序列的预测值是一个来自条件均值为的正态分布的值,预测值的条件方差为
的方差,即构成该时间序列的白噪声的方差。
p阶段自回归过程AR(p)表示为:
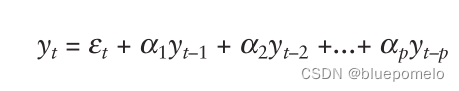
总结,自回归过程时间序列也是历史白噪声实现的线性组合。