本文是Quantitative Methods and Analysis: Pairs Trading此书的读书笔记。
我们从白噪声生成另一种时间序列。如下式:

这种时间序列的值由此刻的白噪声实现(white noise realization)加上beta倍的前一刻的白噪声实现。注意这个beta跟CAPM模型的beta没有任何关系,就是一个希腊字母而已。当beta=0时,这个时间序列就是一个白噪声序列。
这种时间序列称为Moving Average(MA) Process移动平均过程。下图分别是这种时间序列的图,以及它的自相关函数图。这里用到的序列是。
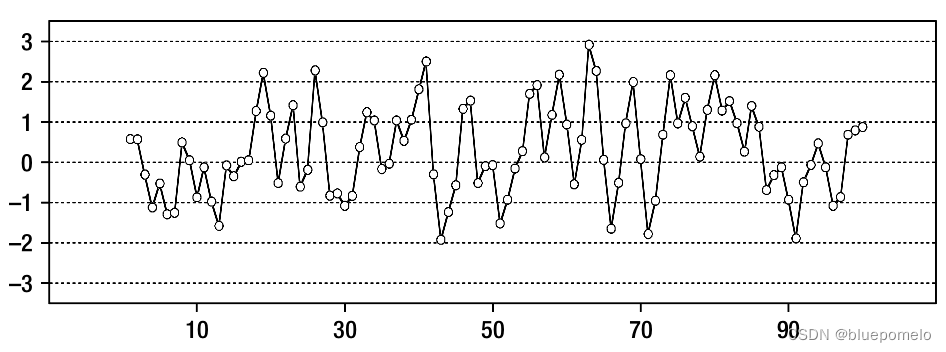
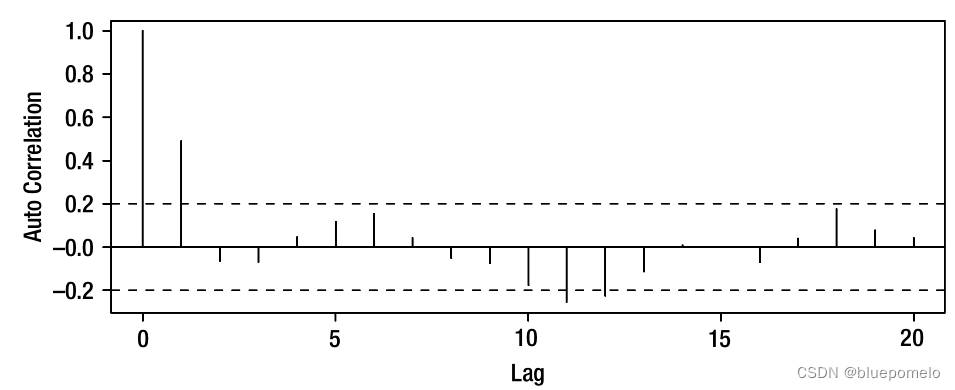
从自相关图可以看出,自相关性在lag=1之后就变得很小,为什么呢?我们来看看连续三个时刻的时间序列的值:
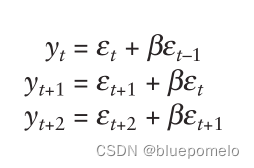
从上面的式子可以看出,时刻跟时刻
有共同的项
,
时刻和时刻
之间也有共同项
,所以,相差一个时间间隔(
)时有一定的相关性。但是时刻
和时刻
之间就没有共同的项,相差了两个时间间隔(
)时没有了相关性。白噪声的项都是从正态分布中独立地抽样出来的值,它们本来就是不相关的。因而之后随着时间间隔的加大,时序值之间都是不相关的。
移动平均过程的可预测性:历史数据是否有助于预测时间序列下一刻的值?答案是yes!
在时刻,我们知道前一刻
的白噪声实现,因此对时刻
的预测值是一个来自均值为
的正态分布的值。时刻
的预测值的方差就是
的方差,即构造移动平均过程时间序列的白噪声的方差。因为这些均值,方差都是来自历史数据的,所以称为时间序列的条件均值(conditional mean)、条件方差(conditional variance)。
总结,移动平均过程序列就是白噪声实现的线性组合。MA(1)表示使用的是此刻与前一刻的白噪声,称为first-order moving average process(一阶移动平均过程)。扩展到阶,即MA(q)如下式子:
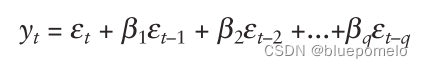








![[附源码]计算机毕业设计springboot个人博客系统](https://img-blog.csdnimg.cn/61bb191cf9bf43e3bdf18feb2ceee39c.png)