2021年全国研究生数学建模竞赛华为杯
C题 帕金森病的脑深部电刺激治疗建模研究
原题再现:
一、背景介绍
帕金森病是一种常见的神经退行性疾病,临床表现的特征是静止性震颤,肌强直,运动迟缓,姿势步态障碍等运动症状。目前缓解帕金森病症状的治疗方法主要有:药物治疗、手术治疗和脑深部刺激 (DBS) 三种。药物治疗用于早期帕金森疾病,手术治疗适用性较差且切除后不可逆。DBS通过精确定位,选取脑内特定的靶点植入刺激电极,通过输入高频电刺激,改变相应核团的兴奋性,达到改善治疗帕金森病症状的效果。DBS治疗帕金森病的靶点包括丘脑底核(STN)和苍白球内侧核(GPi/SNc)的脑深部电刺激等。
二、脑深部电刺激治疗
脑深部电刺激治疗帕金森病的机理来自基底神经节(Basal ganglia,BG),BG结构和丘脑-皮层(Thalamus-Cortex)结构如图1。与基底神经节相关的神经核团(Cortex,Striatum/dMSN/iMSN,SNc,GPe,GPi/SNc,STN,Thalamus)内部包括大量的神经元,核团之间相互连接,发生神经信息传递,经典的基底神经节神经团块结构中,神经信息的传导包括两条相互平行的信号传递通路[5]:直接通路(Cortex→Str→GPi/SNr)和间接通路(Cortex→Str→GPe→STN→GPi/SNr)。
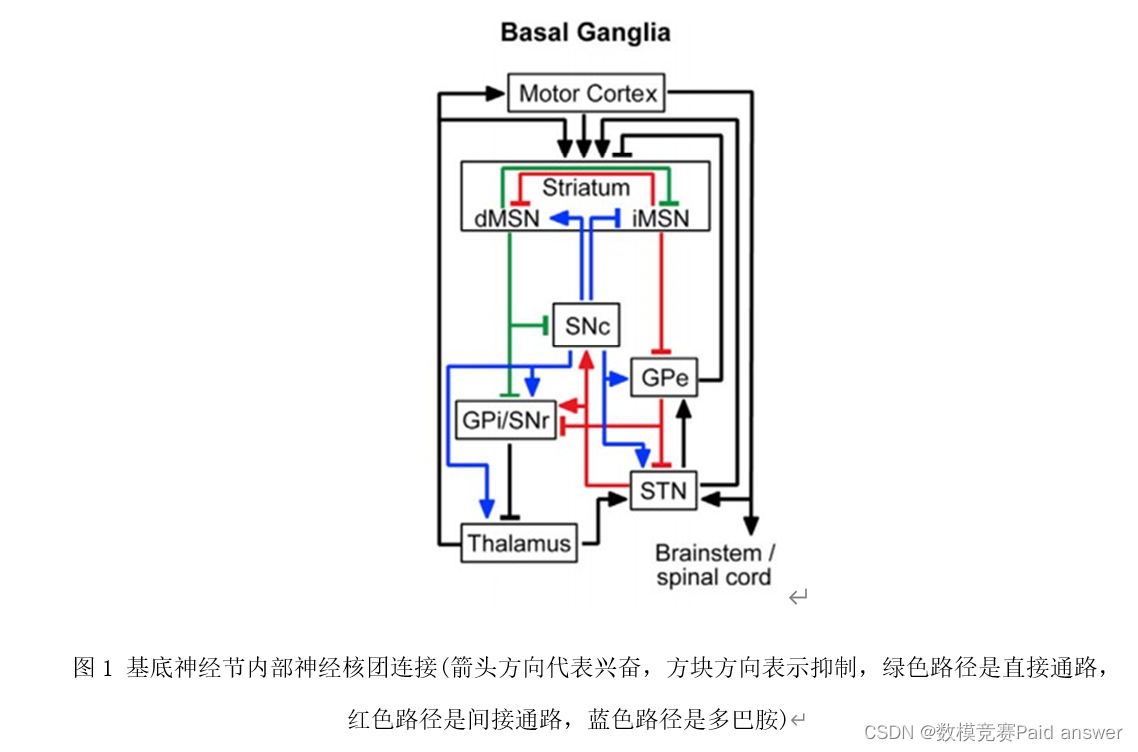
直接通路和间接通路分别通过丘脑兴奋或抑制运动皮层(图2)。虽然帕金森病的病理机制目前仍不十分清楚,但临床主流的观点是[6] :基底神经节黑质核团(SNc)多巴胺能神经元的退化,纹状体多巴胺减少,破坏直接通路和间接通路之间信息传递的平衡,导致运动控制紊乱,临床伴随帕金森症状。
STN直接参与基底神经节中直接通路的运动发起与间接通路的运动抑制之间的平衡。STN-DBS对改善PD运动障碍神经机制,优化DBS参数对PD治疗策略等具有重要意义。同样,GPi-DBS对PD运动控制也产生直接影响。
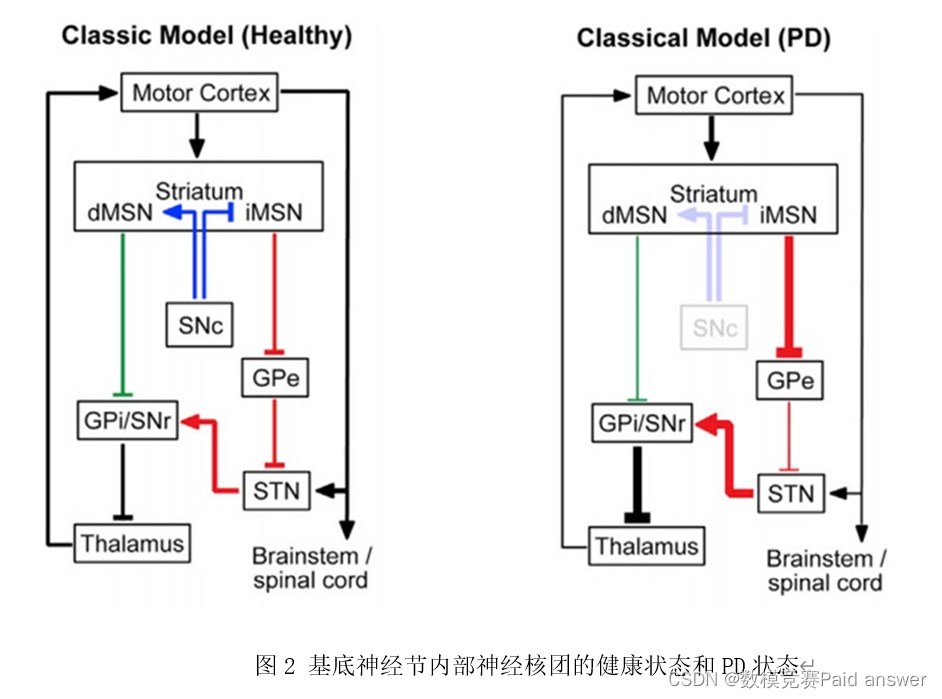
显然,帕金森病的脑深部刺激治疗的运动控制机理十分复杂,研究脑深部电刺激治疗的最优靶点选择和DBS参数(刺激强度和刺激频率等)优化,可以从基底神经节黑质核团的损害入手,模型分析基底神经节中神经元电位发放的特征指标;或者研究基底神经节中直接通路与间接通路之间的信息传递平衡,也许是解决PD难题的突破口。
三、请你建模回答如下问题:
问题1. 利用给出的神经元Hodgkin-Huxley模型(附件1),数值模拟外界刺激(包括直流刺激和交流刺激)情况下,单个神经元的电位发放情况,并给出神经元电位发放的特征指标。
问题2. 根据问题1的神经元Hodgkin-Huxley模型,结合附件1中神经元之间的突触连接理论,建立基底神经节神经回路的理论模型,计算基底神经节内部神经元的电位发放(每个神经团块可以简化为5-10个神经元)。
问题3. 根据建立的基底神经节回路模型,理论分析正常状态(图2中Healthy回路)和帕金森病态(图2 的PD回路中去掉黑质SNc)基底神经节回路电位发放的特征指标。
问题4. 利用建立的基底神经节回路模型,对帕金森病态的基底神经节靶点添加高频电刺激,可以模拟脑深部电刺激治疗帕金森病的状态。请模型确定最佳刺激靶点,是刺激靶点STN,还是刺激靶点GPi;请模型优化刺激的参数,如电刺激强度,电刺激频率和电刺激模式等。
问题5. 在直接通路的神经通路中,或者间接通路的神经通路中,模型回答脑深部电刺激治疗是否存在其它最优电刺激靶点。
整体求解过程概述(摘要)
帕金森病是一种常见的神经退行性疾病,本文针对 Hodgkin-Huxley(H-H)神经元模拟缓解帕金森病症状的脑深部刺激(DBS)治疗方法。基于 H-H 神经元模型建立基底神经节回路理论模型、健康状态模型、帕金森病态模型以及直接回路模型、间接回路模型,分析各个模型的电位发放情况并计算特征指标,确定模型的最佳刺激靶点并优化刺激参数。通过一系列数学建模与理论分析,研究 DBS 对帕金森病态治疗的意义。
针对问题 1,本文基于 H-H 神经元模型,考虑 H-H 神经元模型在直流刺激与交流刺激情况下,分别建立强迫 H-H 模型与非强迫 H-H 模型。通过改变外界刺激的参数,主要是刺激振幅 A 与刺激频率 F,来判断对单个 H-H 神经元的电位发放特征指标的影响。采用四阶龙格-库塔(RK4)算法将上述模型进行离散化处理,设置初始条件与约束条件,得到离散化模型。运用 MATLAB 软件编程,数值模拟单个神经元丰富的放电行为,最后给出了几组单个神经元放电行为的时域图并计算特征指标,如表 1 和表 2 所示。在交流刺激下,单个神经元放电状态有峰发放行为与簇发放行为;在直流刺激下,单个神经元放电状态只有峰发放行为。
针对问题 2,本文利用问题 1 的 H-H 神经元模型,建立基底神经节神经回路模型。将一个神经核团内部神经元数量简化为 8 条,8 条神经元之间通过电突触单向连接,构成一个环形神经核团。同时该基底神经节神经回路模型需要 8 个神经核团,核团与核团之间通过兴奋和抑制两种化学突触连接,从而建立一个庞大的基底神经节神经回路,采用问题 1 同样的 RK4 算法进行求解。最终,得到一组神经回路模型中的 Cor、GPE、GPi、STN 神经核团的放电时域图如图 5.6 所示。对于这 4 个神经核团而言,正常状态下都能够对来自外界的交流刺激进行正确的尖峰响应,且其幅值稳定在 50mV 左右。对于 STN 神经元来说,在外界交流刺激情况下其放电频率较小、放电状态较稀疏,具有一定规律性。而GPe 和 GPi 的放电频率相对较高,Cor 的放电频率相对较低。
对于问题 3,本文建立正常状态和帕金森病态(PD)的基底神经节回路模型,其连接方式与问题二中的神经元内部与神经核团内部之间耦合方式相同。首先,建立正常状态的神经网络,然后在其基础上去掉 SNc 核团构建 PD 神经网络。对这两个模型进行算法求解并计算电位发放的特征指标。通过仿真得到的时域图如图 5.9 所示,观察出在健康状态下的放电行为是平稳的;在 PD 状态下的放电行为是紊乱的。
对于问题 4,本文在问题 3 中的 PD 基底神经节模型上,对刺激靶点 STN 和 GPi 添加高频电刺激,来模拟脑深部电刺激治疗帕金森兵的状态。对于子问题 1,采用最小二乘法建立一个判断标准,它通过最小化误差的平方和寻找数据的最佳函数匹配。针对 STN 靶点和 GPi 靶点,刻画出 STN、GPe、THa、GPi 四个神经元核团中第一个神经元的电位发放情况如图 5.11 所示,计算通过交流刺激与方波刺激这两种靶点时该神经元的特征指标如表 4 与表 5 所示。通过刺激神经节靶点 STN 的品质因数远小于刺激靶点 GPi 的品质因数比较,最终得出结论:最佳刺激靶点为 STN 靶点,最优刺激模式为交流刺激模式。对于子问题 2,运用分层思想求解多目标的方法,来达到优化电刺激强度、电刺激频率以及电刺激模式参数的目的。
对于问题 5,本文考虑在直接通路或间接通路中,DBS 是否存在其他最优电刺激靶点。根据要求建立直接通路的神经网络模型,采用同问题 4 一样的最小二乘方法得到模型的最佳函数匹配。针对建立的直接神经通路模型,选取直接通路的 4 个神经核团中的一个神经元进行研究,对符合最优刺激靶点范围的 4 个靶点施加外界刺激后的电位发放情况指标如表 7 所示,并绘制柱状图如图 5.14 所示。由图表可以看出靶点 dMSN 在外界交流刺激情况下放电频率较大,品质因数 Q 较小,且与正常情况下的品质因数较为贴近。因此,最终得出结论,脑深部电刺激治疗存在其他最优电刺激靶点。
模型假设:
假设 1:每一个神经核团内部都有 8 条神经元。
假设 2:每一个神经和核团内部的 8 条神经元都是单向电突触耦合连接,构成一个环形连接。
假设 3:神经元模型的初始状态均为零。
假设 4:单个神经元之间的电突触与化学突触的耦合权重保持不变。
假设 5:Cortex 为第 1 个核团,dMSN 为第 2 个核团,iMSN 为第 3 个核团,SNc 为第 4 个核团,GPe 为第 5 个核团,GPi/SNc 为第 6 个团,Thalamus 为第 7 个核团,STN 为第 8 个核团。
问题分析:
本文对帕金森病的脑深部电刺激 (DBS) 治疗进行建模研究,DBS 通过精确定位,选取脑内特定的靶点植入刺激电极,通过输入高频电刺激,改变相应核团的兴奋性,达到改善治疗帕金森病症状的效果。本文根据不同的条件约束不同的目标,具体问题分析如下:
针对问题一:问题一在给出的神经元 H-H 模型的基础上,考虑在外界的直流刺激和交流刺激两种情况下,建立两个新的神经元模型,一个是直流刺激情况下的强迫神经元模型,一个是交流刺激情况下的非强迫神经元模型。对于所建立的神经元模型,采用四阶龙格-库塔 (RK4) 算法将其进行离散化处理,得到离散化模型,设置约束条件。运用 MATLAB软件编程,数值模拟单个神经元丰富的放电行为,观察几组单个神经元电位发放情况的时域波形,并计算其特征指标,从而解决问题一。
针对问题二:问题二利用问题 1 的 H-H 神经元模型,建立基底神经节神经回路模型,每个神经核团内部神经元数量为 8 条,8 条神经元进行单向连接,构成一个环形小网络,核团与核团之间根据基底神经节内部神经核团连接图进行兴奋和抑制突触耦合建立一个庞大的神经网络。同样采用 RK4 算法,运用 MATLAB 软件编程,数值模拟神经网络丰富的放电行为,给出几组单个神经元电位发放情况的时域波形图,并计算其特征指标,从而解决问题二。
针对问题三:问题三在问题二建立的基底神经节回路模型基础上,建立正常状态和帕金森病态 (PD) 的基底神经节回路模型,其连接方式与问题二中的神经元内部与神经核团内部之间耦合方式相同。首先,建立正常状态的神经网络,然后在其基础上去掉 SNc 核团构建 PD 神经网络。对这两个模型进行算法求解并计算电位发放的特征指标。通过仿真得到放电情况的时域图,观察在健康状态与 PD 状态下的放电行为是平稳的还是紊乱的。
针对问题四:问题四在问题三的 PD 基底神经节模型基础上,对刺激靶点 STN 和 GPi添加高频电刺激,来模拟脑深部电刺激治疗帕金森病的状态。对于子问题 1,采用最小二乘法建立一个判断标准,它通过最小化误差的平方和寻找数据的最佳函数匹配,求解最佳刺激靶点与最优刺激模式。对于子问题 2,运用分层思想求解多目标的方法,来达到优化电刺激强度、电刺激频率以及电刺激模式参数的目的。
针对问题五:问题五考虑在直接通路或间接通路中,DBS 是否存在其他最优电刺激靶点。根据要求建立直接通路的神经网络模型,采用同问题四一样的最小二乘方法得到模型的最佳函数匹配。最终,分析探讨脑深部电刺激治疗是否存在其他最优电刺激靶点。
模型的建立与求解
问题一在给出的神经元 Hodgkin-Huxley 模型的基础上,考虑在外界的直流刺激和交流刺激两种情况下,建立两个新的神经元模型,一个是直流刺激情况下的强迫神经元模型,一个是交流刺激情况下的非强迫神经元模型。对于所建立的神经元模型,采用四阶龙格-库塔 (RK4) 算法将其进行离散化处理,得到离散化模型。运用 MATLAB 软件编程,数值模拟单个神经元的位发放情况,并计算其特征指标。
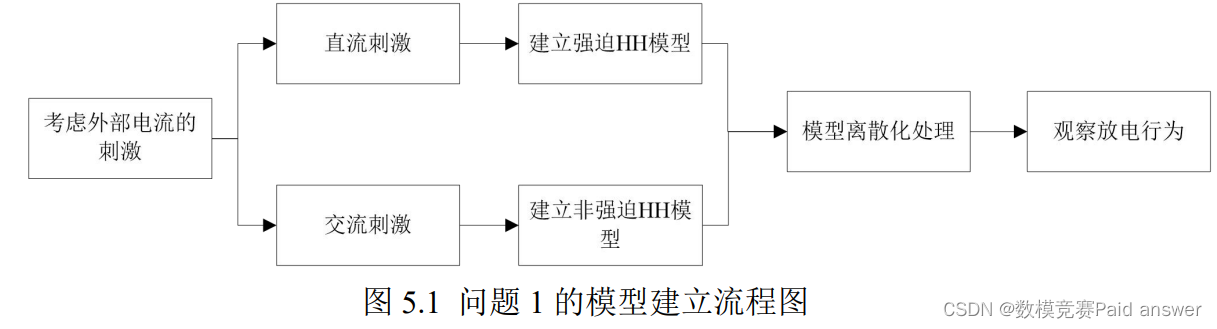
A H-H 模型的建立
在静息状态下,神经元膜内外的离子浓度不同形成神经细胞的膜电位。当神经系统受到外界刺激时,膜电位产生的动作电位可以形成电位发放,这些动作电位的峰发放和簇发放形成神经系统的信息传递编码,典型的神经元膜电位可由给出的 H-H 神经元模型描述. 由于本题只考虑外界对神经元的刺激影响,因此在不考虑突触 Isynapse 的情况下,即Isynapse = 0。基于神经元 H-H 模型外加直流刺激与交流刺激,就可以建立强迫 H-H 神经元模型与非强迫 H-H 神经元模型如下所示:

当 Iexternal 为常数时,即 Iexternal = N ,模型(1)为强迫 H-H 模型;当 Iexternal = Asin(2πFt)时,模型(1)为非强迫 H-H 模型

a 求解原理


b 多步骤求解

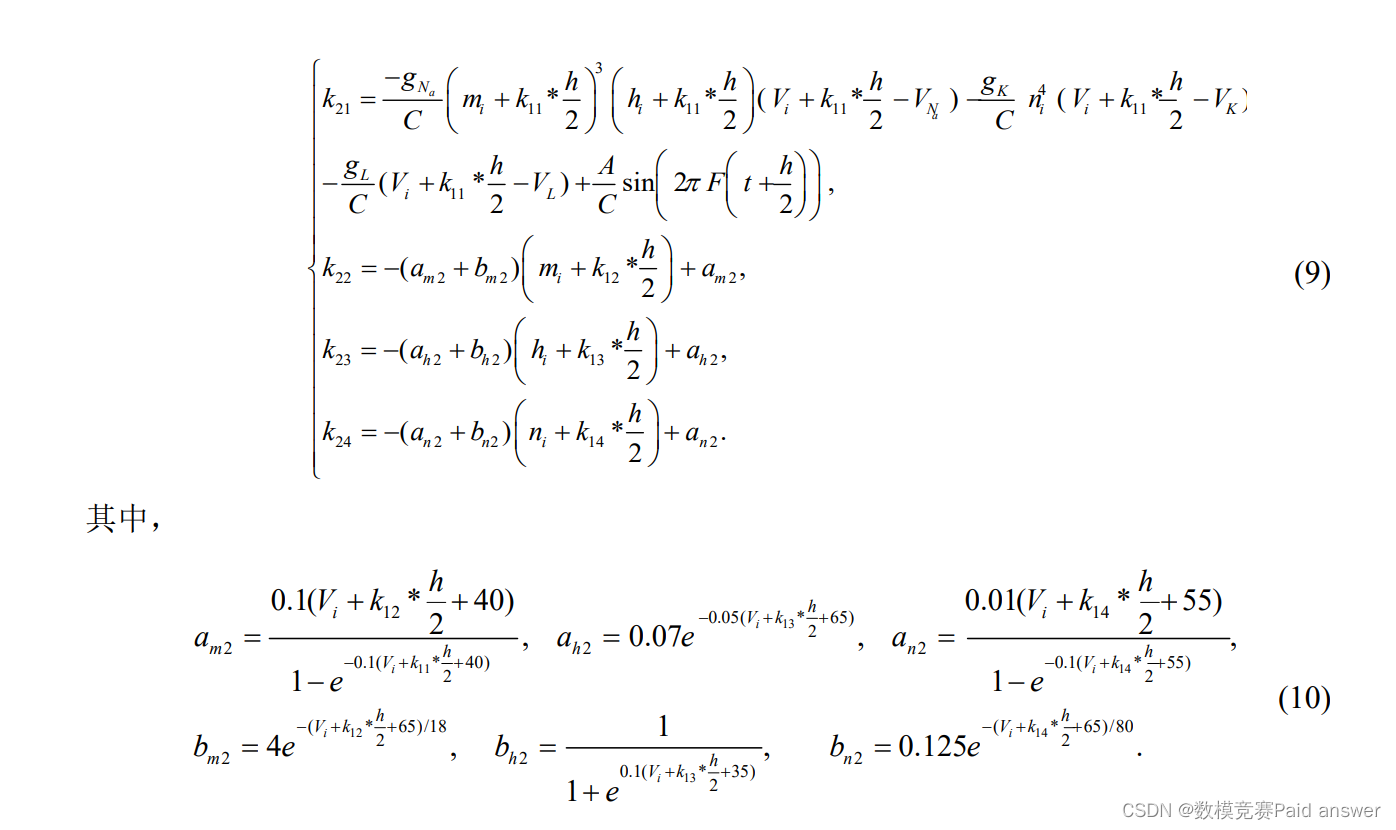


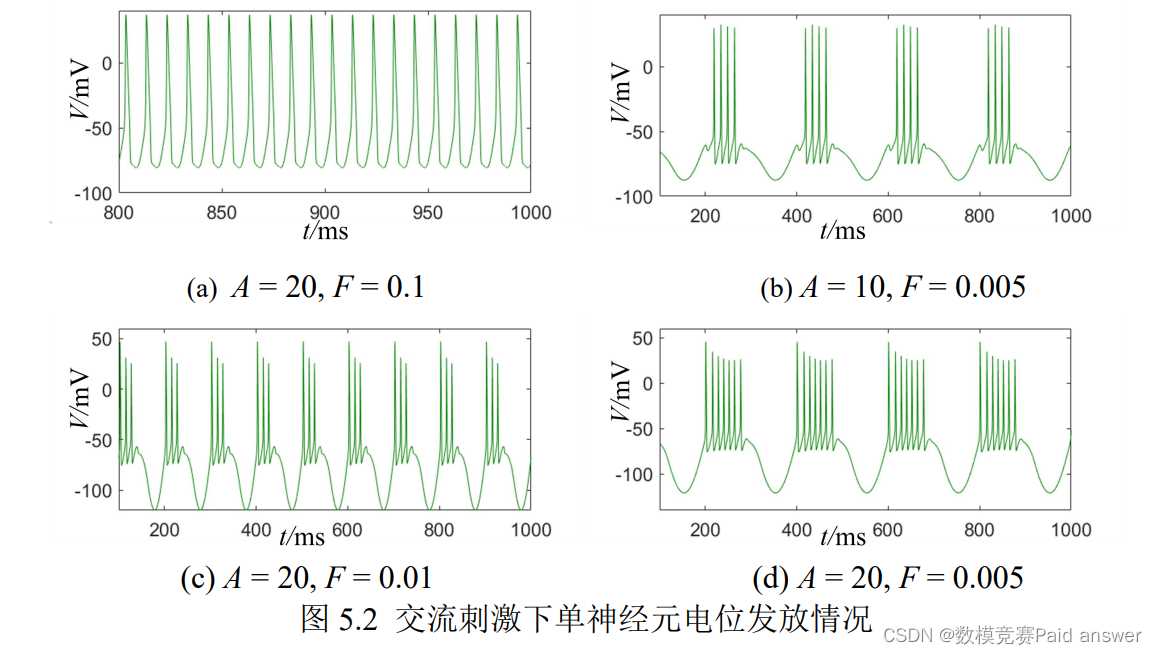
对于所建立的强迫 H-H 神经元模型与非强迫 H-H 神经元模型,采用 RK4 算法将其进行离散化处理,得到离散化模型。分别将直流刺激的振幅 A 与交流刺激的振幅 A、频率 F 作为可调节参数,设置仿真步长 0.01,时长为 1000,初始条件为 V(0) = m(0) = h(0) = n(0) = 0,观察在不同区间内的神经元的丰富的放电行为,数值模拟几组单个神经元电位发放情况,选取了四组参数 A、F,进行 MATLAB 数值仿真与理论分析,得到交流刺激下非强迫 H-H 神经元模型放电行为的时域图,如图 5.2 所示。
可以看出,当参数 A = 20, F = 0.1 时,非强迫 H-H 神经元模型的电位发放行为是峰发放行为;当参数 A = 10, F = 0.005、 A = 20, F = 0.01、A = 20, F = 0.005 时,非强迫 H-H 神经元模型的电位发放行为都是簇发放行为。因此,建立的非强迫 H-H 神经元模型与强迫 H-H 神经元模型都具有丰富的放电行为。
针对直流刺激下神经元电位发放情况,选取了两组参数 A,分别为 A = 10、A = 30,进行 MATLAB 数值仿真与理论分析,得到直流刺激下非强迫 H-H 神经元模型放电行为的时域图。可以看出,在不同振幅 A 下,强迫 H-H 神经元模型的电位发放行为都是峰发放。有区别的是,峰发放行为的频率根据施加直流激励振幅的大小不同而有所不同。
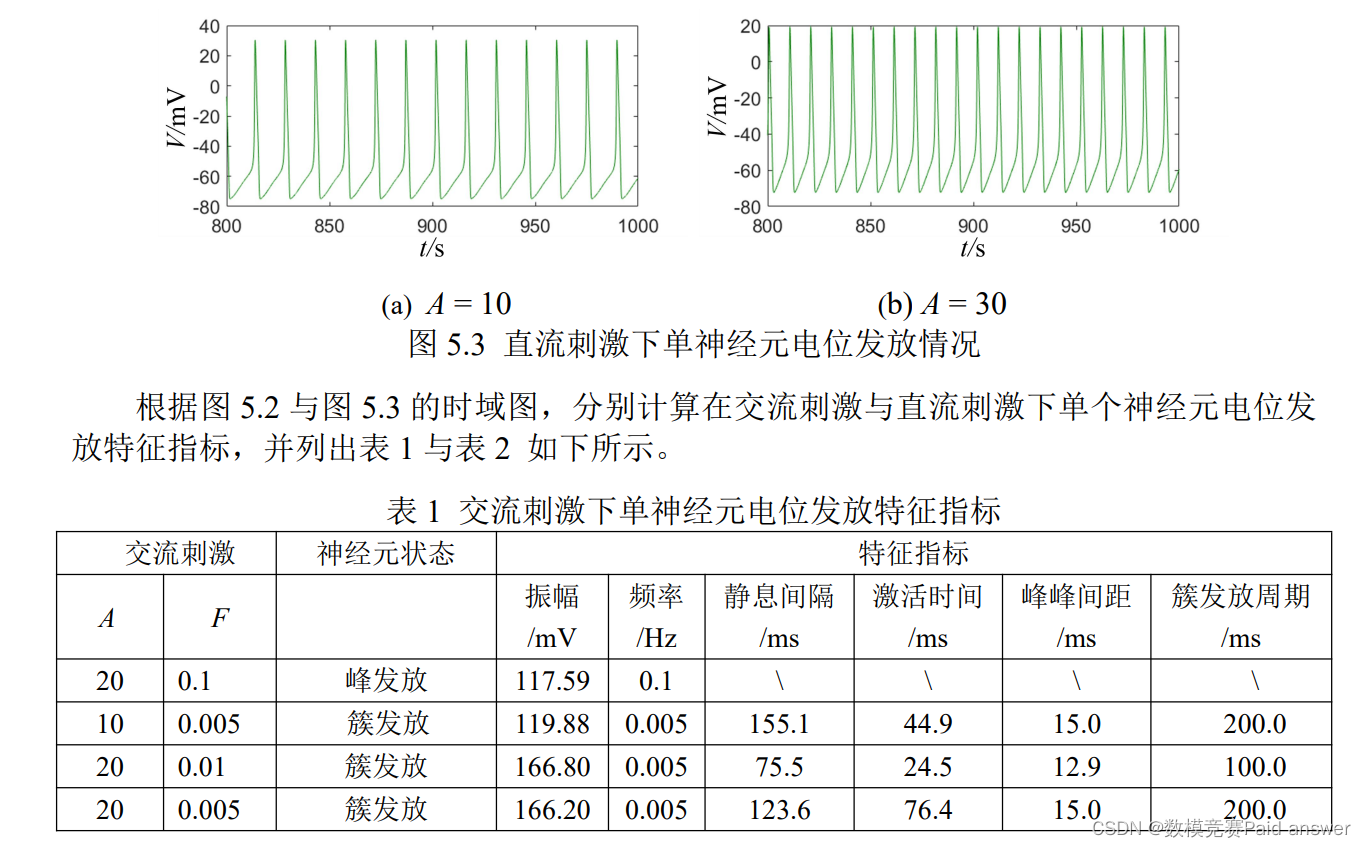

由表 1 可以看出,在交流刺激下,当振幅 A 相同时,频率 F 越小,非强迫 H-H 神经元模型的簇发放行为的激活时间、峰峰间距、静息间隔越长,簇发放周期也越长。当频率F 增大到一定值时,非强迫 H-H 神经元模型的电位发放行为会变为簇发放行为。当频率 F相同时,振幅 A 越小,非强迫 H-H 神经元模型的簇发放行为的激活时间越短,静息间隔越长,簇发放周期相同,振幅越大。根据占空比 = 激活时间/簇发放周期,当 A = 10,F = 0.005时,簇发放的占空比为 22.45%;当 A = 20,F = 0.01 时,簇发放的占空比为 75.5%;当 A =20,F = 0.005,簇发放的占空比为 61.8%。由表 2 可以看出,在直流刺激下,强迫 H-H 神经元模型的电位发放行为都是峰发放行为。当振幅 A 越大时,峰发放行为的振幅越小,平均频率越大。
问题二要求根据问题一的神经元 H-H 模型,建立基底神经节神经回路的理论模型。根据基底神经节内部神经核连接图,首先需要将 5 到 10 个神经元连接而成一个神经核团,而每个神经元之间的连接方式可以通过单向连接、双向连接等其他电突触耦合连接方式进行连接。这里我们通过单向环形连接方式连接 8 个神经元构成 1 个神经核团,同时该基底神经节神经回路需要 8 个神经核团,然后将神经核团与神经核团之间通过化学突触连接,从而构成基底神经节神经回路的模型。最后根据建立的基底神经节神经回路理论模型利用RK 算法进行 MATLAB 软件编程,观察神经回路模型的时域波形图,分析其电位发放情况。
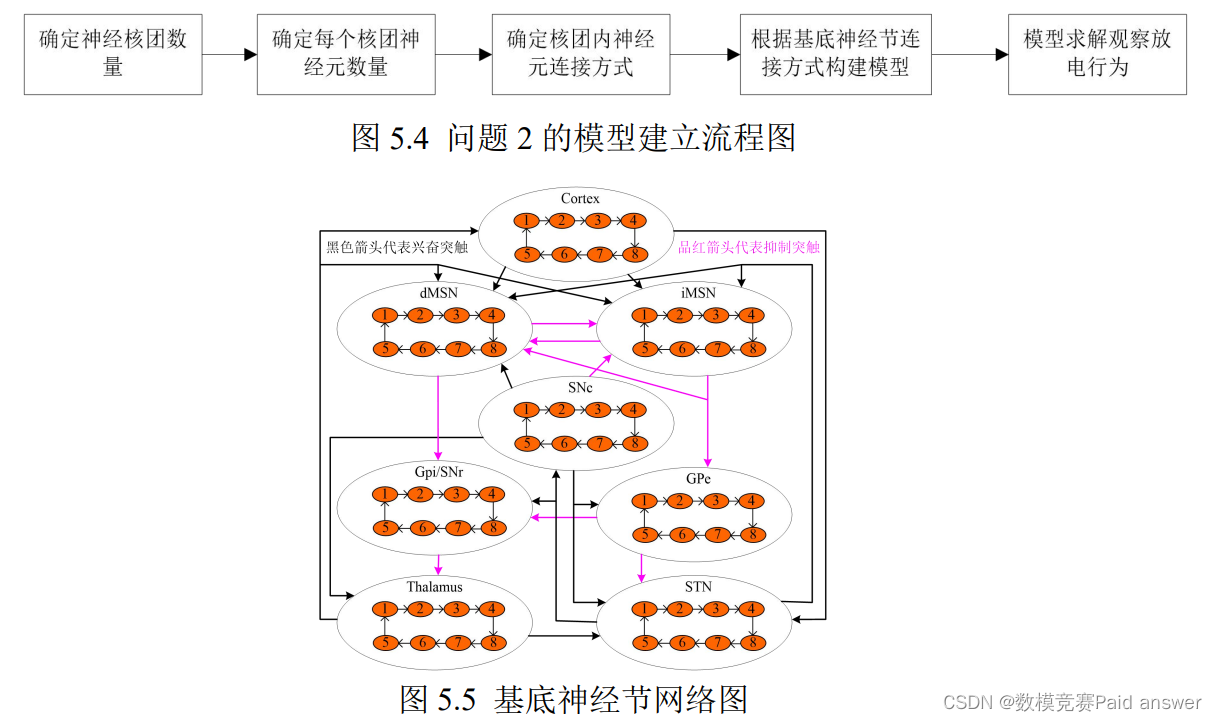
问题二设定每个神经核团中的内部神经元连接方式为单向环形连接,根据基底神经节内部神经核团连接图(箭头方向代表兴奋,方块方向表示抑制,绿色路径是直接通路,红色路径是间接通路,蓝色路径是多巴胺),绘制基底神经节网络图如图 5.5 所示。
A 神经核团模型的建立
神经元之间的突触连接有化学突触和电突触两类,电突触比较简单,就是直接的耦合连接,化学突触主要有兴奋突触和抑制突触,考虑到基底神经节涉及到一个庞大的网络系统。首先,本文通过电突触耦合方式单向连接 8 个神经元来建立一个环形的神经核团模型,其次通过基底神经节内部神经核团连接图采用化学突触耦合方式将 8 个神经核团连接起来,最终构建一个庞大的网络基础,就是要求建立的基底神经节神经回路模型。基于上述思想,将 8 个神经元电耦合连接成的 1 个神经核团的模型描述如下
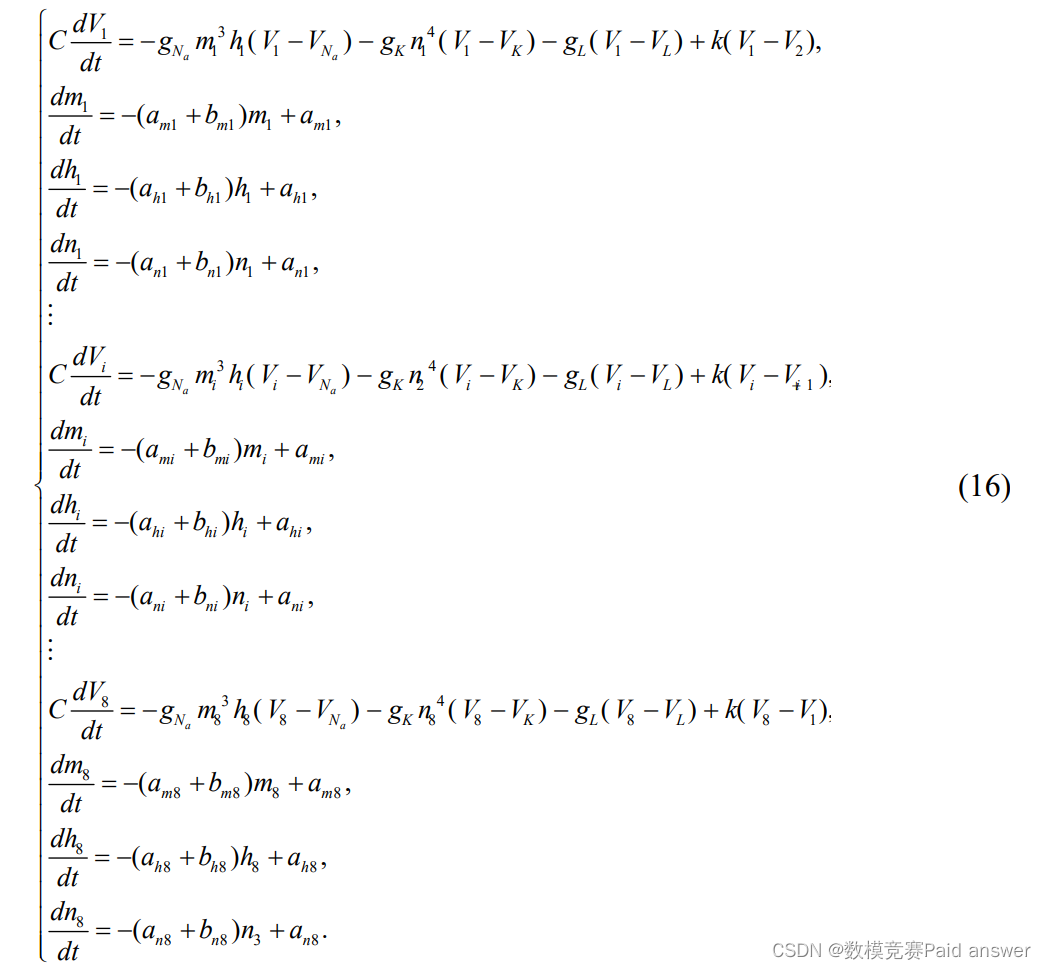
其中,i = 1, 2 , 3 ,…, 8,代表了 1 个神经核团内部的 8 个 H-H 神经元。
B 确定初始条件与约束条件



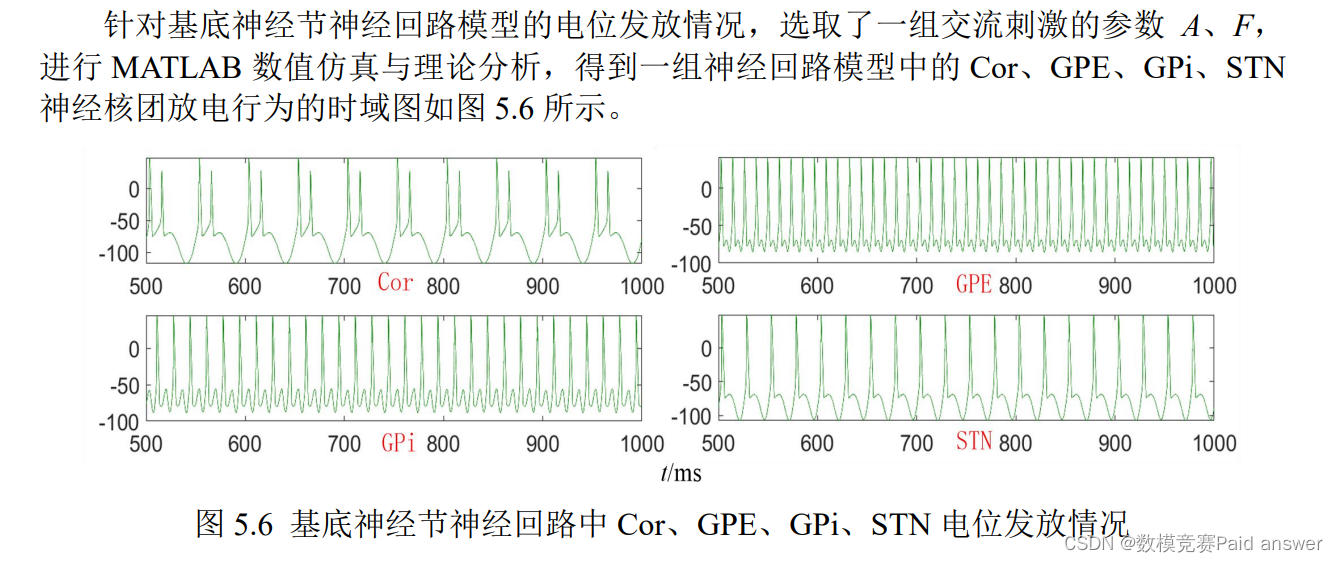
从图 5.6 中可以看到,对于神经回路模型中的 Cor、GPE、GPi、STN 神经核团而言,正常状态下都能够对每一个来自外界的交流刺激进行正确的尖峰响应,且其幅值稳定在50mV 左右。对于 STN 神经元来说,在外界交流刺激情况下其放电频率较小,且它的放电状态较为稀疏,但具有一定的规律性。而 GPe 和 GPi 的放电频率相对较高,Cor 的放电频率相对较低。
A 正常状态和 PD 状态神经回路模型的建立
问题三是问题二的延伸,即在问题二的基础上建立一个基底内部健康神经网络与 PD状态神经网络。首先,建立正常状态的神经网络,然后在健康神经网络的基础上去掉核团4,即 SNc 核团,这样便构建了 PD 状态神经网络。
B 确定初始条件与约束条件
a 初始条件



选取一组参数,当振幅 A = 150,频率 F = 1 时,通过模型求解研究基底神经节神经元回路的电位发放情况,这里只给出了神经回路内部的某个神经元在正常状态下和 PD 病态下的时域图,如图 5.9 所示
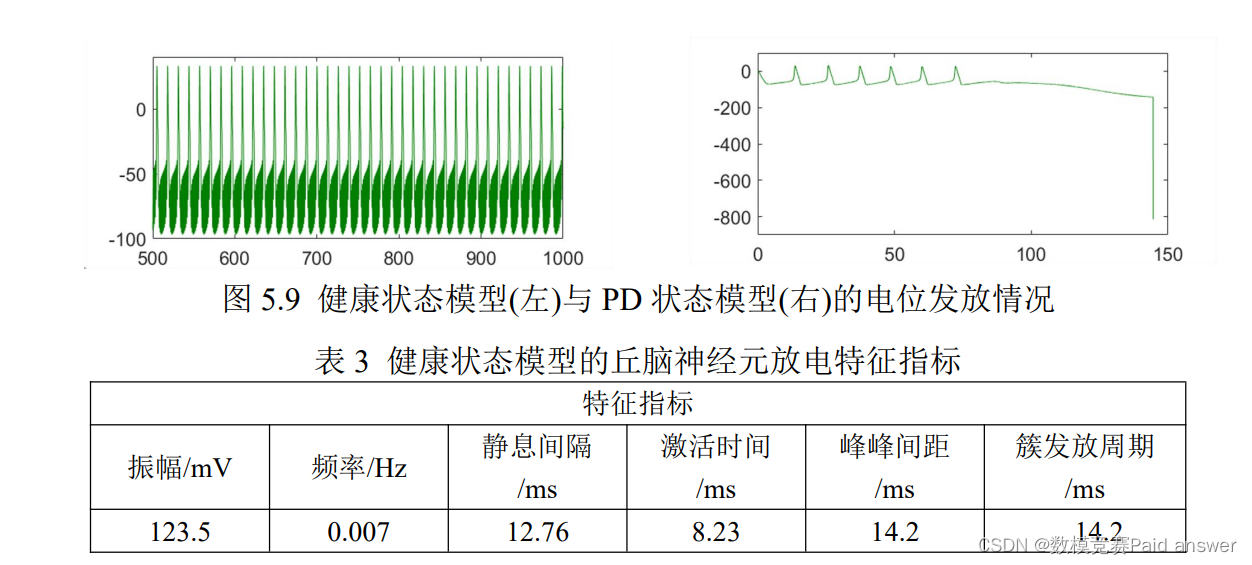
可以看出,正常状态下的丘脑神经元模型的电位发放情况是正常的峰发放行为,PD状态下的丘脑神经元模型的放电状态逐渐开始紊乱,说明各个神经元或神经核团之间的信息传递平衡已经被破坏了,证明了帕金森病态的出现。从而无法观测出神经元的性能指标。
论文缩略图:



全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
问题一程序
format long
tspan=0:1e-2:1000;
Y0=[0 0 0 0];
[t,y]=ode45Ps(@H-H,tspan,Y0);
figure(1)
plot(t(t>200,1),y(t>200,1));
hold on 次程序
function dy=H-H(t,y)
dy=zeros(4,1);
g1=120;g2=36;g3=0.3;
V1=50;V2=-77;V3=-54.5; a1=0.1*(y(1)+40)/(1-exp(-0.1*(y(1)+40)));
b1=4*exp(-(y(1)+65)/18); a2=0.07*exp(-0.05*(y(1)+65));
b2=1/(1+exp(-0.1*(y(1)+35))); a3=0.01*(y(1)+55)/(1-exp(-0.1*(y(1)+55)));
b3=0.125*exp(-(y(1)+65)/80);
A=20;
F=0.1;
dy(1)= -g1*(y(2)^3)*y(3)*(y(1)-V1)-g2*(y(4)^4)*(y(1)-V2)-g3*(y(1)-V3)+A*sin(2*pi*F*t);
dy(2)= -(a1+b1)*y(2)+a1;
dy(3)= -(a2+b2)*y(3)+a2;
dy(4)= -(a3+b3)*y(4)+a3;
直流刺激
主程序
format long
tspan=0:1e-2:1000;
Y0=[0 0 0 0];
[t,y]=ode45Ps(@H-H,tspan,Y0);
figure(1)
plot(t(t>200,1),y(t>200,1));
hold on 次程序
function dy=H-H(t,y)
dy=zeros(4,1);
g1=120;g2=36;g3=0.3;
V1=50;V2=-77;V3=-54.5; a1=0.1*(y(1)+40)/(1-exp(-0.1*(y(1)+40)));
b1=4*exp(-(y(1)+65)/18); a2=0.07*exp(-0.05*(y(1)+65));
b2=1/(1+exp(-0.1*(y(1)+35))); a3=0.01*(y(1)+55)/(1-exp(-0.1*(y(1)+55)));
b3=0.125*exp(-(y(1)+65)/80);
A=10;
dy(1)= -g1*(y(2)^3)*y(3)*(y(1)-V1)-g2*(y(4)^4)*(y(1)-V2)-g3*(y(1)-V3)+A;
dy(2)= -(a1+b1)*y(2)+a1;
dy(3)= -(a2+b2)*y(3)+a2;
dy(4)= -(a3+b3)*y(4)+a3;
问题二程序
function dy=CNN(t,y)
dy=zeros(98,1);
g1=120;g2=36;g3=0.3;k=0.001;
V1=50;V2=-77;V3=-54.5;
A=10;
F=0.005; a1=0.1*(y(1)+40)/(1-exp(-0.1*(y(1)+40))); a2=0.07*exp(-0.05*(y(1)+65)); a3=0.01*(y(1)+55)/(1-exp(-0.1*(y(1)+55))); a4=0.1*(y(5)+40)/(1-exp(-0.1*(y(5)+40))); a5=0.07*exp(-0.05*(y(5)+65)); a6=0.01*(y(5)+55)/(1-exp(-0.1*(y(5)+55))); a7=0.1*(y(9)+40)/(1-exp(-0.1*(y(9)+40))); a8=0.07*exp(-0.05*(y(9)+65)); a9=0.01*(y(9)+55)/(1-exp(-0.1*(y(9)+55))); a10=0.1*(y(13)+40)/(1-exp(-0.1*(y(13)+40))); a11=0.07*exp(-0.05*(y(13)+65)); a12=0.01*(y(13)+55)/(1-exp(-0.1*(y(13)+55))); a13=0.1*(y(17)+40)/(1-exp(-0.1*(y(17)+40))); a14=0.07*exp(-0.05*(y(17)+65)); a15=0.01*(y(17)+55)/(1-exp(-0.1*(y(17)+55))); a16=0.1*(y(21)+40)/(1-exp(-0.1*(y(21)+40))); a17=0.07*exp(-0.05*(y(21)+65)); a18=0.01*(y(21)+55)/(1-exp(-0.1*(y(21)+55))); a19=0.1*(y(25)+40)/(1-exp(-0.1*(y(25)+40))); a20=0.07*exp(-0.05*(y(25)+65)); a21=0.01*(y(25)+55)/(1-exp(-0.1*(y(25)+55))); a22=0.1*(y(29)+40)/(1-exp(-0.1*(y(29)+40))); a23=0.07*exp(-0.05*(y(29)+65)); a24=0.01*(y(29)+55)/(1-exp(-0.1*(y(29)+55)));
a25=0.1*(y(33)+40)/(1-exp(-0.1*(y(33)+40))); a26=0.07*exp(-0.05*(y(33)+65)); a27=0.01*(y(33)+55)/(1-exp(-0.1*(y(33)+55))); a28=0.1*(y(37)+40)/(1-exp(-0.1*(y(37)+40))); a29=0.07*exp(-0.05*(y(37)+65)); a30=0.01*(y(37)+55)/(1-exp(-0.1*(y(37)+55))); a31=0.1*(y(41)+40)/(1-exp(-0.1*(y(41)+40))); a32=0.07*exp(-0.05*(y(41)+65)); a33=0.01*(y(41)+55)/(1-exp(-0.1*(y(41)+55))); a34=0.1*(y(45)+40)/(1-exp(-0.1*(y(45)+40))); a35=0.07*exp(-0.05*(y(45)+65)); a36=0.01*(y(45)+55)/(1-exp(-0.1*(y(45)+55))); a37=0.1*(y(49)+40)/(1-exp(-0.1*(y(49)+40))); a38=0.07*exp(-0.05*(y(49)+65)); a39=0.01*(y(49)+55)/(1-exp(-0.1*(y(49)+55))); a40=0.1*(y(53)+40)/(1-exp(-0.1*(y(53)+40))); a41=0.07*exp(-0.05*(y(53)+65)); a42=0.01*(y(53)+55)/(1-exp(-0.1*(y(53)+55))); a43=0.1*(y(57)+40)/(1-exp(-0.1*(y(57)+40))); a44=0.07*exp(-0.05*(y(57)+65)); a45=0.01*(y(57)+55)/(1-exp(-0.1*(y(57)+55))); a46=0.1*(y(61)+40)/(1-exp(-0.1*(y(61)+40))); a47=0.07*exp(-0.05*(y(61)+65)); a48=0.01*(y(61)+55)/(1-exp(-0.1*(y(61)+55))); a49=0.1*(y(65)+40)/(1-exp(-0.1*(y(65)+40))); a50=0.07*exp(-0.05*(y(65)+65)); a51=0.01*(y(65)+55)/(1-exp(-0.1*(y(65)+55))); a52=0.1*(y(69)+40)/(1-exp(-0.1*(y(69)+40))); a53=0.07*exp(-0.05*(y(69)+65)); a54=0.01*(y(69)+55)/(1-exp(-0.1*(y(69)+55))); a55=0.1*(y(73)+40)/(1-exp(-0.1*(y(73)+40))); a56=0.07*exp(-0.05*(y(73)+65)); a57=0.01*(y(73)+55)/(1-exp(-0.1*(y(73)+55))); a58=0.1*(y(77)+40)/(1-exp(-0.1*(y(77)+40))); a59=0.07*exp(-0.05*(y(77)+65)); a60=0.01*(y(77)+55)/(1-exp(-0.1*(y(77)+55))); a61=0.1*(y(81)+40)/(1-exp(-0.1*(y(81)+40))); a62=0.07*exp(-0.05*(y(81)+65)); a63=0.01*(y(81)+55)/(1-exp(-0.1*(y(81)+55))); a64=0.1*(y(85)+40)/(1-exp(-0.1*(y(85)+40))); a65=0.07*exp(-0.05*(y(85)+65)); a66=0.01*(y(85)+55)/(1-exp(-0.1*(y(85)+55))); a67=0.1*(y(89)+40)/(1-exp(-0.1*(y(89)+40))); a68=0.07*exp(-0.05*(y(89)+65));
a69=0.01*(y(89)+55)/(1-exp(-0.1*(y(89)+55))); a70=0.1*(y(93)+40)/(1-exp(-0.1*(y(93)+40))); a71=0.07*exp(-0.05*(y(93)+65)); a72=0.01*(y(93)+55)/(1-exp(-0.1*(y(93)+55)));
b1=4*exp(-(y(1)+65)/18);
b2=1/(1+exp(-0.1*(y(1)+35)));
b3=0.125*exp(-(y(1)+65)/80);
b4=4*exp(-(y(5)+65)/18);
b5=1/(1+exp(-0.1*(y(5)+35)));
b6=0.125*exp(-(y(5)+65)/80);
b7=4*exp(-(y(9)+65)/18);
b8=1/(1+exp(-0.1*(y(9)+35)));
b9=0.125*exp(-(y(9)+65)/80);
b10=4*exp(-(y(13)+65)/18);
b11=1/(1+exp(-0.1*(y(13)+35)));
b12=0.125*exp(-(y(13)+65)/80);
b13=4*exp(-(y(17)+65)/18);
b14=1/(1+exp(-0.1*(y(17)+35)));
b15=0.125*exp(-(y(17)+65)/80);
b16=4*exp(-(y(21)+65)/18);
b17=1/(1+exp(-0.1*(y(21)+35)));
b18=0.125*exp(-(y(21)+65)/80);
b19=4*exp(-(y(25)+65)/18);
b20=1/(1+exp(-0.1*(y(25)+35)));
b21=0.125*exp(-(y(25)+65)/80);
b22=4*exp(-(y(29)+65)/18);
b23=1/(1+exp(-0.1*(y(29)+35)));
b24=0.125*exp(-(y(29)+65)/80);
b25=4*exp(-(y(33)+65)/18);
b26=1/(1+exp(-0.1*(y(33)+35)));
b27=0.125*exp(-(y(33)+65)/80);
b28=4*exp(-(y(37)+65)/18);
b29=1/(1+exp(-0.1*(y(37)+35)));
b30=0.125*exp(-(y(37)+65)/80);
b31=4*exp(-(y(41)+65)/18);
b32=1/(1+exp(-0.1*(y(41)+35)));
b33=0.125*exp(-(y(41)+65)/80);
b34=4*exp(-(y(45)+65)/18);
b35=1/(1+exp(-0.1*(y(45)+35)));
b36=0.125*exp(-(y(45)+65)/80);
b37=4*exp(-(y(49)+65)/18);
b38=1/(1+exp(-0.1*(y(49)+35)));
b39=0.125*exp(-(y(49)+65)/80);
b40=4*exp(-(y(53)+65)/18);
b41=1/(1+exp(-0.1*(y(53)+35)));
b42=0.125*exp(-(y(53)+65)/80);
b43=4*exp(-(y(57)+65)/18);
b44=1/(1+exp(-0.1*(y(57)+35)));
b45=0.125*exp(-(y(57)+65)/80);
b46=4*exp(-(y(61)+65)/18);
b47=1/(1+exp(-0.1*(y(61)+35)));
b48=0.125*exp(-(y(61)+65)/80);
b49=4*exp(-(y(65)+65)/18);
b50=1/(1+exp(-0.1*(y(65)+35)));
b51=0.125*exp(-(y(65)+65)/80);
b52=4*exp(-(y(69)+65)/18);
b53=1/(1+exp(-0.1*(y(69)+35)));
b54=0.125*exp(-(y(69)+65)/80);
b55=4*exp(-(y(73)+65)/18);
b56=1/(1+exp(-0.1*(y(73)+35)));
b57=0.125*exp(-(y(73)+65)/80);
b58=4*exp(-(y(77)+65)/18);
b59=1/(1+exp(-0.1*(y(77)+35)));
b60=0.125*exp(-(y(77)+65)/80);
b61=4*exp(-(y(81)+65)/18);
b62=1/(1+exp(-0.1*(y(81)+35)));
b63=0.125*exp(-(y(81)+65)/80);
b64=4*exp(-(y(85)+65)/18);
b65=1/(1+exp(-0.1*(y(85)+35)));
b66=0.125*exp(-(y(85)+65)/80);
b67=4*exp(-(y(89)+65)/18);
b68=1/(1+exp(-0.1*(y(89)+35)));
b69=0.125*exp(-(y(89)+65)/80);
b70=4*exp(-(y(93)+65)/18);
b71=1/(1+exp(-0.1*(y(93)+35)));
b72=0.125*exp(-(y(93)+65)/80);
dy(1)= -g1*(y(2)^3)*y(3)*(y(1)-V1)-g2*(y(4)^4)*(y(1)-V2)-g3*(y(1)-V3)+k*(y(1)-y(5))+0.35*y(97)*y(13)+A*sin(2*pi*F*t);
dy(2)= -(a1+b1)*y(2)+a1;
dy(3)= -(a2+b2)*y(3)+a2;
dy(4)= -(a3+b3)*y(4)+a3;
dy(5)= -g1*(y(6)^3)*y(7)*(y(5)-V1)-g2*(y(8)^4)*(y(5)-V2)-g3*(y(5)-V3)+k*(y(5)-y(9));
dy(6)= -(a4+b4)*y(6)+a4;
dy(7)= -(a5+b5)*y(7)+a5;
dy(8)= -(a6+b6)*y(8)+a6;
dy(9)= -g1*(y(10)^3)*y(11)*(y(9)-V1)-g2*(y(12)^4)*(y(9)-V2)-g3*(y(9)-V3)+k*(y(9)-y(13));
dy(10)= -(a7+b7)*y(10)+a7;
dy(11)= -(a8+b8)*y(11)+a8;
dy(12)= -(a9+b9)*y(12)+a9
dy(13)=-g1*(y(14)^3)*y(15)*(y(13)-V1)-g2*(y(16)^4)*(y(13)-V2)-g3*(y(13)-V3)+k*(y(13)-y(17))+0.35*y(98)*y(26)+A*sin(2
*pi*F*t)
dy(14)= -(a10+b10)*y(14)+a10;
dy(15)= -(a11+b11)*y(15)+a11;
dy(16)= -(a12+b12)*y(16)+a12;
dy(17)= -g1*(y(18)^3)*y(19)*(y(17)-V1)-g2*(y(20)^4)*(y(17)-V2)-g3*(y(17)-V3)+k*(y(17)-y(21));
dy(18)= -(a13+b13)*y(18)+a13;
dy(19)= -(a14+b14)*y(19)+a14;
dy(20)= -(a15+b15)*y(20)+a15;
dy(21)= -g1*(y(22)^3)*y(23)*(y(21)-V1)-g2*(y(24)^4)*(y(21)-V2)-g3*(y(21)-V3)+k*(y(21)-y(25));
dy(22)= -(a16+b16)*y(22)+a16;
dy(23)= -(a17+b17)*y(23)+a17;
dy(24)= -(a18+b18)*y(24)+a18;
dy(25)= -g1*(y(26)^3)*y(27)*(y(25)-V1)-g2*(y(28)^4)*(y(25)-V2)-g3*(y(25)-V3)+k*(y(25)-y(29));
dy(26)= -(a19+b19)*y(26)+a19;
dy(27)= -(a20+b20)*y(27)+a20;
dy(28)= -(a21+b21)*y(28)+a21;
dy(29)= -g1*(y(30)^3)*y(31)*(y(29)-V1)-g2*(y(32)^4)*(y(29)-V2)-g3*(y(29)-V3)+k*(y(29)-y(33));
dy(30)= -(a22+b22)*y(30)+a22;
dy(31)= -(a23+b23)*y(31)+a23;
dy(32)= -(a24+b24)*y(32)+a24;
dy(33)= -g1*(y(34)^3)*y(35)*(y(33)-V1)-g2*(y(36)^4)*(y(33)-V2)-g3*(y(33)-V3)+k*(y(33)-y(37));
dy(34)= -(a25+b25)*y(34)+a25;
dy(35)= -(a26+b26)*y(35)+a26;
dy(36)= -(a27+b27)*y(36)+a27;
dy(37)= -g1*(y(38)^3)*y(39)*(y(37)-V1)-g2*(y(40)^4)*(y(37)-V2)-g3*(y(37)-V3)+k*(y(37)-y(41));
dy(38)= -(a28+b28)*y(38)+a28;
dy(39)= -(a29+b29)*y(39)+a29;
dy(40)= -(a30+b30)*y(40)+a30;
dy(41)= -g1*(y(42)^3)*y(43)*(y(41)-V1)-g2*(y(44)^4)*(y(41)-V2)-g3*(y(41)-V3)+k*(y(41)-y(45));
dy(42)= -(a31+b31)*y(42)+a31;
dy(43)= -(a32+b32)*y(43)+a32;
dy(44)= -(a33+b33)*y(44)+a33;
dy(45)= -g1*(y(46)^3)*y(47)*(y(45)-V1)-g2*(y(48)^4)*(y(45)-V2)-g3*(y(45)-V3)+k*(y(45)-y(49));
dy(46)= -(a34+b34)*y(46)+a34;
dy(47)= -(a35+b35)*y(47)+a35;
dy(48)= -(a36+b36)*y(48)+a36;
dy(49)= -g1*(y(50)^3)*y(51)*(y(49)-V1)-g2*(y(52)^4)*(y(49)-V2)-g3*(y(49)-V3)+k*(y(49)-y(53));
dy(50)= -(a37+b37)*y(50)+a37;
dy(51)= -(a38+b38)*y(51)+a38;
dy(52)= -(a39+b39)*y(52)+a39;
dy(53)= -g1*(y(54)^3)*y(55)*(y(53)-V1)-g2*(y(56)^4)*(y(53)-V2)-g3*(y(53)-V3)+k*(y(53)-y(57));
dy(54)= -(a40+b40)*y(54)+a40;
dy(55)= -(a41+b41)*y(55)+a41;
dy(56)= -(a42+b42)*y(56)+a42;
dy(57)= -g1*(y(58)^3)*y(59)*(y(57)-V1)-g2*(y(60)^4)*(y(57)-V2)-g3*(y(57)-V3)+k*(y(57)-y(61));
dy(58)= -(a43+b43)*y(58)+a43;
dy(59)= -(a44+b44)*y(59)+a44;
dy(60)= -(a45+b45)*y(60)+a45;
dy(61)= -g1*(y(62)^3)*y(63)*(y(61)-V1)-g2*(y(64)^4)*(y(61)-V2)-g3*(y(61)-V3)+k*(y(61)-y(65));
dy(62)= -(a46+b46)*y(62)+a46;
dy(63)= -(a47+b47)*y(63)+a47;
dy(64)= -(a48+b48)*y(64)+a48;
dy(65)= -g1*(y(66)^3)*y(67)*(y(65)-V1)-g2*(y(68)^4)*(y(65)-V2)-g3*(y(65)-V3)+k*(y(65)-y(69));
dy(66)= -(a49+b49)*y(66)+a49;
dy(67)= -(a50+b50)*y(67)+a50;
dy(68)= -(a51+b51)*y(68)+a51;
dy(69)= -g1*(y(70)^3)*y(71)*(y(69)-V1)-g2*(y(72)^4)*(y(69)-V2)-g3*(y(69)-V3)+k*(y(69)-y(73));
dy(70)= -(a52+b52)*y(70)+a52;
dy(71)= -(a53+b53)*y(71)+a53;
dy(72)= -(a54+b54)*y(72)+a54;
dy(73)= -g1*(y(74)^3)*y(75)*(y(73)-V1)-g2*(y(76)^4)*(y(73)-V2)-g3*(y(73)-V3)+k*(y(73)-y(77));
dy(74)= -(a55+b55)*y(74)+a55;
dy(75)= -(a56+b56)*y(75)+a56;
dy(76)= -(a57+b57)*y(76)+a57;
dy(77)= -g1*(y(78)^3)*y(79)*(y(77)-V1)-g2*(y(80)^4)*(y(77)-V2)-g3*(y(77)-V3)+k*(y(77)-y(81));
dy(78)= -(a58+b58)*y(78)+a58;
dy(79)= -(a59+b59)*y(79)+a59;
dy(80)= -(a60+b60)*y(80)+a60;
dy(81)= -g1*(y(82)^3)*y(83)*(y(81)-V1)-g2*(y(84)^4)*(y(81)-V2)-g3*(y(81)-V3)+k*(y(81)-y(85));
dy(82)= -(a61+b61)*y(82)+a61;
dy(83)= -(a62+b62)*y(83)+a62;
dy(84)= -(a63+b63)*y(84)+a63;
dy(85)= -g1*(y(86)^3)*y(87)*(y(85)-V1)-g2*(y(88)^4)*(y(85)-V2)-g3*(y(85)-V3)+k*(y(85)-y(89));
dy(86)= -(a64+b64)*y(86)+a64;
dy(87)= -(a65+b65)*y(87)+a65;
dy(88)= -(a66+b66)*y(88)+a66;
dy(89)= -g1*(y(90)^3)*y(91)*(y(89)-V1)-g2*(y(92)^4)*(y(89)-V2)-g3*(y(89)-V3)+k*(y(89)-y(93));
dy(90)= -(a67+b67)*y(90)+a67;
dy(91)= -(a68+b68)*y(91)+a68;
dy(92)= -(a69+b69)*y(92)+a69;
dy(93)= -g1*(y(94)^3)*y(95)*(y(93)-V1)-g2*(y(96)^4)*(y(93)-V2)-g3*(y(93)-V3)+k*(y(93)-y(85));
dy(94)= -(a70+b70)*y(90)+a70;
dy(95)= -(a71+b71)*y(95)+a71;
dy(96)= -(a72+b72)*y(96)+a72;
dy(97)= 1.1*(1/(1+exp((2-y(1))/5)))*(1-y(97))-190*y(97);
dy(98)= 1.1*(1/(1+exp((2-y(13))/5)))*(1-y(98))-190*y(98);