一、说明

Voronoi 单元也称为泰森多边形。 Voronoi 图在许多领域都有实际和理论应用，主要是在科学和技术领域，但也在视觉艺术领域使用。Voronoi 图以数学家 Georgy Voronoy 的名字命名，也称为 Voronoi 镶嵌、Voronoi 分解、Voronoi 分区或 Dirichlet 镶嵌（以 Peter Gustav Lejeune Dirichlet 命名）。

在数学中，Voronoi 图是将对平面（集合）划分为多个区域的算法。在最简单的情况下，这些对象只是平面上的有限多个点（称为种子、站点或生成器）。对于每个种子，都有一个对应的优先划分区域。这种区域称为 Voronoi 单元，由平面上离该种子比其他任何点更近的所有点组成。一组点的 Voronoi 图与该组的 Delaunay 三角剖分是对偶的。

注意：点、区域、边界线成为这个算法的关键要素。

二、帝国边界划分问题

我们用一个童话故事构成思想实验。

话说，哈里发国王年事已高，厌倦朝政，因而计划将他的王国分为四份，分别由四个王子管理。于是召来宰相易普拉辛，说到：“我亲爱的宰相，我打算将王国分成四个部落，分别交给王子们统辖，如今有四个城池，分别是查兰，是哥，达玛，宿吐作为它们的都城，可是如何划分疆土我毫无主张，是真主启发我召你商议此事。”宰相思索片刻，说到：“赞美安拉，我倒是有一个谋划，请借地图叙述”，国王当即请出地图如下：

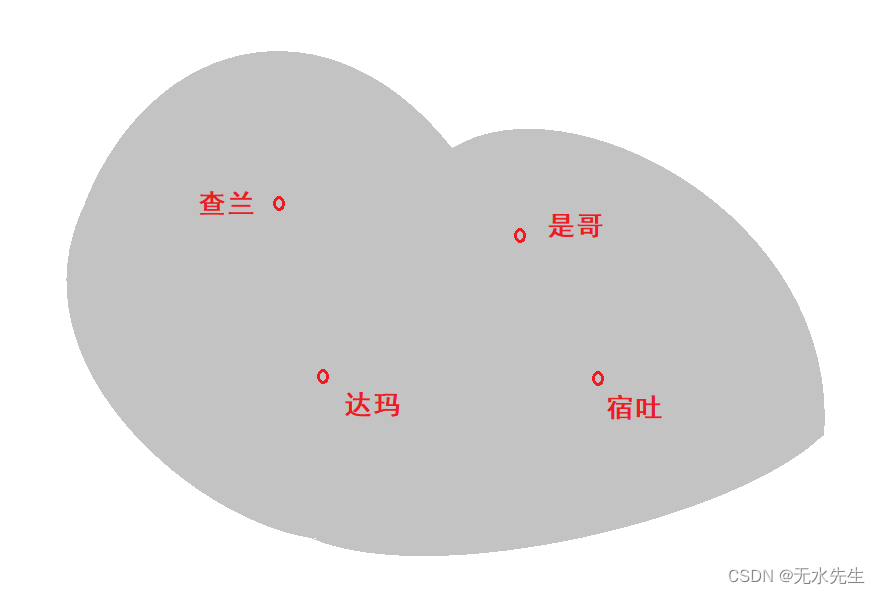
且看宰相如何划分国土。首先，确定查兰的边疆，如下：

1）从查兰引出三个线段，分别连接（是哥，达玛，宿土）

2）分别作出三条线段的中分线。

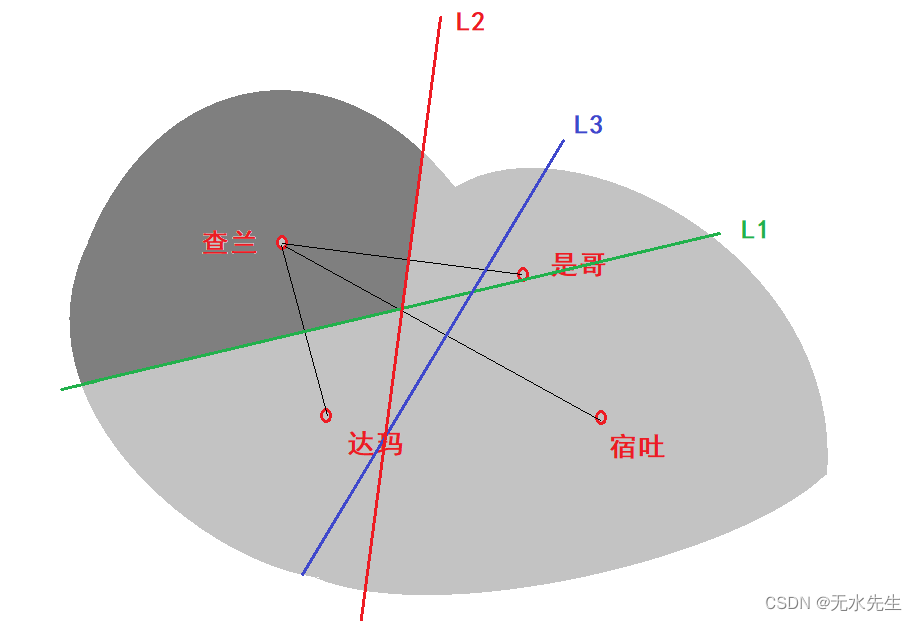
做出三条中分线L1，L2，L3。中分线上的特征是（以查兰和达玛为例），L1线上点到查兰的距离一定等于该点到达玛距离，因此谁也没“侵犯”谁。因此，绿线和红线都是“公平线”，蓝线多余，查兰的土地已经画出。

3）接着划分达玛：从达玛引出线段，连接是哥和宿土，继续上述操作：

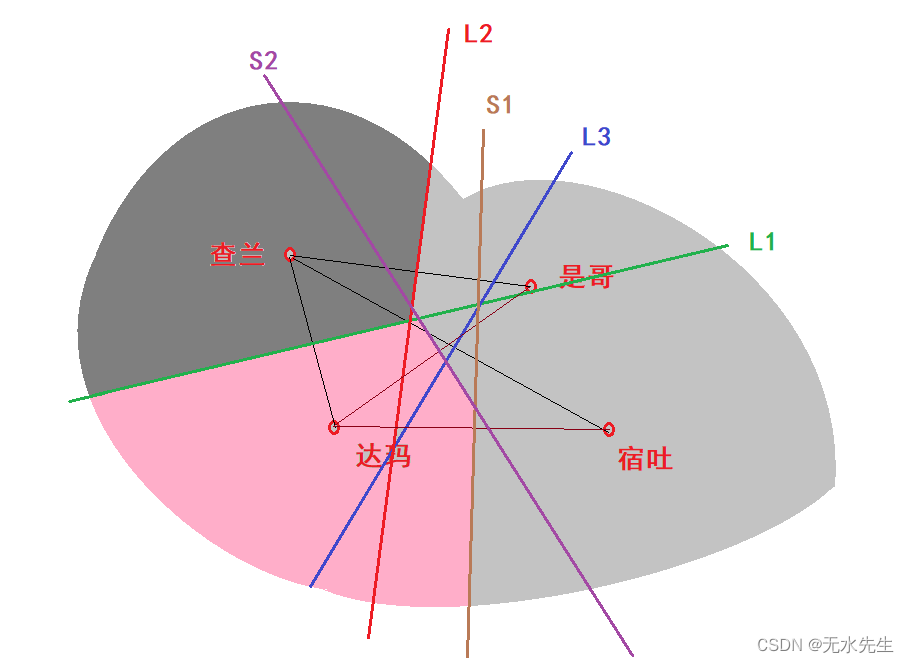
显然，图中新增出公平线S1，S2，图中的粉色（靠近达玛一侧区域）能保证达玛没有“侵犯”其它邻国。至此，达玛的边界因L1，S1，S2确定。

4）最后，从宿土到是哥引出线段，并做出中分线T1，如图：

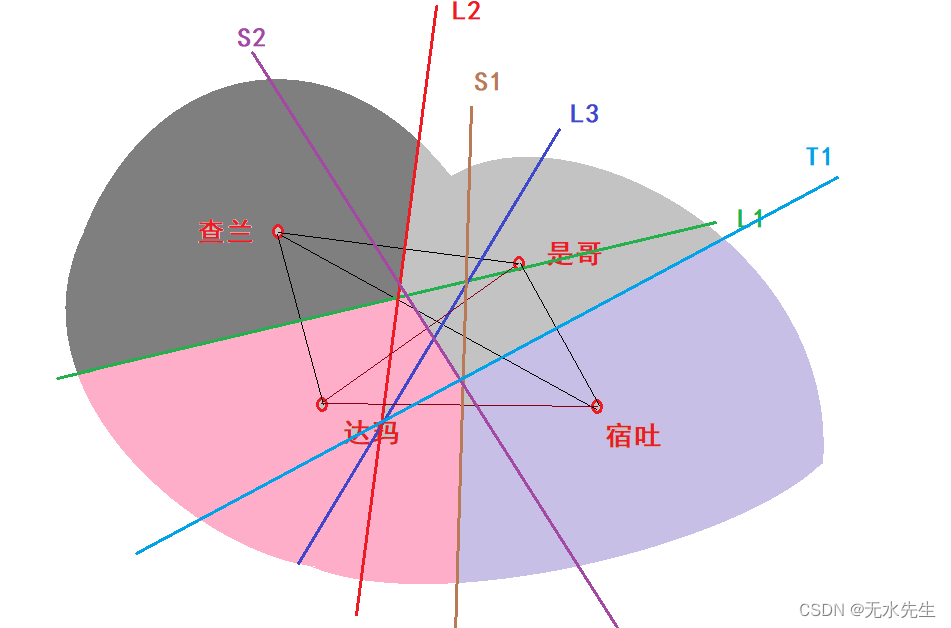
至此，宿土的边疆也因T1和S1划分完成。

哈里发看了宰相的划分，依然不悦，对宰相说到：“依照爱卿的划分，国土面积不等，如何说服四位王子服从分配？”宰相说到：“安啦是唯一的主，不妨把命运交给安拉，让他们抓阄分配”，国王听后，大喜曰：“然”。

三、voronoi的正规定义

3.1 最简单的voronoi情况

在最简单的情况下，如第一张图片所示，我们在欧几里得平面中得到一组有限的点 {p1, ..., pn}。在这种情况下，每个站点 pk 只是一个点，其对应的 Voronoi 单元 Rk 由欧几里得平面中的每个点组成，这些点到 pk 的距离小于或等于它到任何其他 pk 的距离。每个这样的单元都是从半空间的交集获得的，因此它是一个（凸）多面体。 [6] Voronoi 图的线段是平面上与最近的两个站点等距的所有点。 Voronoi 顶点（节点）是与三个（或更多）站点等距的点。

3.2 在距离空间的数学描述

设X是一个距离函数的度量空间，K是一组索引， ${\textstyle (P_{k})_{k\in K}}$ 是空间中非空子集（站点）的元组（索引集合） ${\textstyle X}$ 。 Voronoi 单元或 Voronoi 区域， ${\textstyle R_{k}}$ ，与网站相关 ${\textstyle P_{k}}$ 是所有点的集合 ${\textstyle X}$ 距离 ${\textstyle P_{k}}$ 不大于它们到其他站点的距离 ${\textstyle P_{j}}$ ，其中 ${\textstyle j}$ 是任何不同于 ${\textstyle k}$ 。换句话说，如果 ${\textstyle d(x,\,A)=\inf\{d(x,\,a)\mid a\in A\}}$ ，表示点与集合之间的距离（ ${\textstyle x}$ 和子集 ${\textstyle A}$ ），然后有：

Voronoi 图只是单元格的元组 ${\textstyle (R_{k})_{k\in K}}$ 。原则上，一些站点可以相交甚至重合（下面描述了代表商店的站点的应用程序），但通常假定它们是不相交的。此外，定义中允许有无限多个站点（此设置在数字几何和晶体学中有应用），但同样，在许多情况下，只考虑有限多个站点。

在空间是有限维欧几里德空间的特殊情况下，每个站点都是一个点，有有限多个点并且所有点都不同，那么 Voronoi 单元是凸多胞形，它们可以用组合方式表示它们的顶点、边、二维面等。有时，导出的组合结构被称为 Voronoi 图。然而，一般而言，Voronoi 单元可能不是凸的，甚至可能不是连接的。在通常的欧几里德空间中，我们可以用通常的术语重写形式定义。每个 Voronoi 多边形 ${\textstyle R_{k}}$ 与生成点相关联 ${\textstyle P_{k}}$ 。让 ${\textstyle X}$ 是欧氏空间中所有点的集合。让1个 ${\textstyle P_{1}}$ 是生成其 Voronoi 区域的点

1个 ${\textstyle R_{1}}$ ,2个 ${\textstyle P_{2}}$ 生成2个 ${\textstyle R_{2}}$ , 和3个 ${\textstyle P_{3}}$ 生成3个 ${\textstyle R_{3}}$ 等等。然后，正如 Tran 等人所表达的那样，[7]“Voronoi 多边形中的所有位置都比欧几里得平面中的 Voronoi 图中的任何其他生成点更接近该多边形的生成点”。

3.3 不同距离空间所得 Voronoi 单元不同

如图，下面是基于欧氏空间和曼哈顿空间的划分：

以上就是欧氏空间和曼哈顿空间的划分细节。

四、代码和库

4.1 算法库

以下给出算法库Voronoi，是通过python写的代码

from PIL import Image, ImageColor, ImageDraw
from random import randint, choice, random, seed as randomseed
from typing import *
from math import hypot, sqrt
from queue import Queue
from dataclasses import dataclass
from enum import Enum

import os
import sys


class ColorAlgorithm(Enum):
    random           = 1
    no_adjacent_same = 2
    least_possible   = 3


class RegionAlgorithm:
    def randomized(width: int, height: int, regions: int, mask_function) -> List[Tuple[int, int]]:
        """Return regions that are entirely random."""
        points = []
        while len(points) != regions:
            p = (randint(0, width - 1), randint(0, height - 1))

            if p in points:
                continue

            if not mask_function(p):
                continue

            points.append(p)

        return points

    def uniform(width: int, height: int, regions: int, mask_function) -> List[Tuple[int, int]]:
        """Return regions that attempt to be somewhat uniform."""
        k = 10
        points = []
        while len(points) != regions:
            best_p = None
            d_max = 0

            i = 0
            while i < k * len(points) + 1:
                p = (randint(0, width - 1), randint(0, height - 1))

                if p in points:
                    continue

                if not mask_function(p):
                    continue

                if len(points) == 0:
                    best_p = p
                    break

                d_min = float('inf')
                for x, y in points:
                    d = hypot(p[0]-x, p[1]-y)

                    if d < d_min:
                        d_min = d

                if d_min > d_max:
                    d_max = d_min
                    best_p = p

                i += 1

            points.append(best_p)

        return points


class DistanceAlgorithm:
    def euclidean(x, y, xn, yn):
        """Calculate the image regions (up to a distance) using euclidean distance."""
        return hypot(xn-x, yn-y)

    def manhattan(x, y, xn, yn):
        """Calculate the image regions using manhattan distance."""
        return abs(xn-x) + abs(yn-y)

    def euclidean45degrees(x, y, xn, yn):
        """Calculate the image regions using euclidean, but allow only lines in 45 degree increments."""
        return sqrt(2 * min(abs(xn-x), abs(yn-y)) ** 2) + abs(abs(xn-x) - abs(yn-y))

    def chebyshev(x, y, xn, yn):
        """Calculate the image regions using chebyshev distance."""
        return min(abs(xn-x), abs(yn-y)) + abs(abs(xn-x) - abs(yn-y))

    def set_each_point(seed: int, width: int, height: int,
            region_centers: List[Tuple[int, int]], image: List[List[int]],
            d_limit: int, f: List[Callable[[int, int, int, int], float]], mask_function):
        """Calculate the image regions (up to a distance) using the provided metric."""
        randomseed(seed)

        region_distance_functions = [f if not isinstance(f, list) else choice(f) for _ in range(len(region_centers))]

        for x in range(width):
            for y in range(height):
                if not mask_function((x, y)):
                    continue

                d_min = float('inf')

                for i, region in enumerate(region_centers):
                    xn, yn = region
                    d = region_distance_functions[i](x, y, xn, yn)

                    if d < d_min:
                        d_min = d

                        if d <= d_limit:
                            image[x][y] = id(region)

class Utilities:
    def error(message, q=True):
        print(f"\u001b[38;5;1mERROR:\u001b[0m {message}", flush=True)

        if q:
            sys.exit(1)

    def warning(message):
        print(f"\u001b[38;5;208mWARNING:\u001b[0m {message}", flush=True)

    def info(message):
        print(f"\u001b[38;5;11mINFO:\u001b[0m {message}", flush=True)

    def success(message):
        print(f"\u001b[38;5;2mSUCCESS:\u001b[0m {message}", flush=True)

    def hex_to_tuple(color: str):
        color = color.strip("#")
        return (int(color[0:2], 16), int(color[2:4], 16), int(color[4:6], 16))

    def get_different_adjacent_colors(width, height, image, colors, color_algorithm):
        from pulp import LpProblem, LpVariable, LpMinimize, lpSum, PULP_CBC_CMD

        edges = set()

        mapping = {}
        n = 0

        for x in range(width):
            for y in range(height):
                for xd, yd in ((0, 1), (1, 0), (-1, 0), (0, -1)):
                    xn, yn = x + xd, y + yd

                    if not 0 <= xn < width or not 0 <= yn < height:
                        continue

                    i1, i2 = image[x][y], image[xn][yn]

                    if i1 is None or i2 is None:
                        continue

                    if i1 < i2:
                        if i1 not in mapping:
                            n += 1
                            mapping[n] = i1
                            mapping[i1] = n

                        if i2 not in mapping:
                            n += 1
                            mapping[n] = i2
                            mapping[i2] = n

                        edges.add((mapping[i1], mapping[i2]))

        edges = list(edges)
        model = LpProblem(sense=LpMinimize)

        chromatic_number = LpVariable(name="chromatic number", cat='Integer')
        variables = [[LpVariable(name=f"x_{i}_{j}", cat='Binary') \
                      for i in range(n)] for j in range(n)]

        for i in range(n):
            model += lpSum(variables[i]) == 1
        for u, v in edges:
            for color in range(n):
                model += variables[u - 1][color] + variables[v - 1][color] <= 1
        for i in range(n):
            for j in range(n):
                model += chromatic_number >= (j + 1) * variables[i][j]

        if color_algorithm == ColorAlgorithm.least_possible:
            model += chromatic_number
        else:
            model += chromatic_number == len(colors)

        status = model.solve(PULP_CBC_CMD(msg=False))

        if chromatic_number.value() > len(colors):
            Utilities.error("Not enough colors to color without adjacent areas having the same one!")

        return {mapping[variable + 1]: colors[color]
                for variable in range(n)
                for color in range(n)
                if variables[variable][color].value() == 1}

    def add_border(background, border_size, read_image, write_image, width, height, mask_function):
        r = border_size // 2

        for x in range(width):
            for y in range(height):
                if not mask_function((x, y)):
                    continue

                for dx, dy in ((0, 1), (1, 0)):
                    xn, yn = x + dx, y + dy

                    if not 0 <= xn < width or not 0 <= yn < height:
                        continue

                    if not mask_function((xn, yn)):
                        continue

                    if read_image[x][y] != read_image[xn][yn]:
                        draw = ImageDraw.Draw(write_image)
                        draw.ellipse((x-r, y-r, x+r, y+r), fill=(*background,0))


def generate(
        path: str,
        regions: int,
        colors: List[Union[Tuple[int], str]],
        width: int = 1920,
        height: int = 1080,
        region_algorithm = RegionAlgorithm.uniform,
        distance_algorithm = DistanceAlgorithm.euclidean,
        color_algorithm = ColorAlgorithm.random,
        seed: Optional[int] = None,
        border_size: int = 0,
        mask: Optional[str] = None,
        mask_color = "#000000",
        animate = False,
        background = "#FFFFFF",
):
    # possibly seed the random algorithm
    if seed is None:
        seed = random()

    # possibly convert string colors to tuples
    i = 0
    while i < len(colors):
        if type(colors[i]) == str:
            colors[i] = Utilities.hex_to_tuple(colors[i])

        i += 1

    if type(mask_color) == str:
        mask_color = Utilities.hex_to_tuple(mask_color)
    elif type(mask_color) == list:
        mask_color = tuple(mask_color)

    if type(background) == str:
        background = Utilities.hex_to_tuple(background)
    elif type(background) == list:
        background = tuple(background)

    randomseed(seed)

    mask_function = lambda p: True

    if mask is not None:
        try:
            mask_img = Image.open(mask)
            Utilities.info("Mask provided.")

            w, h = mask_img.size

            mask_function = lambda p: mask_img.getpixel(p) == mask_color

            if w != width:
                Utilities.warning("Specified width doesn't match mask width, using mask width.")
                width = w

            if h != height:
                Utilities.warning("Specified height doesn't match mask height, using mask width.")
                height = h


        except Exception as e:
            Utilities.error(f"Error loading mask from '{mask}'.")

    if type(regions) == list:
        Utilities.info("Region centers provided, skipping generation.")

        # flip vertically!
        region_centers = [(int(center[0] * width), int(height - center[1] * height)) for center in regions]
    else:
        Utilities.info("Calculating region centers.")
        region_centers = region_algorithm(width, height, regions, mask_function)

    image = [[None] * height for _ in range(width)]
    Utilities.info("Calculating region areas.")
    DistanceAlgorithm.set_each_point(seed, width, height, region_centers, image, float("inf"), distance_algorithm, mask_function)

    # either assign colors randomly, or calculate the chromatic number and assign them then
    if color_algorithm == ColorAlgorithm.random:
        Utilities.info("Assigning region colors.")
        region_colors = {id(region): choice(colors) for region in region_centers}
    else:
        Utilities.info("Assigning region colors such that no two adjacent regions have the same color.")
        region_colors = Utilities.get_different_adjacent_colors(width, height, image, colors, color_algorithm)

    # if we're masking, some regions won't be assigned
    region_colors[None] = background

    # the original, full image (without borders)
    pil_image = Image.new("RGB", (width, height))
    for x in range(width):
        for y in range(height):
            pil_image.putpixel((x, y), region_colors[image[x][y]])

    if border_size != 0:
        Utilities.add_border(background, border_size, image, pil_image, width, height, mask_function)

    if animate:
        if not os.path.exists(path):
            os.makedirs(path)

        d = 1

        while True:
            animation_image = [[None] * height for _ in range(width)]
            DistanceAlgorithm.set_each_point(seed, width, height, region_centers, animation_image, d, distance_algorithm, mask_function)

            animation_pil_image = Image.new("RGB", (width, height))

            for x in range(width):
                for y in range(height):
                    animation_pil_image.putpixel((x, y), background if animation_image[x][y] is None else region_colors[image[x][y]])

            if border_size != 0:
                Utilities.add_border(background, border_size, animation_image, animation_pil_image, width, height)

            animation_path = os.path.join(path, f"{d}.png")

            animation_pil_image.save(animation_path, "PNG")
            Utilities.success(f"Animation image saved to {animation_path}")

            d += 1

            if image == animation_image:
                Utilities.success(f"Done!")
                break

    else:
        pil_image.save(path, resolution=300)
        Utilities.success(f"Image saved to {path}!")

4.2 参数说明

`generate` function arguments

path: the path (including an extension) to save the resulting file to
regions: the number of distinct regions in the diagram
colors: a list of tuples denoting the RGB of the color, or strings denoting the color in hex
width: the width of the image; defaults to 1920
height: the height of the image; defaults to 1080
region_algorithm: the algorithm that determines the centers of the regions:
- RegionAlgorithm.uniform attempts to make the centers equidistant to one another; default
- RegionAlgorithm.randomized makes the center positions entirely random
distance_algorithm: the algorithm that determines the way the distance is measured; if a list of the algorithms is provided, a random one is picked for each point
- DistanceAlgorithm.euclidean: standard euclidean distance (hypotenuse); default
- DistanceAlgorithm.manhattan: Manhattan (taxicab) distance (4 directions)
- DistanceAlgorithm.chebyshev: Chebyshev distance (8 directions)
- DistanceAlgorithm.euclidean45degrees: euclidean distance, but lines can only point in 45 degree increments
color_algorithm: the algorithm that determines the colors of the regions
- DistanceAlgorithm.random: pick the colors randomly
- DistanceAlgorithm.no_adjacent_same: pick the colors such that no two adjacent regions have the same color
- DistanceAlgorithm.least_possible: same as no_adjacent_same, but attempt to do so in the least number of colors
seed: the seed for the random number generator; no seed by default
border_size: the thickness of the border (in pixels); defaults to 0 (no border)
mask: a path to an image mask so only specific areas are used
mask_color: the color of the mask to fill, ignoring everything else; defaults to #000000
animate: creates images in the folder path of the regions filling in; defaults to False
background: background of the animation/masking/borders; defaults to #FFFFFF

4.3 调用方法

from voronoi import *

generate(
    path = "1.png",
    width = 3840,
    height = 2160,
    regions = 70,
    colors = [(0, 0, 0), (15, 15, 15), (23, 23, 23), (30, 30, 30)],
    color_algorithm = ColorAlgorithm.no_adjacent_same,
)

结果图：