目录
- 0 写在前面
- 1 什么是流形?
- 2 什么是流形学习?
- 3 等度量映射原理
- 4 Python实现
0 写在前面
机器学习强基计划聚焦深度和广度,加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理;“广”在分析多个机器学习模型:决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖,由本人亲自从底层编写、测试与文章配套的各个经典算法,不依赖于现有库,可以大大加深对算法的理解。
🚀详情:机器学习强基计划(附几十种经典模型源码)
1 什么是流形?

流形(manifolds)是可以局部欧几里得空间化的一个拓扑空间,是具有拓扑结构的点集,是欧几里得空间中的曲线、曲面等概念的推广。
欧几里得空间是最简单的流形实例。流形要求拓扑结构的局部为欧式空间或其他相对简单的空间。例如下面的左图所示,在一个半径极大的球面(如地球)上,若以充分大的尺度去度量一个三角形则其只能为曲边三角形,欧式距离不成立,因为位于二维平面上的点不能沿直线穿过球面到达目标点;若以充分小的尺度去度量则可以得到直边三角形——例如在地球上测量跑道长度无需考虑地球的曲率。下面右图中的一维流形同理

一个并非流形的实例是在球面上吊一根线,因为在包含了线和球连接的那一点的附近区域一定不是简单的——既不是线也不是面。
在流形中度量两点的距离采用测地线(geodesic),测地线是位于流形上两点的最短拓扑距离,如图所示。

2 什么是流形学习?
流形学习(manifold learning)假设样本数据分布在高维特征空间中的低维嵌入流形上,虽然整体十分复杂,但局部上仍具有欧氏空间的性质,因此可以在局部建立降维映射关系,然后再将局部映射关系推广到全局——局部线性构造全局非线性。流形学习旨在从观测样本中去寻找产生数据分布的内在本质规律,而非破坏结构性地降维。
流形学习是近年来机器学习领域的一个重要研究方向,其发展历史可以追溯到上世纪90年代。流形学习在图像处理和计算机视觉领域中被广泛应用,例如图像分割、物体识别和人脸识别等。此外,在生物信息学和医学领域中,流形学习也有很多应用,例如基因表达谱分析、疾病诊断和药物研发等。

3 等度量映射原理
等度量映射(Isometric Mapping, Isomap)是流形上的多维缩放算法,其限制样本在降维后的低维空间中的测地线距离,等价于原始空间。经典多维缩放算法原理请看机器学习强基计划8-2:详细推导多维缩放MDS算法(附Python实现)
具体算法流程如表所示

对近邻图的构建通常有两种做法:
- 指定近邻点个数,称为 k k k近邻图,例如设欧氏距离最近的 个点为近邻点;
- 指定距离阈值 ϵ \epsilon ϵ,称为 ϵ \epsilon ϵ近邻图,例如设距离小于 ϵ \epsilon ϵ的点为近邻点;
若近邻范围指定得较大,则测地线距离很远的点可能被误认为近邻——出现短路现象;若近邻范围指定得较小,则流形上部分区域可能与其他区域不存在连接,出现断路现象。短路与断路都会给后续的最短路径计算造成误导。
需注意的是, Isomap 算法只能得到训练样本在低维空间的坐标,对于新样本的预测兼容性差(需要结合回归等其他算法)。
4 Python实现
核心代码如下
def run(self, outDim):
# 获得距离矩阵
D = self.calDist()
D[D < 0] = 0
D = D**0.5
# 计算测地线距离矩阵
Dk = self.floyd(D, self.k)
# 调用多维缩放算法计算低维样本
Z = self.mds(Dk**2, outDim)
return Z
def floyd(self, D, knbrs):
maxVal = np.max(D) * 1000
Dk = np.ones((self.m, self.m)) * maxVal
DIndex = np.argsort(D, axis=1)
for i in range(self.m):
Dk[i, DIndex[i, 0:knbrs + 1]] = D[i, DIndex[i, 0:knbrs + 1]]
for k in range(self.m):
for i in range(self.m):
for j in range(self.m):
if Dk[i, k] + Dk[k, j] < Dk[i, j]:
Dk[i, j] = Dk[i, k] + Dk[k, j]
return Dk
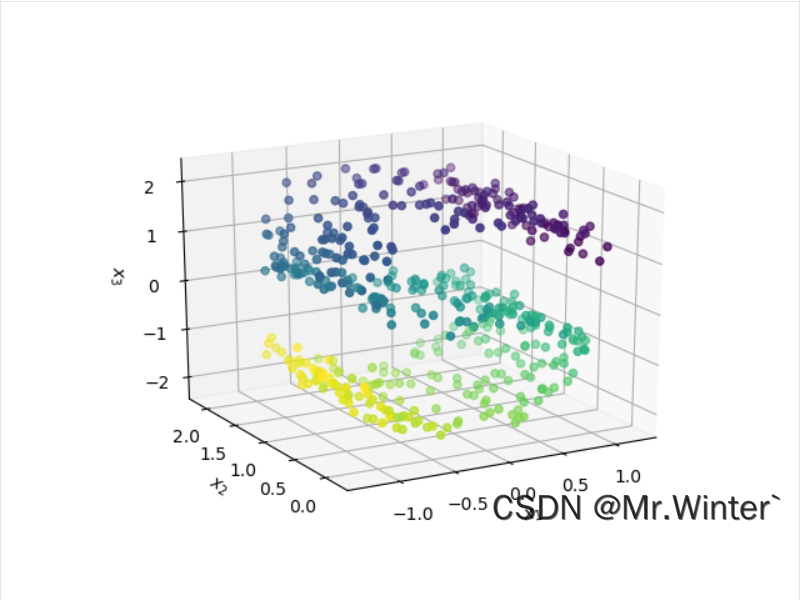
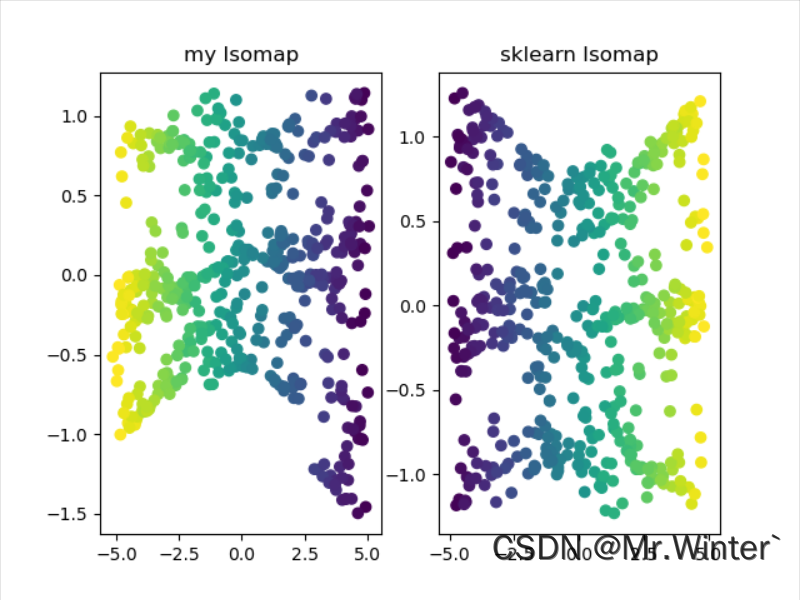
以S流形数据集为例执行降维,效果如下
本文完整工程代码请通过下方名片联系博主获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …







![「欧拉定理」[SDOI2008]仪仗队](https://img-blog.csdnimg.cn/img_convert/6e21f1e1efc4be1c3f6f034ba8e38b9e.png)