学习目标：

学习如何实现一个基于余数查商法的定点除法运算，并能够正确地进行除法计算，包括处理舍入误差和溢出等问题。具体要求包括：

熟悉定点数的表示方法和定点数的基本运算法则，理解定点除法运算的基本概念和原理。
学习余数查商法的算法流程和计算方法，并能够手动计算出除法的结果。
熟悉处理舍入误差和溢出的方法，能够正确处理各种异常情况。
使用Verilog HDL或其他硬件描述语言编写定点除法运算的模块，并进行仿真和测试，确保其能够正确地进行除法计算。
进一步优化定点除法运算的性能，例如采用查表法、位移法和乘法法等高效的计算方法，或者使用流水线和并行计算等方式提高运算速度。
实践中遇到的问题进行记录和总结，加深对定点除法运算的理解和掌握。

学习步骤：

了解基本概念和原理：首先，我会查阅相关的文献资料，了解定点除法运算的基本概念、原理和算法流程。我会学习定点除法运算的算法原理，例如余数-查商法等。
学习计算方法：在了解了基本原理后，我会开始学习具体的计算方法，包括如何进行数值计算、处理舍入误差和溢出等问题。我还会学习如何应用查表法、位移法和乘法法等常见的计算方法，以及如何在实际应用中选择合适的计算方法。
实践操作：在掌握了基本的理论知识和计算方法后，我会开始进行实践操作。这包括编写代码进行仿真和测试，调试错误并进行性能优化等。
深入研究：如果我想进一步深入研究定点除法运算，我会尝试理解其底层原理和优化方法。我会学习如何通过硬件优化、算法改进等方式提高算法的效率和精度。
不断练习和提高：最后，我会不断练习和提高自己的定点除法运算能力。我会尝试解决更加复杂的问题，学习新的技术和方法，以提高自己的水平。

2.4.1 原码除法算法原理

原码除法是一种二进制数的除法运算算法。其基本原理是将除数和被除数都转换成原码形式，然后进行一系列的移位和比较操作，最终得到商和余数。下面是原码除法算法的具体原理：

判断除数和被除数的符号，如果符号相同则结果为正，如果符号不同则结果为负。
将除数和被除数都转换成原码形式，即符号位为1表示负数，为0表示正数，其余位表示数值。例如，+3的原码为0011，-3的原码为1011。
对除数进行左移操作，使其最高位为1，直到其大于或等于被除数的绝对值。同时记录下左移的位数k。
进行一次减法操作，得到一个余数r。如果r小于除数，则继续进行一次左移和减法操作，直到r大于或等于除数。同时，记录下余数的位数i。
计算商的原码，即将k-i作为符号位，将商的绝对值作为数值位。
判断商和余数的符号是否一致，如果不一致，则需要进行补码转换。

需要注意的是，在进行原码除法时，可能会出现除数为0或被除数为最小负数的情况，需要进行特殊处理。此外，原码除法的计算速度较慢，因此在实际应用中，一般使用更为高效的补码除法算法。

恢复余数法我的理解：

恢复余数法是一种常见的除法算法，其基本思想是通过不断减去除数，直到减不下为止，得到商和余数的值。具体来说，其计算流程如下：

用除数去减被除数，如果结果小于0，则说明当前的商的最高位应该为0，被除数需要加上一个除数，然后再次用除数去减它。
如果结果大于等于0，则说明当前的商的最高位应该为1，被除数不需要做任何处理，继续用除数去减它即可。
重复执行步骤1和步骤2，直到被除数小于除数为止，此时得到的商和余数就是除法的结果。

需要注意的是，恢复余数法对于有符号数的除法计算会产生一些问题，例如在除数和被除数的符号相反时，商的符号会出现问题。因此，在实际应用中，通常会采用其他更加高效和稳定的算法，例如原码除法或补码除法等。

加减交替法我的理解：

加减交替法是一种常见的定点除法算法，其基本思想是通过不断地加减除数的倍数来逼近被除数，直到找到商和余数的值。具体来说，其计算流程如下：

将被除数和除数的绝对值都转化为二进制补码形式。
将商和余数的初始值都设置为0，并记录被除数的符号。
从高位开始依次处理每一位，对于每一位执行以下步骤：
- 将余数左移1位，并将被除数的当前位移入余数的最低位，得到当前的余数值。
- 如果余数值大于等于除数的绝对值，则说明当前的商位应该为1，余数需要减去除数的绝对值，否则当前的商位应该为0，余数不需要做任何处理。
- 如果当前正在处理被除数的符号位，或者当前余数值为0，则跳过下一位。
- 如果余数为负数，则说明商的当前位应该为0，并将余数加上除数的绝对值；如果余数为正数，则说明商的当前位应该为1，并继续进行下一位的处理。
重复执行步骤3，直到处理完所有位数，此时得到的商和余数就是除法的结果。

需要注意的是，加减交替法虽然相对简单，但是对于较大的除数和被除数，计算量会非常大，效率较低。因此，在实际应用中，通常会采用其他更加高效和稳定的算法，例如原码除法、补码除法或者高精度除法等。

两种方法的异同——我的理解

原码除法和补码除法是两种常见的定点除法算法，它们在计算过程和结果上有一些异同和优缺点。

异同点：

计算方式不同：原码除法采用除数和被除数的原码形式进行计算，补码除法采用补码形式进行计算。
商和余数的符号位不同：原码除法的商和余数的符号位和被除数的符号位一致，而补码除法的商和余数的符号位和除数的符号位一致。
计算结果不同：在被除数为负数且除数为正数的情况下，原码除法和补码除法的商和余数可能不同。

优缺点：

原码除法的优点在于实现简单，算法清晰，容易理解。但是其缺点在于商和余数的符号位与被除数一致，容易出现符号位溢出和计算错误的问题，同时在被除数为负数且除数为正数的情况下，商和余数的计算结果与补码除法不同。
补码除法的优点在于符号位的处理更加合理，结果更为准确和稳定，同时在被除数为负数且除数为正数的情况下，商和余数的计算结果与补码除法一致。但是其缺点在于实现相对复杂，需要进行多次补码转换和符号位的处理。

综合来说，在实际应用中，选择原码除法还是补码除法应该根据具体情况来决定，需要根据实际需求和系统架构的要求来进行选择。

2.4.2 并行除法器

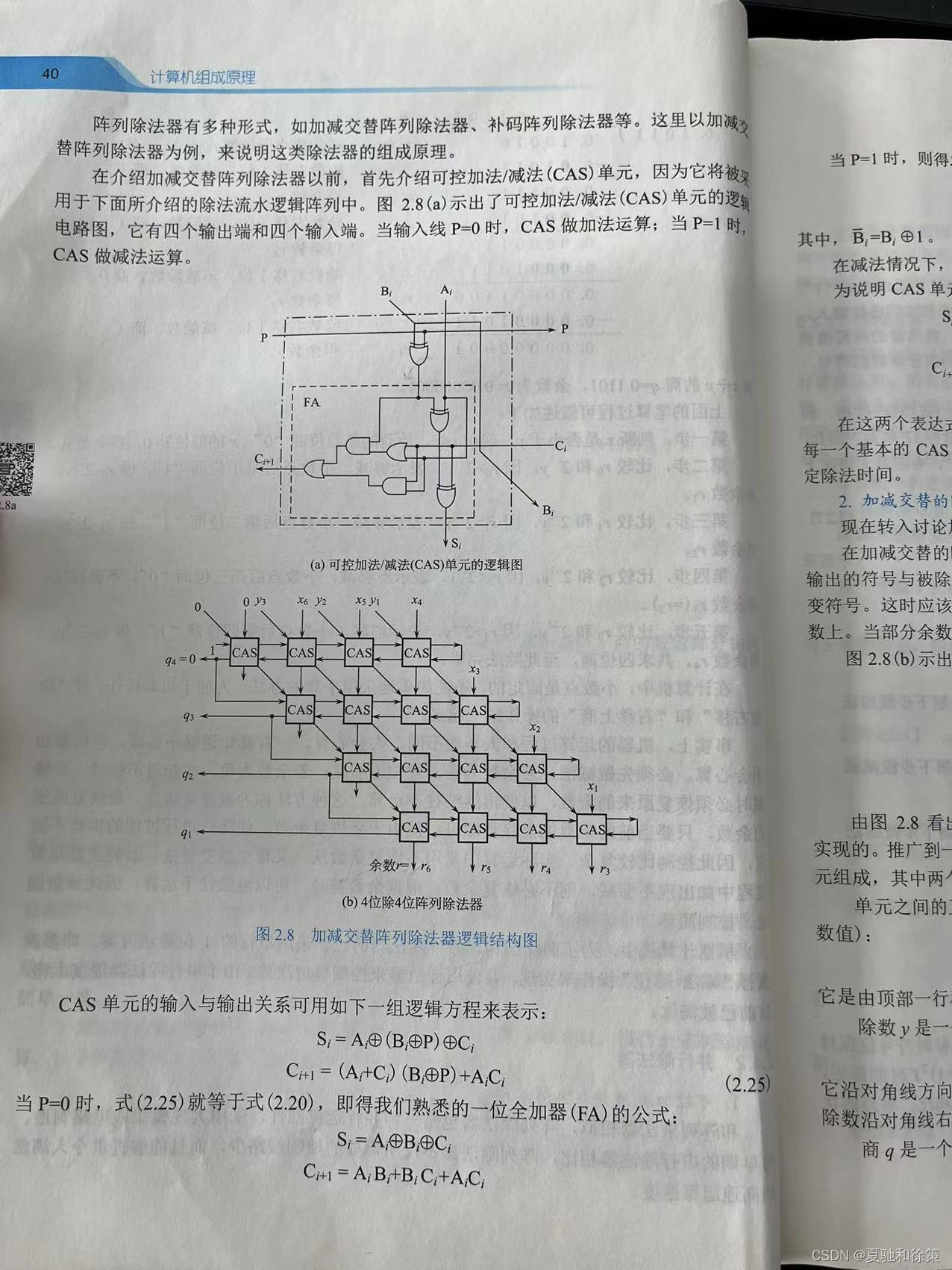
2.4.1 可控加法/减法(CAS)单元

可控加法/减法单元是一种常用的数字电路组件，它可以实现带符号整数的加法和减法运算。该单元的基本结构包括两个输入端口和一个控制端口，其中一个输入端口用于输入操作数，另一个输入端口用于输入加/减标志位，控制端口用于控制加/减操作。

可控加法/减法单元的实现通常采用门电路和选择器电路的组合。其中，门电路用于实现加法和减法的基本逻辑操作，选择器电路用于选择加法或减法的结果。在具体的实现中，可以采用多种选择器电路，如多路选择器、带使能端的选择器等。

可控加法/减法单元的主要优点是它可以实现加法和减法的转换，从而减少了电路的复杂度和成本。同时，它还可以被用作其他数字电路的基本组件，如乘法器、除法器等。

需要注意的是，在使用可控加法/减法单元时需要注意数据精度的保证和溢出的处理。此外，对于某些特殊的应用场景，如高速计算和数字信号处理等，也需要对可控加法/减法单元的性能进行优化和提高。

4.2.2 加减交替的阵列除法器

加减交替法也可以用于阵列除法器的设计中，称为加减交替的阵列除法器。它与串行除法器和并行除法器不同，采用的是一种分块计算的方式，可以加速除法的运算速度。

加减交替的阵列除法器的基本思想是，将除数和被除数分成若干个块，并将每个块分别输入到加减器中进行计算。每次计算后，将计算得到的商的低位保存到寄存器中，并将余数的高位送入下一轮计算中，以此类推，直到计算得到最终的商和余数。

在具体的实现中，加减交替的阵列除法器通常采用一个由多个可控加法/减法单元组成的阵列。在计算商和余数的过程中，加减交替的阵列除法器会将除数和被除数分成多个块，并按照从高到低的顺序输入到阵列中。在每个块的计算过程中，加减交替的阵列除法器会根据当前的加减标志位选择加法或减法运算，并通过选择器电路将计算得到的商和余数的低位保存到寄存器中。

加减交替的阵列除法器的主要优点是它能够加速除法的计算速度，并且可以并行计算每个块的商和余数，从而提高整体的计算效率。同时，它还可以采用多种优化技术，如流水线技术、交织计算等，以进一步提高计算速度。

需要注意的是，在使用加减交替的阵列除法器时，需要注意数据精度的保证和溢出的处理。此外，对于一些特殊的应用场景，如高速计算和数字信号处理等，也需要对加减交替的阵列除法器的性能进行优化和提高。