7.5 贝叶斯网

贝叶斯网亦称“信念网”，它借助有向无环图（DAG）来刻画属性之间的依赖关系，并使用条件概率表（CPT）来描述属性的联合概率分布。
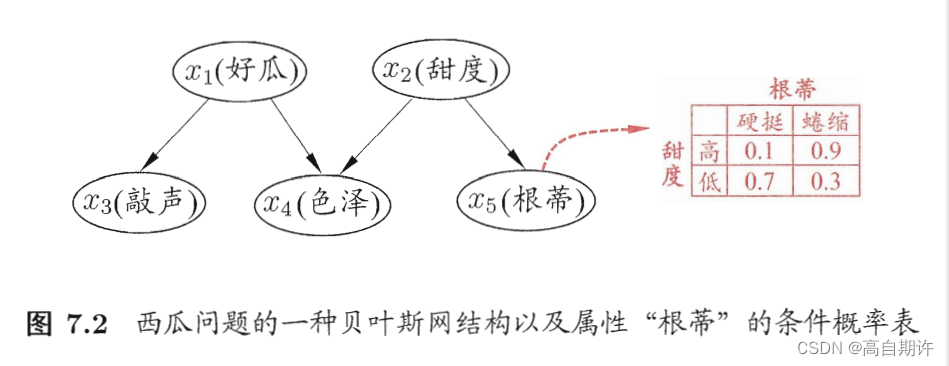
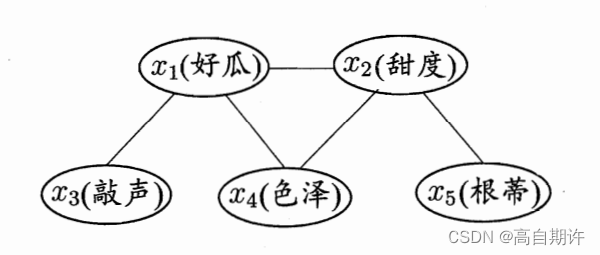
具体来说，一个贝叶斯网B由结果G和参数Θ两部分构成，即B=<G,Θ>。网络结构G是一个有向无环图，其每个结点对应于一个属性。若两个属性有直接依赖关系，则它们由一条边连接起来；参数Θ定量描述这种依赖关系，假设属性xi在G中的父节点集为Πi，则Θ包含了每个属性的条件概率表。下图以西瓜问题为例给出的一种贝叶斯网结构和属性根蒂的条件概率表。

7.5.1 结构

贝叶斯网结构有效地表达了属性间的条件独立性。给定父节点集，贝叶斯网假设每个属性与它的非后裔属性独立，于是B=<G,Θ>将属性x1,x2,…,xd的联合概率分布定义为

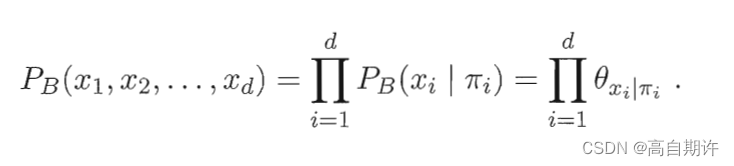
以上图为例，联合概率分布定义为P ( x1, x2, x3, x4, x5) = P(x1)P(x2)P(x3 | x1)P(x4 | x1, x2)P(x5 | x2),可以看出x3和x4在给定x1的取值时独立。x4和x5在给定x2的取值时独立。下图给出三个变量之间的典型依赖关系：

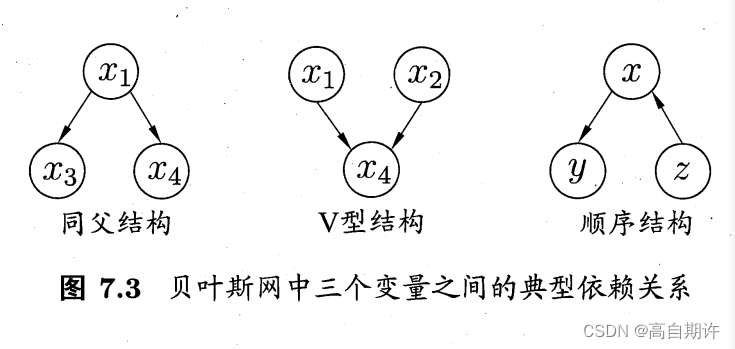
在同父结构中，给定父节点x1的值，则x3和x4独立。
在顺序结构中，给定x的值，则y与z条件独立。
在V型结构（亦称冲撞结构）中，给定x4的值，x1与x2必不独立；但若x4完全未知，则x1和x2又是相互独立的。以下是证明：

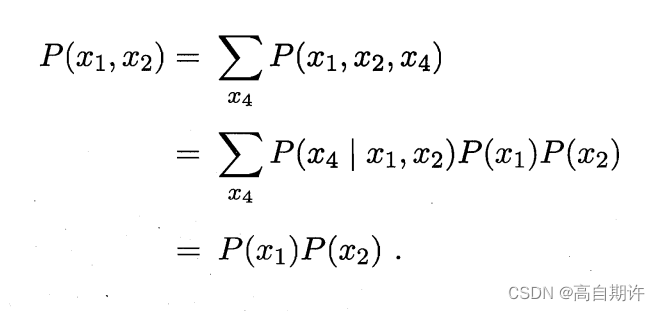
这样的独立性称为“边际独立性”。
为了分析有向图中变量间的条件独立性，可使用有向分离：
1、我们先把有向图转变为一个无向图
2、找出有向图中的所有V型结构，在V型结构的两个父节点之间加上一条无向边
3、将所有有向边改为无向边
由此产生的无向图称为道德图，令父节点相连的过程称为道德化。
下图是西瓜案例对应的道德图

7.5.2 学习

若网络结构已知，即属性间的依赖关系已知，则贝叶斯网的学习过程相对简单，只需要通过对训练样本计数，估计出每个结点的条件概率表即可。
若网络结构未知，于是贝叶斯网学习的首要任务就是根据训练数据集来找出结构最恰当的贝叶斯网。评分搜索是求解这一问题的常用办法。具体来说，我们先定义一个评分函数，以此来估计贝叶斯网与训练数据的契合程度，然后基于这个评分来寻找结构最优的贝叶斯网。
常用评分函数通常基于信息论准则，此类准则将学习问题看作一个数据压缩任务，学习的目标是找到一个能以最短编码长度描述训练数据的模型。此时编码的长度包括了描述模型自身所需要的编码位数。对贝叶斯网学习而言，模型就是一个贝叶斯网，同时，每个贝叶斯网描述了一个在训练数据上的概率分布，自有一套编码机制能使那些经常出现的样本有更短的编码。于是，我们应选择那个综合编码长度（包括描述网络和编码数据）最短的贝叶斯网，这就是最小描述长度。

7.5.3 推断

贝叶斯网训练好之后就能用来回答查询，即通过一些属性变量的观测值来推测其他属性变量的取值。通过已知变量观测值来推测待查询变量的过程称为推断，已知变量观测值称为证据。
最理想的是直接根据贝叶斯网定义的联合概率分布来精确计算后验概率，不幸的是，这样的精确推断已被证明是NP难得；
换言之，当网络结点较多，链接稠密时，难以进行精确推断，此时需借助近似推断，通过降低精度要求，在有限时间内求得近似解。在现实应用中，贝叶斯网得近似推断常使用吉布斯采样来完成，这是一种随机采样方法。

7.6 EM算法

前面的讨论均假设训练样本是完整的，现实中往往会遇到不完整的训练样本。

这就是EM算法的原型。

简要来说，EM算法使用两个步骤交替计算：
1、期望E步，利用当前估计的参数值来计算对数似然的期望值
2、最大化E步，寻找能使E步产生的似然期望最大化的参数值
然后新得到的参数值被重新被用于E步，直到收敛到局部最优解。
事实上，隐变量估计问题也可通过梯度下降等优化算法求解，但由于求和的项数将随着隐变量的数目以指数级上升，会给梯度计算带来麻烦；而EM算法则可看作一种非梯度优化方法。