数字三角形:用户登录
题目描述
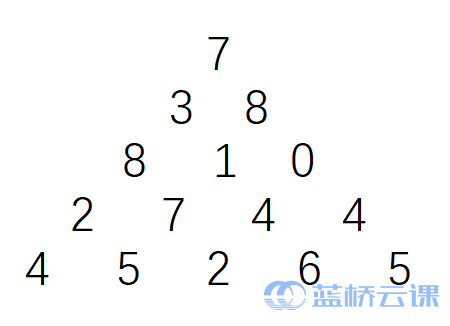
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径,把路径上面的数加起来可以得到一个和,你的任务就是找到最大的和(路径上的每一步只可沿左斜线向下或右斜线向下走)。
输入描述
输入的第一行包含一个整数 N (1≤N≤100),表示三角形的行数。
下面的 N 行给出数字三角形。数字三角形上的数都是 0 至 99 之间的整数。
输出描述
输出一个整数,表示答案。
输入输出样例
示例
输入
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出
30
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
代码:
import java.util.Scanner;
public class 数字三角形 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();//行数
int arr[][] = new int[n][n];//初始值
int dp[][] = new int [n][n];//从上到下,加上初始值
for(int i=0;i<n;i++) {
for(int j=0;j<=i;j++) {
arr[i][j] = sc.nextInt();
}
}
dp[0][0] = arr[0][0];
//先给最左边,赋加上后值
for(int i=1;i<n;i++) {
dp[i][0] = dp[i-1][0]+arr[i][0];
}
//推出每一个加上,上一个左右两侧值之后的最大值
int max=0;
for(int i=1;i<n;i++) {
for(int j=1;j<=i;j++) {
dp[i][j] = arr[i][j] + Math.max(dp[i-1][j-1],dp[i-1][j]);
if(max<dp[i][j])
max = dp[i][j];
}
}
System.out.println(max);
/*
if(n%2!=0) {
System.out.println(dp[n-1][n/2]);
}else {
System.out.println(Math.max(dp[n-1][n/2], dp[n-1][n/2-1]));
}
*/
}
}包子凑数:用户登录
题目描述
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有 N 种蒸笼,其中第i 种蒸笼恰好能放 Ai 个包子。每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买 X 个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有 X 个包子。比如一共有 3 种蒸笼,分别能放 3、4 和 5 个包子。当顾客想买 11 个包子时,大叔就会选 2 笼 3 个的再加 1 笼 5 个的(也可能选出 1 笼 3 个的再加 2 笼 4 个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有 3 种蒸笼,分别能放 4、5 和 6 个包子。而顾客想买 7 个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入描述
第一行包含一个整数 N (1≤N≤100)。
以下 N 行每行包含一个整数 Ai (1≤Ai≤100)。
输出描述
一个整数代表答案。如果凑不出的数目有无限多个,输出 INF。
输入输出样例
示例 1
输入
2
4
5
输出
6
样例说明
凑不出的数目包括:1, 2, 3, 6, 7, 11。
示例 2
输入
2
4
6
输出
INF
样例说明
所有奇数都凑不出来,所以有无限多个
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
代码:
import java.util.Scanner;
public class 包子凑数 {
static int nums[];
static int n;
static int m = 10000;
static boolean dp[];
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
nums = new int[n + 1];
for (int i = 1; i <= n; i++)
{
nums[i] = sc.nextInt();
}
// 计算最大公约数如果不为1则说明凑不出的数有无数个
int gcd = nums[1];
for (int i = 2; i <= n; i++)
{
gcd = gcd(gcd, nums[i]);
}
if(gcd != 1)
{
System.out.println("INF");
return;
}
// 有点向完全背包
// 只要能塞就疯狂塞
dp = new boolean[m + 10];
// 枚举每笼
for (int i = 1; i <= n; i++)
{
dp[nums[i]] = true;
// 枚举出重量
for (int j = 0; j + nums[i] <= m; j++)
{
if(dp[j])
dp[j + nums[i]] = true;
}
}
// 进行遍历找出没有被覆盖的地方
int ans = 0;
for (int i = 1; i <= m; i++)
{
// System.out.println(i);
if(!dp[i]) ans++;
}
System.out.println(ans);
}
public static int gcd(int a,int b)
{
if(b==0) return a;
return gcd(b, a%b);
}
}花开花落终有时,相逢相聚本无意