这是新的系列教程，在本教程中，我们将介绍使用 FPGA 实现深度学习的技术，深度学习是近年来人工智能领域的热门话题。
在本教程中，旨在加深对深度学习和 FPGA 的理解。
用 C/C++ 编写深度学习推理代码
高级综合 (HLS) 将 C/C++ 代码转换为硬件描述语言
FPGA 运行验证
在之前的文章中，我们已经依次抽取了推理核的任务并行度和循环并行度。在本文中，我们将提取推理内核的数据并行性。
数据并行
数据并行性表示待处理数据之间的并行度。
下面的代码是一个简单的向量加法运算，但是由于c[0]和c[1]计算之间没有依赖关系，所以可以同时计算。这种并行性就是数据并行性。
for (int i = 0; i < N; i++) {
c[i] = a[i] + b[i];
}另一方面，在以下处理的情况下，b[1]的值取决于b[0] ，因此在这种情况下无法提取数据并行性。
for (int i = 0; i < N; i++) {
b[i+1] = a[i] + b[i];
}补充一下和上次讨论的循环并行的区别，在循环并行中，每个进程都在一个流水线中执行。因此，上述向量相加处理的处理波形如下。
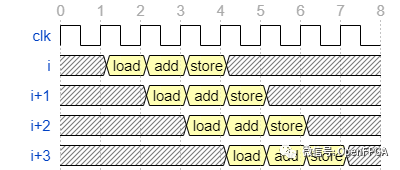
循环并行
另一方面，提取数据并行性对应于复制运算单元。复制两个计算器时的波形如下。
数据并行
处理数据并行性的难点在于，我们提取的数据并行性越多，消耗的硬件资源就越多。访问内存资源（加载/存储）特别容易出现问题。请注意，FPGA 中的 BRAM 每个周期最多只能发出 2 次加载/存储，因此如果每个周期需要超过 3 次加载/存储，则 BRAM 将加倍（如果访问目标是 BRAM）。
如下图所示，可以同时提取循环并行度和数据并行度。
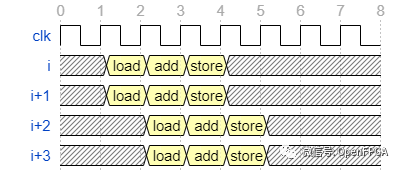
数据+循环并行
本文所有代码都是数据+循环并行的同时提取。
卷积处理中的数据并行
在卷积过程的6级循环（输出通道，y坐标，x坐标，输入通道，内核y方向，内核x方向）中可以提取出各种并行性。
在本文中，我们将提取其中两者的并行性，提高内核的性能。
首先，可以提取的并行度是下图所示的处理像素之间的并行度。
处理像素之间的并行性
由于橙色和蓝色像素的计算是相互独立的，所以它们可以同时进行。此外，用于卷积计算的内核（黄色）可以为两种计算共享。因此，一个过程（两个卷积）所需的内存访问是两次像素读取和一次内核读取。
第二种并行度是下图所示的输出通道之间的并行度。
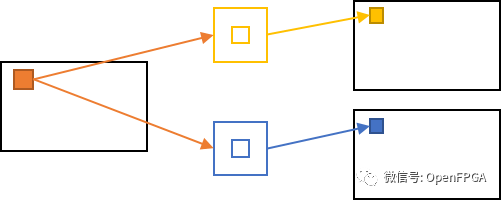输出通道之间的并行度
由于黄色和蓝色核的卷积计算是相互独立的，所以它们也可以同时进行。在这个例子中，内核需要两次读取，但像素只需要一次读取。一个进程（卷积）所需的内存访问是一次像素读取和两次内核读取。
两种并行性的图形表示如下所示。2个pixel reads和2个kernel reads可以计算出4个输出值。
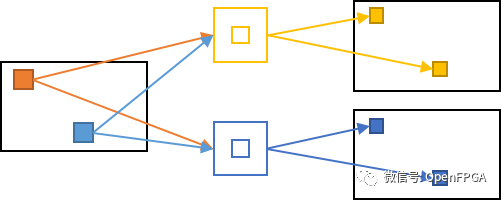处理像素之间的并行度+输出通道之间的并行度
基于此图要实现的HW框图如下。
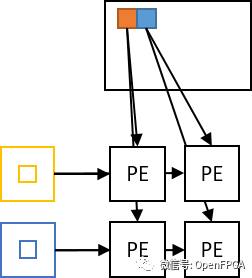卷积处理块
此处重要的是计算单元 (PE) 可以以网格模式排列。
仅对一个通道（像素/输出通道）进行数据并行化时，并行度只排列一个n算子。n前面提到，并行度的增加会导致内存资源使用量的增加，比如BRAM，在一个通道进行并行化时无法充分使用DSP。
另一方面，如上图所示，如果将两个通道并行化，则像素侧的并行度设为n，输出通道侧的并行度设为m，则总内存访问端口数相对于n+m的增加量，运算器可以排列n*m个。这样一来，FPGA中的大部分资源都可以分配给运算。许多DNN体系结构（如xDNN）都是这样同时提取多通道数据并行性的。
代码更改
由于两个通道的数据并行化是完全一样的，本文只描述两个通道并行化的结果。另外，在上一篇文章中使用移位寄存器达到了II=1，但是这里我们使用以前的版本。后面会介绍使用方法。
修改后的卷积函数如下所示：完整的代码后续会开源。
203 template <int UNROLL_X, int UNROLL_OCH>
204 static void conv2d_unrolled_v2(const float* x, const float* weight, const float* bias, int32_t width, int32_t height,
205 int32_t in_channels, int32_t out_channels, int32_t ksize, float* y) {
206
207 for (int32_t block_och = 0; block_och < out_channels; block_och += UNROLL_OCH) {
208 for (int32_t h = 0; h < height; ++h) {
209 for (int32_t block_w = 0; block_w < width; block_w += UNROLL_X) {
210 float sum[UNROLL_OCH][UNROLL_X];
211 #pragma HLS array_partition variable=sum complete dim=0
212
213 for (int32_t ich = 0; ich < in_channels; ++ich) {
214 for (int32_t kh = 0; kh < ksize; ++kh) {
215 for (int32_t kw = 0; kw < ksize; ++kw) {
216 #pragma HLS pipeline II=4
217 for (int local_och = 0; local_och < UNROLL_OCH; local_och++) {
218 #pragma HLS unroll
219 for (int local_w = 0; local_w < UNROLL_X; local_w++) {
220 #pragma HLS unroll
221 if (block_w + local_w < width && block_och + local_och < out_channels) {
222
223 int32_t och = block_och + local_och;
224 int32_t w = block_w + local_w;
...
234 float last = (ich == 0 && kh == 0 && kw == 0) ? 0 : sum[local_och][local_w];
235
236 int64_t pix_idx = (ich * height + ph) * width + pw;
237 int64_t weight_idx = ((och * in_channels + ich) * ksize + kh) * ksize + kw;
238
239 sum[local_och][local_w] = last + x[pix_idx] * weight[weight_idx];
240 }
241 }
242 }
243 }
244 }
245 }
246
247 for (int local_och = 0; local_och < UNROLL_OCH; local_och++) {
248 #pragma HLS unroll
249 for (int local_w = 0; local_w < UNROLL_X; local_w++) {
250 #pragma HLS unroll
251 if (block_w + local_w < width && block_och + local_och < out_channels) {
252 int32_t och = block_och + local_och;
253 int32_t w = block_w + local_w;
254
255 // add bias
256 y[(och * height + h) * width + w] = sum[local_och][local_w] + bias[och];
257 }
258 }
259 }
260 }
261 }
262 }
263 }主要变化如下。
1、添加模板参数UNROLL_X, UNROLL_OCH(L203)
2、将输出通道回路更改为 2 级（L207、L217、L247）
3、将 x 方向循环更改为 2 步（L209、L219、L249）
4、重复总和寄存器 (L210)
5、添加了新的编译指示unroll（L218、L220、L248、L250）
6、设置内循环管道II为4（L216）
1、添加了一个模板参数，以便可以在外部指定函数的性能。Vivado HLS / Vitis 与 C++ 模板的兼容性非常好，不仅可以像这次这样使用，还可以像这样进行设置#pragma HLS pipeline II=<TEMPLATE_VALUE>。对于习惯写Verilog HDL等的人来说，parameter几乎可以像模块语法一样使用。
2中执行的输出通道更改为 2 级，内部循环旋转了数据并行化时的并行度，local_och外部block_och循环旋转了UNROLL_OCH宽度。如果这样做，当输出通道数UNROLL_OCH不是2的倍数时，会发生数组元素之外的访问，因此需要像 L221 这样的处理。
此外，local_och循环被移动到原始代码中最内层循环的循环内kw。此更改不会影响此问题的输出，但请注意，根据正在处理的问题，可能存在更改输出的依赖项。
3和2的修改完全一样，4的求和寄存器变成了存储上述格运算单元（PE）计算结果的寄存器。
5#pragma HLS unroll是用于将数据并行性应用于循环并布置多个运算单元的编译指示。默认情况下，运算符根据循环的迭代次数重复，但factor=N可以通过提供参数来控制运算符的重复次数。
由于我们将这个 pragma 设置为local_och, local_w两个循环，所以 L223-239 中的求和操作和 L252-L256 中的偏置加法和输出操作UNROLL_W * UNROLL_OCH是重复的。看起来L239进行x, weight的加载处理也UNROLL_W * UNROLL_OCH加了1，但是由于编译器优化，每个端口UNROLL_W, UNROLL_OCH只加1。
6中设置的II=4的值就是我们在上一篇文章中看到的处理延迟。在上一篇文章中，我介绍了一种使用移位寄存器实现如下波形的技术。
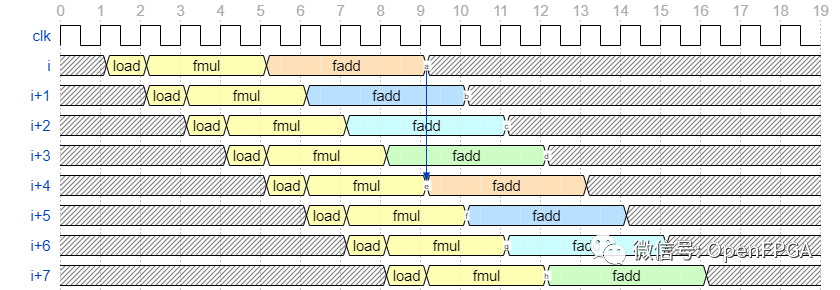
在这个例子中，我们使用了一个移位寄存器来处理每个周期切换输出目标寄存器，但是如果你像这次做数据并行化，你只需要每个周期切换数据作为计算目标。我只是更改了左侧的标签，但是如果对此进行说明，它将如下图所示。
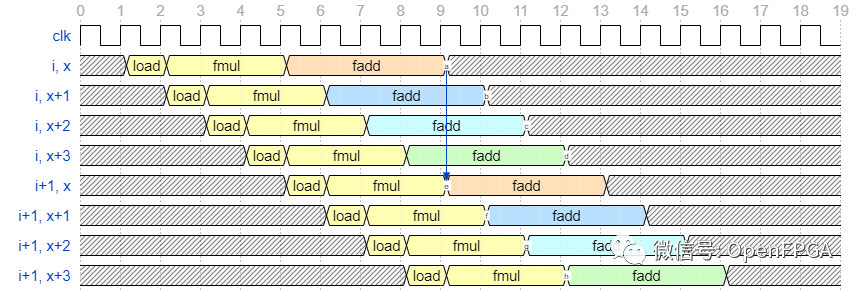
如果这样做，就不需要像上次那样需要移位寄存器之间的求和，所以效率很高。
设置 II=4 的另一个原因是x, weight端口数。它们基本上是作为 BRAM 实现的，每个周期总共允许两次读/写。由于x只是在卷积层处理的过程中被卷积层读取，所以每个周期最多可以读取2次，但是这样一来，当数据并行化的并行度设置为4时，端口数就不够用了。
由于这次II=4，当并行度为4时，每4个周期供给4个数据就足够了。它只需要 1 个读取端口，因此 BRAM 默认带宽就足够了。快速说明如果想要超过 16 度的并行度该怎么做，这可以通过#pragma HLS array_partition pragma来完成，下面附上UG902中的示意图。
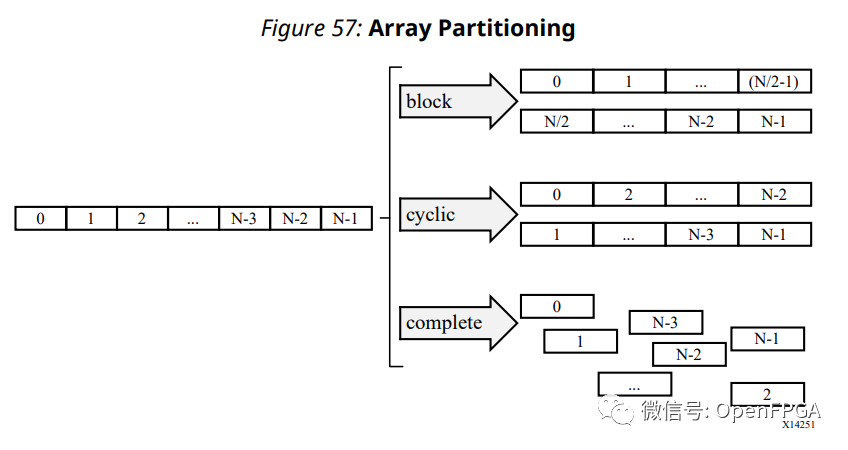
C 中定义的数组默认为 1 端口数组，如图中左侧所示。如果它像我在上一篇/这篇文章中使用的那样扩展为一个寄存器，或者如果它被并发访问，就像在这个complete循环 其实适当设置这个pragma而不降低II才是王道，但是这个pragma必须定义在数组资源（本次函数）的定义范围内，而且改变需要时间，所以这次没有使用。
综合结果/性能
使用x方向平行度为4、输出通道方向平行度为4的卷积函数综合推理函数。由于这个卷积函数如上所述有II=4，所以它每4个周期执行16次操作。在这个配置中，需要的运算单元个数为16/4 = 4，每个内存的访问端口为一个4/4 = 1端口。
查看综合结果，卷积函数中浮点运算单元资源使用量变化如下。
原始配置有两个 fadds 和一个 fmul，具有两个 fadds 的那个full_dsp_1用于添加偏差。另一方面，在数据并行化后的结果中，fadd为6，fmul为4。除了偏置加法的数量full_dsp_1增加到2之外，fadd/fmul各为4，资源量符合预期。
性能报告如下，conv2的执行时间，上篇文章时为0.423ms，加速到82.875us。
