回归的概念
回归方程:
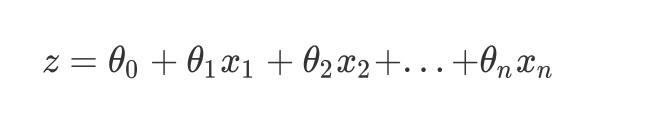
写成矩阵:
- 核心问题,构建预测函数z来映射特征矩阵x和标签y的线性关系
预测的目标值,有连续值也有离散值
- 连续值,就直接预测输出就行
- 离散值,需要在输出端加一个变换函数例如。Sigmoid函数,将连续值映射到【0,1】之间,即变成概率,根据概率大小就行判别分类
- Sigmoid函数也有致命的缺陷
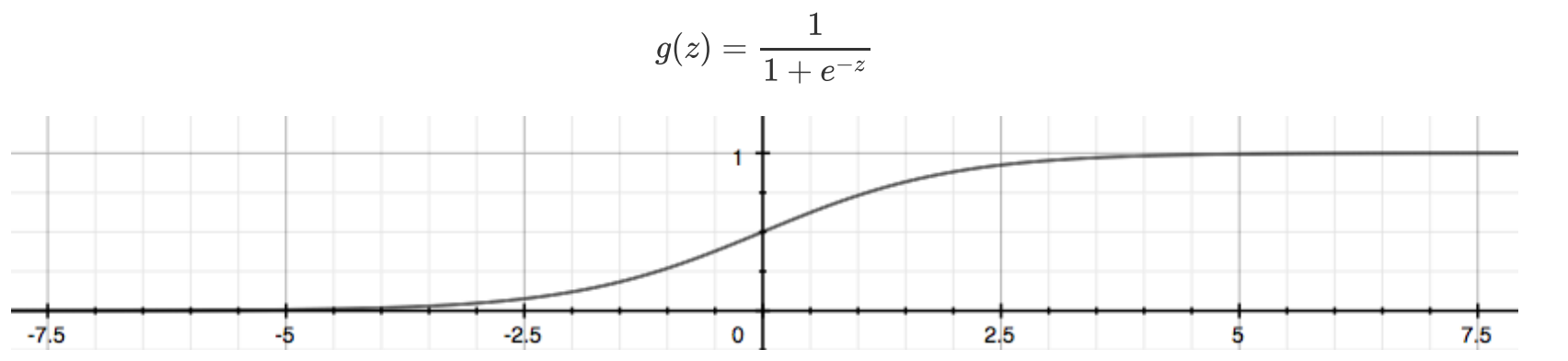
- Sigmoid函数也有致命的缺陷
- 正无穷趋近于1,负无穷趋近于0 ,会导致梯度爆炸和梯度消失
如何对标签值就行转换?
- 取对数,预测值y(x) 和 1 - y(x) 和必然为1,所以二者相除可以得到形似概率的结果

所以,叫作对数几率回归 logistic regression, 实质上在做分类
y(x)代表了样本为某一类标签的概率吗?
参考回答:

逻辑回归存在的问题
缺点:
线性回归对数据的要求很严格,比如标签必须满足正态分布,特征之间的多重共线性需要消除等等,而现实中很多
真实情景的数据无法满足这些要求,因此线性回归在很多现实情境的应用效果有限
- 逻辑回归由线性回归发展而来,当然存在这个问题
优点:
-
逻辑回归对线性关系的拟合效果好到丧心病狂。
- 特征与标签之间的线性关系极强的数据,比如金融领域中的信用卡欺诈,评分卡制作,电商中的营销预测等等相关的数据,都是逻辑回归的强项。
- 虽然现在有了梯度提升树GDBT,比逻辑回归效果更好,也被许多数据咨询公司启用,但逻辑回归在金融领域,尤其是银行业中的统治地位依然不可动摇
- 相对的,逻辑回归在非线性数据的效果很多时候比瞎猜还不如,所以如果你已经知道数据之间的联系是非线性的,千万不要迷信逻辑回归
-
逻辑回归计算快:对于线性数据,逻辑回归的拟合和计算都非常快,计算效率优于SVM和随机森林,亲测表
示在大型数据上尤其能够看得出区别 -
逻辑回归返回的分类结果不是固定的0,1,而是以小数形式呈现的类概率数字:我们因此可以把逻辑回归返
回的结果当成连续型数据来利用。- 比如在评分卡制作时,我们不仅需要判断客户是否会违约,还需要给出确定的”信用分“,而这个信用分的计算就需要使用类概率计算出的对数几率,而决策树和随机森林这样的分类器,可以产出分类结果,却无法帮助我们计算分数(当然,在sklearn中,决策树也可以产生概率,使用接口predict_proba调用就好,但一般来说,正常的决策树没有这个功能)。
详细理解

-
两种概率整合:yi的取值就是0或1 ,参数是cta
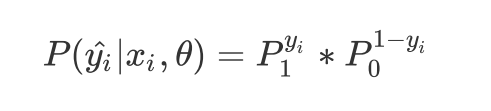
-
预测的概率P
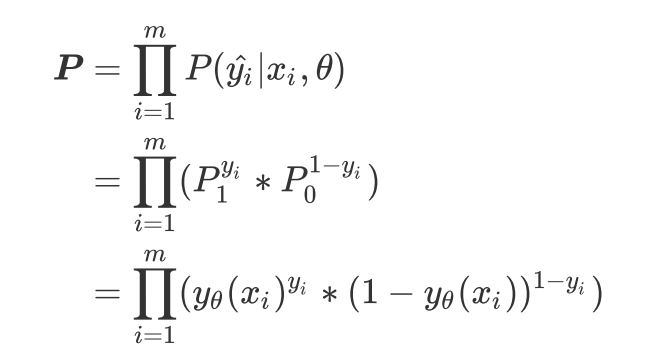
-
两边取对数
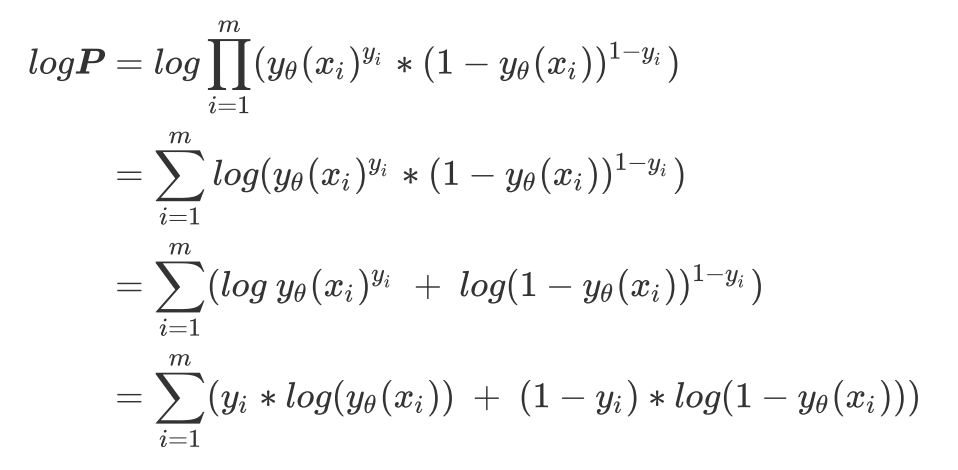
-
得到损失函数:用极大似然法推导
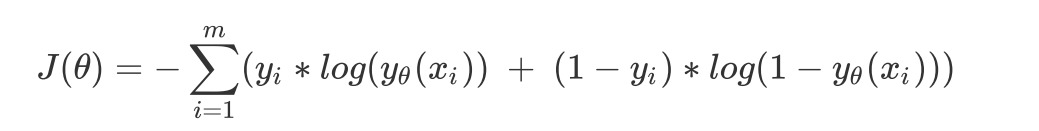
拟合:
逻辑回归和线性回归是天生欠拟合的模型,但我们还是需要控制过拟合的技术来帮助我们调整模型,对逻辑回归中过拟合的控制,通过正则化来实现。
正则化:
正则化是用来防止模型过拟合的过程,常用的有L1正则化和L2正则化两种选项,分别通过在损失函数后加上参数向
量
θ
\theta
θ 的L1范式和L2范式的倍数来实现

L1正则化:
在L1正则化在逐渐加强的过程中,携带信息量小的、对模型贡献不大的特征的参数,会比携带大量信息的、对模型
有巨大贡献的特征的参数更快地变成0,所以L1正则化本质是一个特征选择的过程,掌管了参数的“稀疏性”。L1正
则化越强,参数向量中就越多的参数为0,参数就越稀疏,选出来的特征就越少
L2正则化:
L2正则化在加强的过程中,会尽量让每个特征对模型都有一些小的贡献,但携带信息少,对模型贡献不大
的特征的参数会非常接近于0。通常来说,如果我们的主要目的只是为了防止过拟合,选择L2正则化就足够了。
逻辑回归中的特征工程
-
业务指标选择
- 直接凭借经验,选择通常相关性比较高的指标
-
PCA和SVD一般不用
- 说到降维,我们首先想到的是之前提过的高效降维算法,PCA和SVD,遗憾的是,这两种方法大多数时候不适用于
逻辑回归。逻辑回归是由线性回归演变而来,线性回归的一个核心目的是通过求解参数来探究特征X与标签y之间的
关系,而逻辑回归也传承了这个性质,我们常常希望通过逻辑回归的结果,来判断什么样的特征与分类结果相关,
因此我们希望保留特征的原貌。PCA和SVD的降维结果是不可解释的,因此一旦降维后,我们就无法解释特征和标
签之间的关系了。 - 当然,在不需要探究特征与标签之间关系的线性数据上,降维算法PCA和SVD也是可以使用的。
- 说到降维,我们首先想到的是之前提过的高效降维算法,PCA和SVD,遗憾的是,这两种方法大多数时候不适用于
-
统计方法可以使用,但不是非常必要
- 既然降维算法不能使用,我们要用的就是特征选择方法。逻辑回归对数据的要求低于线性回归,由于我们不是使用
最小二乘法来求解,所以逻辑回归对数据的总体分布和方差没有要求,也不需要排除特征之间的共线性- 解释一下特征共线性的问题:
- 在一些博客中有这样的观点:多重共线性会影响线性模型的效果。对于线性回归来说,多重共线性会影响比较大,
所以我们需要使用方差过滤和方差膨胀因子VIF(variance inflation factor)来消除共线性。但是对于逻辑回归,其实不是非常必要,甚至有时候,我们还需要多一些相互关联的特征来增强模型的表现 - 消除共线性的方法 : VIF , Box-cox方法
- 统计方法,比如方差,卡方,互信息等方法来做特征选择,也并没有问题。过滤法中所有的方法,都可以用在逻辑回归上
- 既然降维算法不能使用,我们要用的就是特征选择方法。逻辑回归对数据的要求低于线性回归,由于我们不是使用
处理:
- 直接embedding
- 方差贡献率,在逻辑回归中可以使用系数coef_来这样做
关于梯度下降的误区
对损失函数求最小值,自然而然就知道求导数,偏导数
- 注意 ∇ f ( x , y ) ∂ x \frac{\nabla f(x,y)}{\partial x} ∂x∇f(x,y), ∇ f ( x , y ) ∂ y \frac{\nabla f(x,y)}{\partial y} ∂y∇f(x,y) 其实 是对 θ \theta θ求导,然后链式求导法则来的,不是直接对x和y求偏导,得到梯度的
目标函数: J ( θ 1 , θ 2 , . . . ) , θ i ∈ θ 目标函数:J(\theta_1,\theta_2,...) ,\theta_i \in \theta 目标函数:J(θ1,θ2,...),θi∈θ
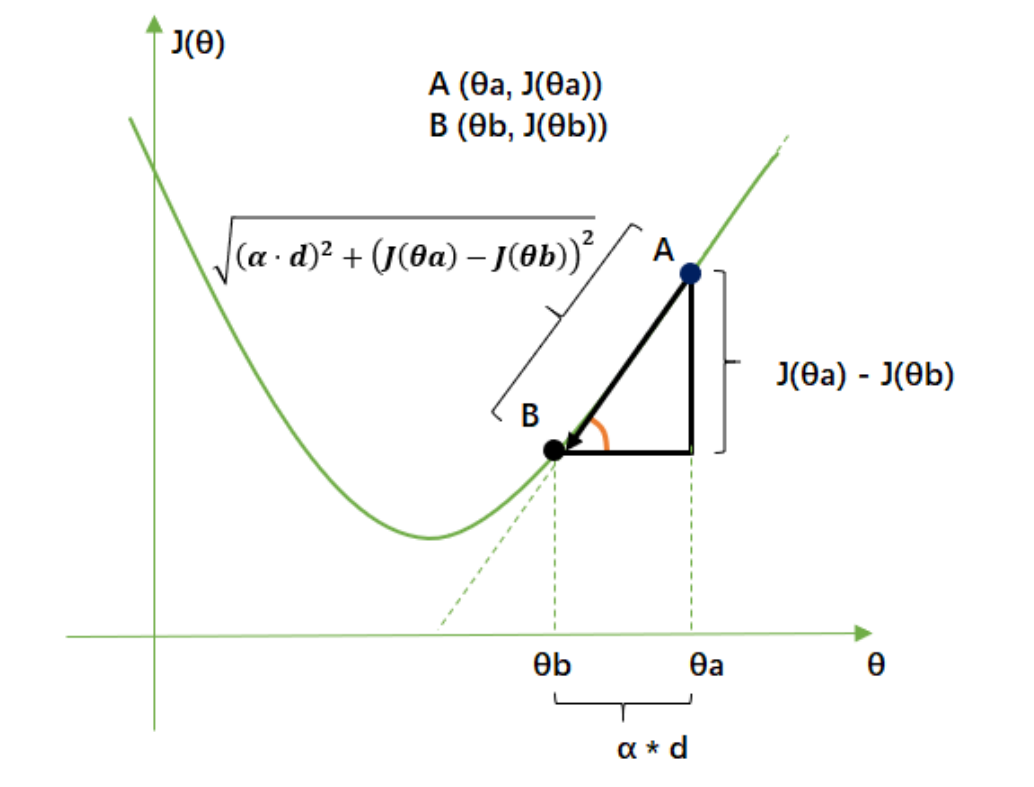
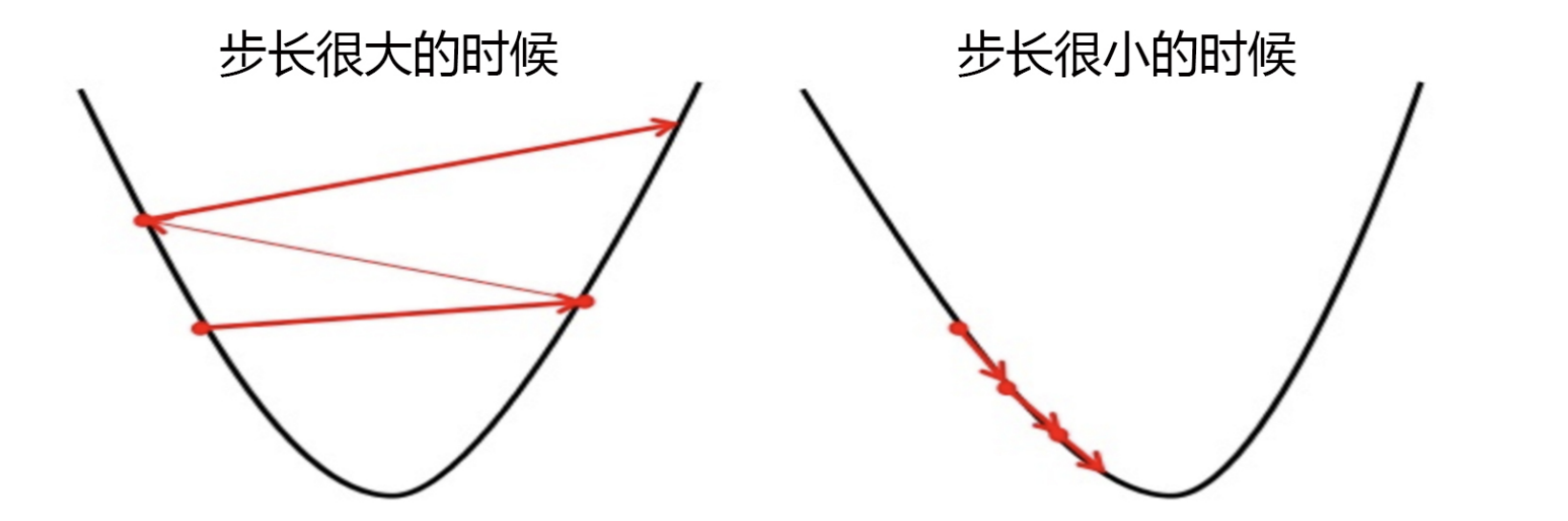
- 所以,步长不是任何物理距离,它甚至不是梯度下降过程中任何距离的直接变化,它是梯度向量的大小 d上的一个
比例,影响着参数向量 θ \theta θ 每次迭代后改变的部分。
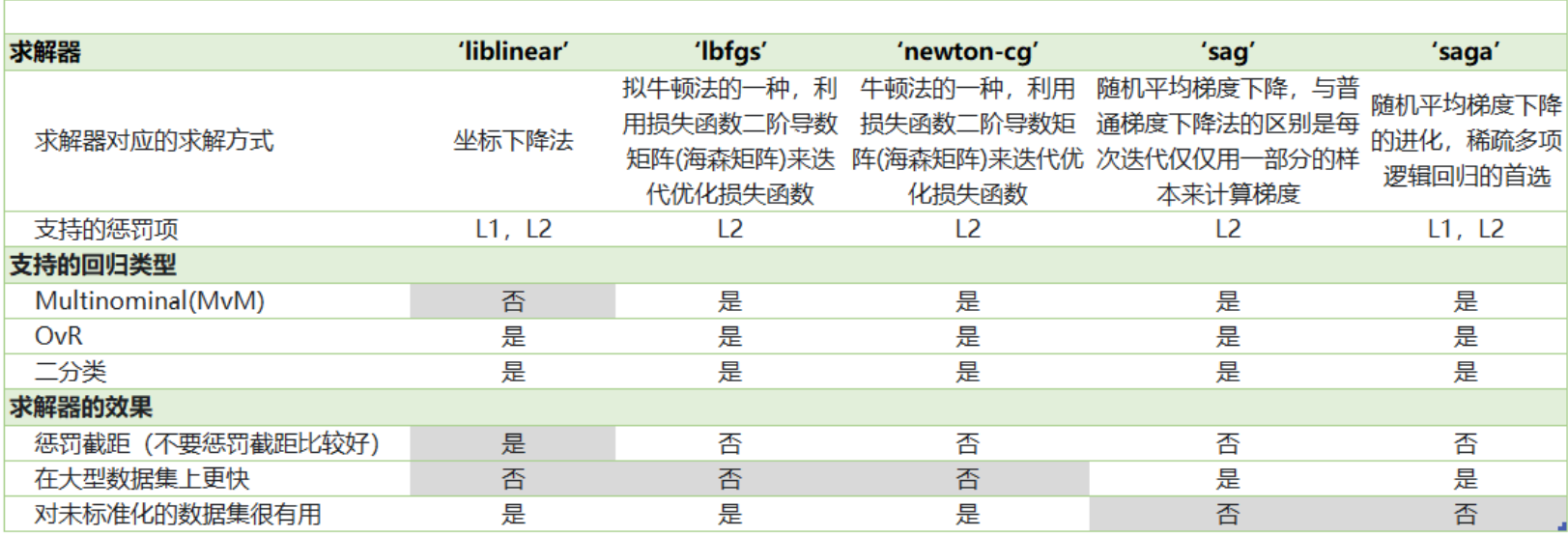
求解器
参数solver & multi_class : 二元回归与多元回归
- 样本不平衡与参数class_weight : 暂定是玄学