文章目录
- 背景
- 一、漏斗模型
- 二、漏斗模型案例
- 1. 电商购物流程
- 2. AARRR模型
- 三、如何绘制漏斗模型?
- 总结
背景
很早之前就知道漏斗模型,但没有做更多的了解和运用,后来对漏斗模型的了解稍加深入之后,觉得它不仅仅是一个模型,更是一种可以普遍适用的方法论,或者说是一种思维方式。
本文主要谈谈漏斗模型的本质、漏斗模型案例分析以及如何绘制漏斗模型。
一、漏斗模型
关于漏斗模型,我认为本质是分解和量化。为什么这么说,这里以营销漏斗模型举例。
百科给出的解释:营销漏斗模型指的是营销过程中,将非潜在客户逐步变为客户的转化量化模型。营销漏斗模型的价值在于量化了营销过程各个环节的效率,帮助找到薄弱环节。
也就是说营销的环节指的是从获取用户到最终转化成购买这整个流程中的一个个子环节,相邻环节的转化率则就是指用数据指标来量化每一个步骤的表现。
所以整个漏斗模型就是先将整个购买流程拆分成一个个步骤,然后用转化率来衡量每一个步骤的表现,最后通过异常的数据指标找出有问题的环节,从而解决问题,优化该步骤,最终达到提升整体购买转化率的目的,整体漏斗模型的核心思想其实可以归为分解和量化。
无独有偶,OKR的核心思想也是这个,即分解和量化。OKR(Objectives and Key Results)全称为“目标和主要成果”, OKR首先是设定一个“目标”(Objective),即大O,然后将该目标拆分为若干个子目标,即小O,最后将小O设定为若干个可以量化的“关键结果”(Key Results),用来帮助自己实现目标,即KRS。通过达成量化的KRS来实现小O,最终达成大O,可以看到整个过程中的核心关键也在于分解和量化。
这就是文章开头部分提到的,我觉得漏斗模型不仅仅只是一个模型,更是一种方法论,一种思维方式的原因。
可以通过这种分解和量化的形式,将问题进行不断的拆解,最后通过量化的形式来辅助达成目标,或者针对异常的步骤进行调优,最终达到总目标。
它可以广泛应用于流量监控、产品目标转化等日常数据运营工作中,称之为转化漏斗;也可以用于产品、服务销售,称之为销售漏斗。
二、漏斗模型案例
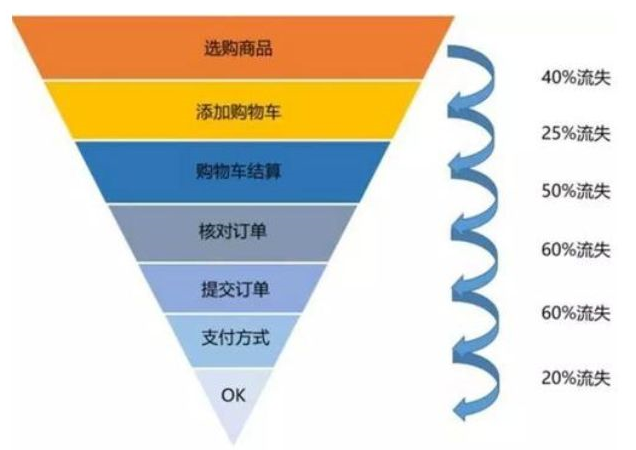
1. 电商购物流程
分析电商的转化,我们要做的就是监控每个层级上的用户转化,寻找每个层级的可优化点。对于没有按照流程操作的用户,专门绘制他们的转化模型,缩短路径提升用户体验。
2. AARRR模型
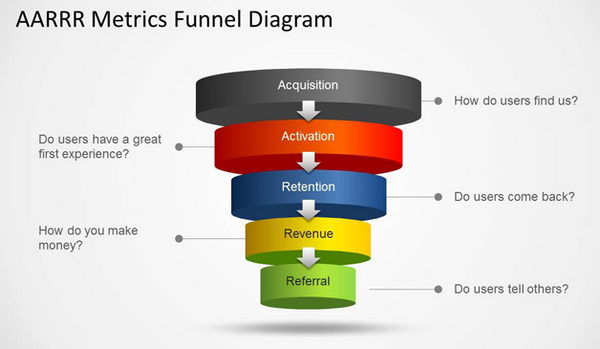
AARRR模型是指Acquisition、Activation、Retention、Revenue、Referral,即用户获取、用户激活、用户留存、用户收益以及用户传播。这是产品运营中比较常见的一个模型,结合产品本身的特点以及产品的生命周期位置,来关注不同的数据指标,最终制定不同的运营策略。
从下面这幅AARRR模型图中,能够比较明显的看出来整个用户的生命周期是呈现逐渐递减趋势的。通过拆解和量化整个用户生命周期各环节,可以进行数据的横向和纵向对比,从而发现对应的问题,最终进行不断的优化迭代。
三、如何绘制漏斗模型?
漏斗模型的绘制其实很简单,做数据报表的时候可能会用到,数据量不是很大的话,用Excel几分钟就能搞定,笔者主要介绍Python生成案例。
from pyecharts import Funnel,Grid,Bar,Page
import openpyxl
# 读取excel数据
workbook = openpyxl.load_workbook('C:\\Users\\Rose\\Desktop\\漏斗案例数据.xlsx')
sheet = workbook['工作表1']
value1 = []
title1 = sheet['A'][9].value
for cell in (sheet['B'][10:16]): #定位数据位置
value1.append(cell.value)
value2 = []
title2 = sheet['F'][9].value
for cell in (sheet['G'][10:16]): #定位数据位置
value2.append(cell.value)
value3 = []
title3 = sheet['K'][9].value
for cell in (sheet['L'][10:16]): #定位数据位置
value3.append(cell.value)
# 画图
attr = ["浏览","简历", "约面", "到面", "offer","入职"]
funnel1 = Funnel(title1,title_pos='center')
funnel1.add("漏斗",
attr,
[int(i/max(value1)*100) for i in value1],
is_label_show=True,
label_formatter='{b} {c}%',
label_pos="outside",
legend_orient='vertical', legend_pos='left',is_legend_show=False)
funnel2 = Funnel(title2,title_pos='center')
funnel2.add("漏斗",
attr,
[int(i/max(value2)*100) for i in value2],
is_label_show=True,
label_formatter='{b} {c}%',
label_pos="outside",
legend_orient='vertical', legend_pos='left',is_legend_show=False)
funnel3 = Funnel(title3,title_pos='center')
funnel3.add("漏斗",
attr,
[int(i/max(value3)*100) for i in value3],
is_label_show=True,
label_formatter='{b} {c}%',
label_pos="outside",
legend_orient='vertical', legend_pos='left',is_legend_show=False)
page = Page()
page.add(funnel1)
page.add(funnel2)
page.add(funnel3)
page
运行结果:
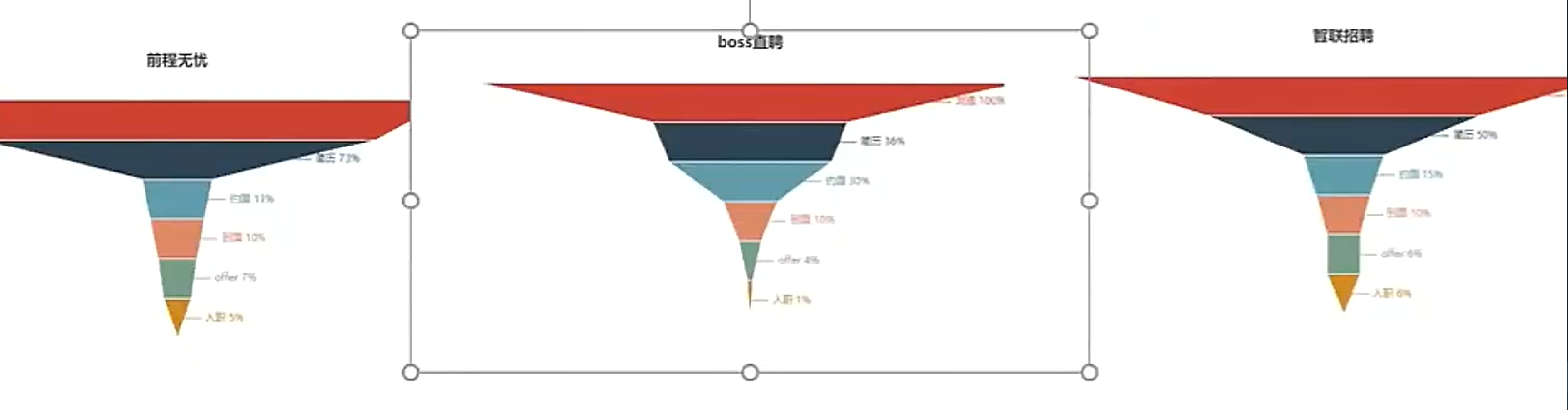
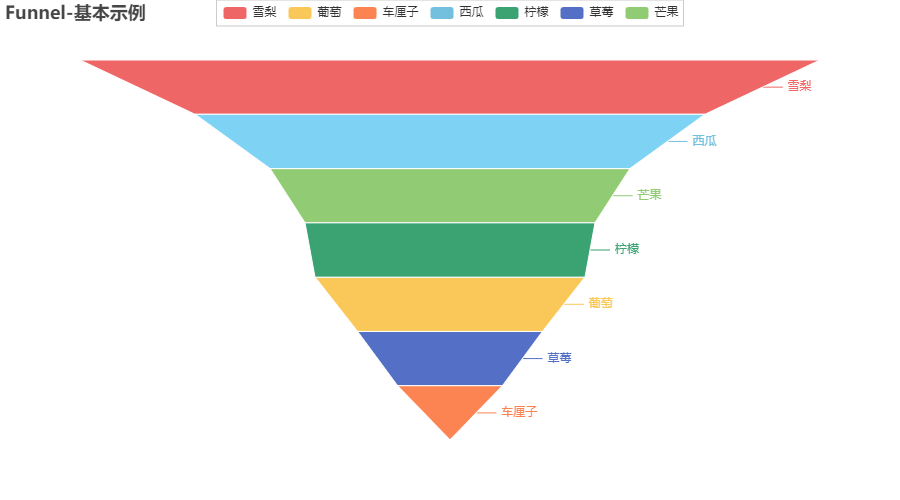
总结
当然有很多工具可以画出漏斗图,这里就不一一介绍了,pyecharts有漏斗图的模板(点击链接),套用即可。