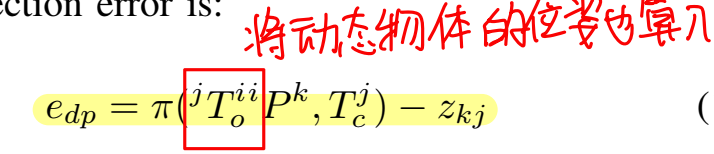一、基于单目图像的3d目标检测
这一部分是论文中最难理解的一章,作者的主要想法,是利用2d图像来生成3d的目标包围框(bounding box),一方面这个思路本身就不是很好懂,另一方面,作者写这一章还是用的倒叙,显得更难理解了。
3d包围框的定义
对于本文的3d包围框,需要使用九个量来定义,可以分为三组:位置(三维场景下的xyz坐标),旋转矩阵R(rpy一共三自由度)以及三个方向上的尺度。简单来说,3d包围框本身是一个立方体,立方体的朝向就对应旋转矩阵R,立方体中心的坐标就是位置,立方体的长宽高对应的就是三个方向上的尺度,所以一共是九个自由度来描述一个空间物体的包围框。
对于这篇论文,我们使用的是图像,所以最基础的包围框应该是2d包围框,文章的3d包围框生成都是基于假设:2d包围框同时也是3d包围框在2d平面上的投影,或者说,3d包围框的投影刚好是2d物体的最小外接矩形。在这个假设的基础上,我们需要使用消失点VP来进行物体的计算。消失点在前面MSC-VO里面也出现过,本身描述的是现实中平行的两条线,由于成像过程的畸变,导致在图像中不再是平行,而在图像中的角点,就被叫做消失点VP。
我们使用的3d包围框,本身是一个规则的立方体,最多可以同时观测到三个面,也就是做多可以计算出3个消失点,根据论文的内容,消失点的坐标可以用相机内参和物体的旋转矩阵进行计算:
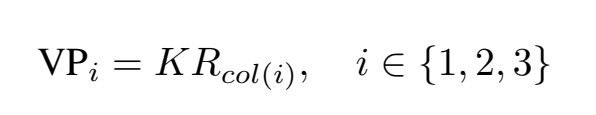
3d包围框的计算
定义好2d与3d的包围框,接下来就是如何利用2d的包围框去计算出3d的包围框,这篇文章使用的方法是采样计算后利用评分机制选择分数最高的3d包围框。根据物体的朝向,2d下的观测情况一共有三种,文章主要是以最规则的第一种进行的介绍:
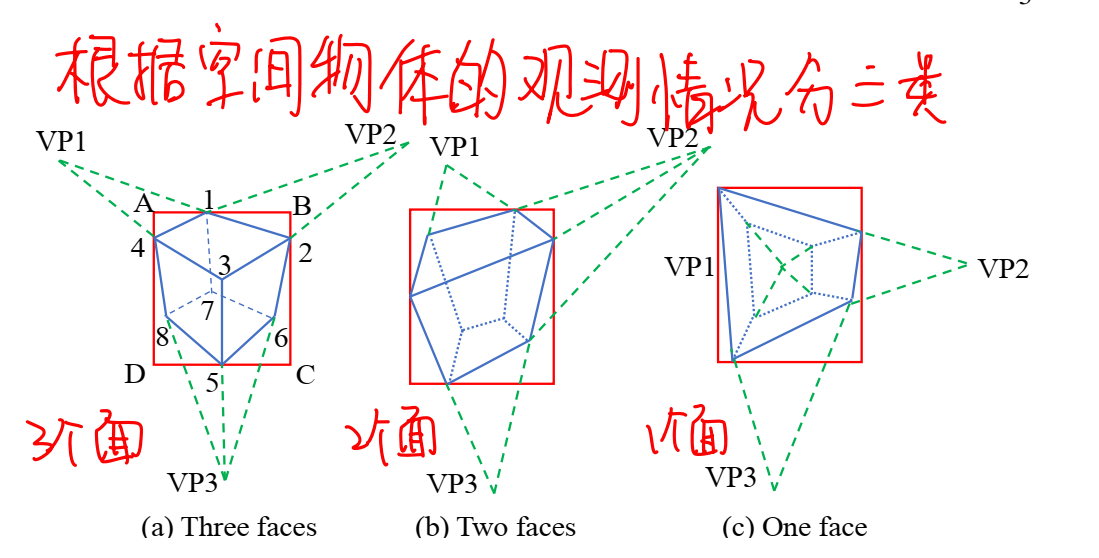
想要恢复3d的包围框,首先需要知道三个消失点以及物体投影最上方的点,也就是图a中最上面的点1,利用这四个点就可以循环计算出来剩余的2-7号点,具体来说就是用线的角点,VP1与点1可以确定一条线,这条线与BC的角点就是2号点,VP2和点1确定的线与AD的交点就是4号点,如此重复计算就可以计算出所有的点,这些点被称为2d边缘点。
得到2d边缘点之后,就可以利用这些点,重新恢复出3d包围框的边缘点,这里论文区分了两种情况:任意物体和地面上的物体。对于任意物体,恢复3d包围框主要是使用pnp进行计算,根据空间位置和当前位置的关系,可以列出3d包围框端点与2d成像平面之间的位置关系:
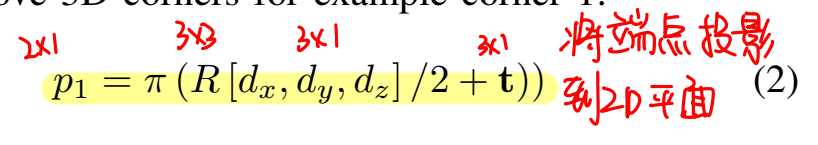
一个包围框是九个自由度,也就是说用四个点就可以解出除了尺度以外的八个自由度,所以这里使用的是八对点中随机取四个进行计算的方法。论文也没有仔细讲,为什么计算时不去考虑尺度,只说了四个点进行pnp计算,反正都是在计算,取四个点和取五个点的差别也不会太大,为什么不直接把尺度在这里一起计算。
对于在地面上的物体,由于物体一定会与地面产生联系,所以计算过程可以大大简化,也就是说物体的横滚角roll和俯仰角pitc都是0,论文说可以直接利用反投影线与地面的角点来计算与地面接触的点的坐标:

考虑到实际实现过程的复杂性,文章后续的实验全都是使用的地面物体,对于与地面没有接触的物体,论文并没有进行提取。可以看出,文章使用的2d包围框到3d包围框的计算,本身是一个比较复杂的计算过程,它需要先得到三个消失点以及最上方的2d边缘点,在此基础上才能计算出剩下的所有点,而VP的计算需要依赖于旋转矩阵R,或者说是3d包围框的朝向,朝向依赖于当前帧的位姿和相机的内参矩阵,在只考虑地面物体的情况下,3d包围框的朝向又会被进一步简化为物体的偏航角,所以说我们需要得到物体的yaw才能进行上面的一大堆计算,但是对于一个物体而言,yaw只有一个,这样说只能计算出来一个3d包围框,就不用谈后续的打分筛选机制,yaw的计算和最上方2d边缘点的计算,写在了第六章里面,yaw和最上方2d边缘点的计算都是一个采样的过程,所以会计算出来多个包围框,这才会与后续的打分机制相对应。
3d包围框的筛选
得到的多个3d包围框,我们使用一个评分标准来选择最合适的包围框,打分公式为:
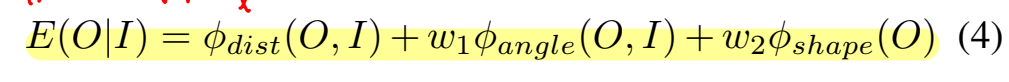
这个打分公式由三部分组成:距离偏差、角度偏差以及形状偏差。这里简单说一下这三部分偏差,只能大概看懂怎么计算,但是为什么这么计算,并不能搞清楚。距离偏差的计算,首先需要进行边缘检测和距离变换图的计算,距离变换图可以参考链接,之后对于每个可视的包围框的投影边,均匀采样十个点并在距离变换图的对应位置取和,结果除以2d包围框的对角线,以此作为距离偏差。角度偏差则是在计算场景内长线段和消失点之间的角度关系,对于一个消失点,我们可以计算出一定范围内具有最大倾斜程度和最小倾斜程度的两条线,角度偏差的计算就基于消失点和这两条线的端点:
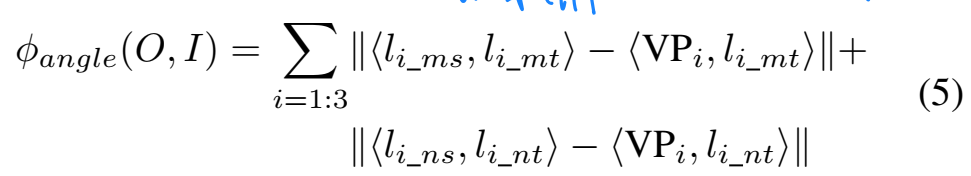
除此之外形状偏差则是最好理解的,这个误差主要是为了让3d包围框的形状更加均匀:
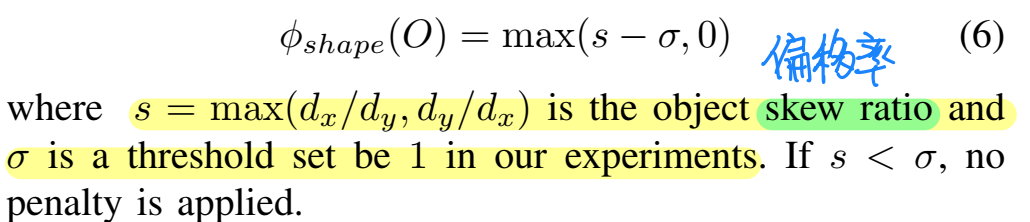
简单来说,对于这部分的2d包围框转3d包围框,首先需要得到三个消失点、最顶端的2d边缘点以及2d包围框,在此基础上,首先利用消失点和边缘点,计算出来剩余的2d边缘点,之后恢复出3d包围框的边缘点,由于消失点和边缘点的计算是基于采样的,所以会计算出来好多个3d包围框,对于这些包围框,利用打分机制,将形状、角度以及距离变换图的结果纳入考虑,从中选择最合适的包围框作为最终物体检测的结果。
二、基于物体的SLAM
在CubeSLAM里面,物体主要是用在了后端的BA优化中,也就是说,前端的跟踪还是ORBSLAM基于点的那一套,而在后端的优化中,物体作为第三个元素,与相机位姿和地图点一起进行优化。其中物体进行优化主要是指对物体包围框的位姿进行优化:

相机位姿与物体之间的约束
关于相机位姿与物体之间的约束,文章分了两种情况进行讨论,因为物体的包围框虽然是三维的,但可以通过投影转换到二维平面上,在我们比较与真实位置的偏差时,就有二维平面和三维平面两种情况。
当3d物体的检测比较准确的时候,我们使用3d的偏差,也就是将路标物体转换到相机坐标系下,然后比较相机坐标系下物体的位姿和测量值:
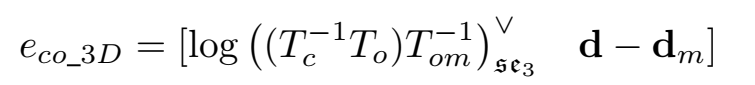
反之,如果要使用2d的偏差,那么就需要将物体投影到成像平面,比较投影位置和检测出的2d包围框之间的偏差,由于是物体向2d平面投影,所以必然会存在重叠,这里我们使用取最大值的方法去得到2d下的投影包围框:
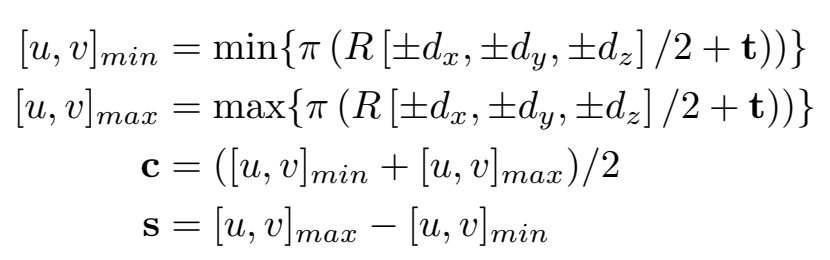
投影得到的2d包围框会与检测出来的包围框进行比较,从而得到2d的偏差:

对于这两种方法,2d偏差由于多了一个投影的过程,本身会丢失一定的信息,但反过来看我们利用2d包围框生成3d包围框的过程本身也是一个存在误差的过程,所以这两种方法没有太多纠结误差谁大谁小的意义。
物体与地图点之间的约束
物体与地图点之间的约束,主要是根据特征点相对于物体的范围,如果一个点落在了物体内部,那么这个点对应的地图点也应该在物体对应的3d包围框中:
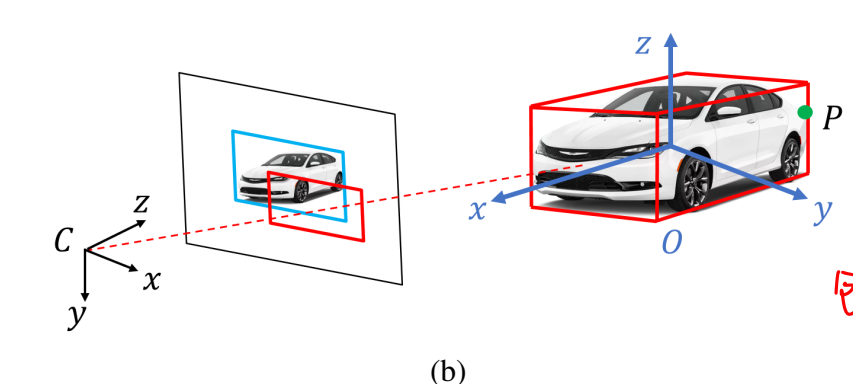
所以根据这个理论,物体与地图点之间的约束可以表示为:
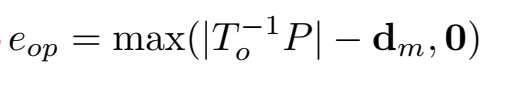
相机位姿与地图点之间的约束
这部分约束就是ORBSLAM里面的重投影误差,并没有什么改动。
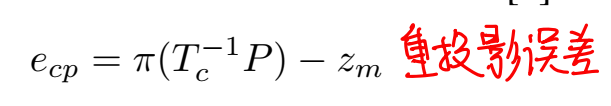
需要注意的是,物体同样需要在帧之间建立联系,相当于特征的匹配,这里使用了一个简单一些的方法,并不是对物体进行语义上的描述,而是利用其内部的特征点。具体来说,首先要将2d包围框附近的特征点与包围框建立联系,如果包围框内部的特征点能够在连续两帧内被观测到且空间坐标距离物体中心的距离不超过1m,就认为这个特征点是属于这个物体的,那么在匹配物体时,就可以利用这些特征点,如果特征点匹配数目超过阈值,就认为物体也是匹配的。
三、动态物体SLAM
一般动态特征在SLAM里面都会认为是对系统产生负面影响的特征,在CubeSLAM里面,作者单独对动态物体进行了处理,使用动态物体的运动模型来对物体包围框进行计算上的修正:
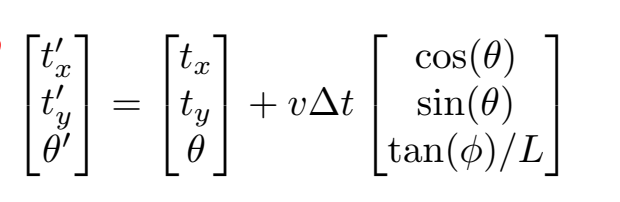
基于这种运动模型,运动物体包围框的偏差公式就变为了:

同时动态物体上的特征点也变为: