时序预测相关技术分享
时序预测是指对时间序列数据进行预测,以预测未来的趋势或行为。在实际生产和应用中,时序预测广泛应用于金融、电力、交通等领域。时序预测可以帮助人们更好地理解和掌握未来的趋势和规律,从而做出更明智的决策。
时序预测技术的方法和模型多种多样,下面介绍一些常用的方法和模型:
时间序列的基本特征
时间序列特征分解
Why
时间序列分解是一种用于分解时间序列成不同成分的方法,通常将时间序列分解为三个部分:趋势、季节性和残差。这种方法可以帮助我们更好地理解时间序列中的不同成分,从而更好地进行预测和分析。
What
- 趋势:指时间序列在较长一段时间内呈现出来的持续向上或者持续向下的变动
- 季节性:指时间序列在一年内重复出现的周期性波动,如气候条件、生产条件、节假日等
- 残差:也称为不规则波动,指除去趋势、季节性、周期性外的随机波动。不规则波动通常总是夹杂在时间序列中,致使时间序列产生一种波浪形或震荡式的变动。只含有随机波动的序列也称为平稳序列
![[图片]](https://img-blog.csdnimg.cn/8c1d7aa58ed344fdbfdabbd3ab4de6c9.png)
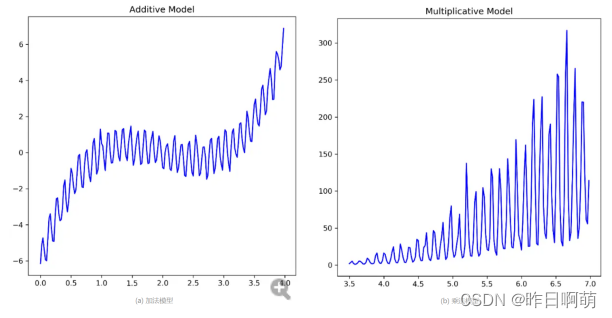
时间序列的加法模型和乘法模型是两种常用的时间序列分解方法,可以将时间序列分解为趋势、季节性、周期性和随机性四个组成部分。加法模型假设这四个组成部分相加得到时间序列,适用于时间序列的方差不随着时间序列的值而变化的情况。乘法模型假设这四个组成部分相乘得到时间序列,适用于时间序列的方差随着时间序列的值而增加的情况
![[图片]](https://img-blog.csdnimg.cn/834d4a6d487e424ebe19d46a92a39563.png)
How
具体来说,时间序列分解通常包括以下步骤:
- 移动平均或加权移动平均:通过计算序列的滑动平均或加权滑动平均来平滑序列,并去除噪声。
- 拟合趋势:根据移动平均或加权移动平均的结果来估计序列的趋势成分。常用的方法包括线性趋势、多项式趋势和指数趋势等。
- 拟合季节性:通过计算序列在每个季节内的平均值或其他统计量来估计序列的季节性成分。
- 计算残差:将序列的原始值减去拟合趋势和季节性成分的值,得到序列的残差成分。
通过这些步骤,我们可以将时间序列分解为趋势、季节性和残差三个成分,从而更好地理解序列的结构和变化规律,并进行预测和分析。
时间序列的平稳性
Why
类似于机器学习里的独立同分布假设,对于时序预测的问题,一般也有一个时间序列平稳性的前提。白话来说就是在做时间序列预测的时候,需要发现这个时间序列有规律可循。如果数据一点规律也没有,就很难建立起一个模型满足要预测的数据,因此,时间序列要有一定的趋势,形态能平稳的延续下去,才能够被很好的拟合和预测。这就是为什么有时候需要做差分平稳数据和使用ADF检验数据的平稳性。
What
平稳性的思想是时间序列的统计特性不随着时间改变而发生显著变化,如均值、方差、协方差等。
严平稳:时间序列中任意长度的两段子序列都满足相同的概率分布和联合概率分布,与时间起点选择无关。时间序列的所有统计特征都不会随着时间的推移而发生变化,概率分布不随时间的改变而改变。例如:白噪声满足标准正态分布,期望始终为0,方差始终为1,协方差都是0。
由于很难找到一个序列满足严平稳的要求,因此当数据满足弱平稳性,我们也认为它平稳。弱平稳只需要满足均值平稳和自协方差平稳即可。
How
为了判断一个时间序列是否平稳,可以通过观察序列的时序图和自相关图等方法。若时序图呈现出明显的趋势或季节性,或者自相关图中的自相关系数衰减缓慢,表明该序列不平稳。
为了使一个不平稳的时间序列变得平稳,可以通过差分、对数转换、平滑等方法进行处理。差分是指将序列中每个数据点与前一个数据点之差作为新的序列值,反复进行直到序列平稳为止;对数转换是指将序列中每个数据点取对数,使得序列的波动幅度减小,从而使得序列平稳;平滑则是通过对序列进行加权平均,减小序列中的随机波动,从而使序列平稳。
在时间序列建模中,平稳性是一个重要的前提条件。一般来说,只有平稳序列才能够应用ARIMA模型进行预测。如果序列不平稳,则需要对序列进行处理,使其变得平稳,然后再进行建模和预测。
在时间序列分析中,通常需要检验时序的平稳性,即时间序列的统计特性在时间上是不变的。平稳性是许多时间序列模型的前提条件。以下是常见的检验时序平稳性的方法:
- 直观法:通过对时间序列图像的观察,观察其是否有趋势或周期性,来判断平稳性。
- 统计量法:使用统计学方法,通过计算时间序列的统计量,来判断其平稳性。常见的统计量包括:
- 均值和方差:均值和方差应该在时间上保持不变。
- 自相关函数(ACF)和偏自相关函数(PACF):ACF和PACF应该随着时间的变化而衰减,并在某个点之后截断。
- Dickey-Fuller单位根检验:DF检验是一种常见的检验时序平稳性的方法。其原假设为序列具有单位根,即不平稳,如果p值小于0.05,就拒绝原假设,即认为序列是平稳的。
- 单位根检验:单位根检验(unit root test)是一种检验时间序列是否具有单位根的统计方法。在时间序列分析中,单位根意味着序列存在随时间变化的趋势,即序列不是平稳的。单位根检验的目的是检验序列中的单位根是否存在,从而确定序列是否具有趋势性。如果序列具有单位根,则需要进行差分处理以使序列平稳化,才能进行后续的时间序列分析和建模。常见的单位根检验方法包括ADF、KPSS等。
总之,对于时间序列的平稳性检验,需要综合使用多种方法来判断,以确保结果的可靠性。
Adfuller检验(Augmented Dickey-Fuller test)是用来检验时序数据是否平稳的一种常用方法。它可以用来检验时序数据是否具有趋势性(trend)和周期性(seasonality)。
在Adfuller检验中,它会假设时序数据的基本形式为:
y
t
=
ρ
y
t
−
1
+
ϵ
t
y_t = \rho y_{t-1} + \epsilon_t
yt=ρyt−1+ϵt
其中,
ρ
\rho
ρ 是回归系数,
ϵ
t
\epsilon_t
ϵt 是误差项。如果
ρ
=
1
\rho=1
ρ=1,则表明时序数据存在单位根,即时序数据不具备平稳性,有趋势性和周期性。
在检验时序数据的周期性方面,一种方法是对时序数据进行季节性差分(seasonal differencing),即将时序数据减去该数据在同一个季节上一年的值。如果对季节性进行差分后,数据变得更平稳,则表明时序数据具有季节性。否则,时序数据可能不具有季节性。
需要注意的是,Adfuller检验只是用来初步判断时序数据是否平稳,需要结合实际情况进一步分析。例如,即使时序数据不具有周期性,但如果存在显著的趋势,也不能将其视为平稳数据。
建模方法
对于时序预测,通常需要输出未来多个时间点的预测值,即是个多输出问题。对应的,可以将建模方式以同时输出的预测值个数分为单输出建模和多输出建模。其中细分的每一种都有其对应的训练和预测方法,也需要和固定的模型类型相结合
![[图片]](https://img-blog.csdnimg.cn/9dc0cb2d8d224476a8060cfc7d7a7d6a.png)
8个历史值与4个预测值
单输出模型
单输出建模还可以有两种方式,一种是多模型建模,一种是单模型建模。
 模型1预测y1,模型2预测y2
模型1预测y1,模型2预测y2
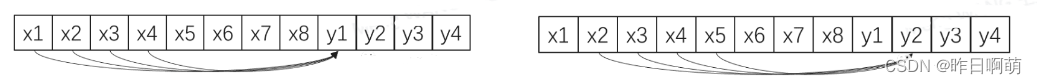
模型1预测y1,模型1预测y2
单输出模型,也称为单变量模型,是指将预测问题转化为对单一时间序列变量的预测。这种模型通常是基于历史时间序列数据,通过时间序列分析和建模方法,预测出未来的时间序列值。常用的单输出模型包括ARIMA模型、指数平滑模型等。这种模型的优点是建模简单、计算速度快,适用于单一变量的预测问题。
多输出模型
![[图片]](https://img-blog.csdnimg.cn/fd63cc1dde0c4352bcf35eda302f487a.png)
根据历史属于一次性预测y1-y4
多输出模型,也称为多变量模型,是指将预测问题转化为对多个时间序列变量的预测。这种模型考虑到多个变量之间的相互关系,通常基于多元统计分析、机器学习等方法进行建模。常见的多输出模型包括VAR模型、seq2seq等多变量模型。这种模型的优点是能够同时考虑多个变量之间的关系,更准确地预测未来值。
常用模型
基于统计的方法:
基于统计的方法是一种常见的时序预测方法,其主要思想是根据历史数据的统计规律进行预测。常用的统计方法包括移动平均模型(MA)、自回归模型(AR)、自回归积分移动平均模型(ARIMA)等。下面介绍几种常用的基于统计的时序预测模型:
- 移动平均模型(MA):移动平均模型是一种基于平均数的模型,它通过对时间序列数据的移动平均数进行预测。移动平均模型可以分为简单移动平均模型(SMA)和加权移动平均模型(WMA)两种。SMA模型只是简单地对过去n个时间点的数据取平均数,而WMA模型则对过去n个时间点的数据进行加权平均。这种方法的优点是简单易懂,但缺点是对于非平稳的时间序列不太适用。
- 自回归模型(AR):自回归模型是一种基于自身历史值的模型,它通过对时间序列数据的自身历史值进行建模预测。AR模型的基本思想是将当前时刻的值作为前几个时刻的线性组合,其中各项系数由历史数据拟合得到。AR 模型可以捕捉时间序列数据的趋势和周期性变化,但需要选定合适的滞后阶数,并且不能考虑其他因素的影响。
- 自回归积分移动平均模型(ARIMA):自回归积分移动平均模型是一种结合了AR和MA 模型和差分运算 的方法。它通过对时间序列 的差分运算 ,将非 平稳 序列 转化为 平稳 序列 ,然后再用 ARMA 模型进行预测 。 ARIMA 模式 可以应用于平稳和非平稳时间序列的预测 ,但需要选定合适 的滞后阶数 、差分次数和 移动平均阶数。 ARIMA 模式是通过寻找历史数据之间的自相关性 ,来预测未来(假设未来将重复历史的走势 ),要求序列必须是平稳的。如果序列不平稳则需要进行差分处理,而差分过程可能会导致信息丢失。、
- Prophet是一种基于加性模型的时间序列预测模型,由Facebook于2017年开源。它可以处理具有复杂季节性和趋势性的时间序列数据,并且可以自动检测和处理数据缺失和异常值。Prophet的特点是具有高度的可解释性、易于使用,并且可以快速进行大规模的时间序列预测。Prophet基于三个主要组件进行时间序列建模:趋势、季节性和假期。其中趋势组件可以是线性或非线性的,并且可以是单调或非单调的。季节性组件可以是週期性的,也可以是节假日效应,而假期组件可以包括周期性或非周期性的假期事件。
基于机器学习的方法:
这种方法是通过机器学习算法对时间序列数据进行建模和训练,以预测未来的趋势。常用的机器学习方法包括决策树、随机森林、神经网络等。树模型是一类模型,从简单的决策树到随机森林,再到现在的GBDT及其改进版本LigthGBM、Xgboost及Catboost。但是lgb等模型仅能进行单目标预测进行时序预测,所以对于多时刻预测,需要根据前述单输出的建模方式构造输入输出样本。要想使用lgb获得较好的预测效果,一个非常关键的点是特征构造。
除了结构化数据常用的一系列特征构造,时序预测有其特有的特征构造思路:
- 当前时刻值特征,比如年,月,日,小时,季度,星期,是否为节假日等,时刻值本身隐含有一些特性,比如交通流量有早高峰晚高峰,水力发电量有汛期季节性;
- 滞后特征,即历史时刻值如上一个时刻,上两个时刻,一小时前,一天前等;
- 根据滞后特征,同时可构造当前值与历史值的比值差值,不同周期的同期值比为同比,同周期的不同期值比为环比;
- 滑窗特征,体现一段连续时间内变化特性,对于单个时间窗,可做窗内统计(均值,中位数,标准差,分位数,偏度,丰度等),及窗内值与统计值交叉(如某时刻值除以一段时间内均值);
- 对于多个时间窗,可分别对各个窗进行统计并交叉,从而对整个时间段的变化进行刻画 ,等长窗如1/2/3/4号,2/3/4/5号。不等长窗如1/2/3号,1/2/3/4号,1/2/3/4/5号。
当然除了时序特征之外,还有些结构化数据通用的特征,如根据类别交叉,类别对连续值聚合统计,类别特征编码等,不在文本讨论范围内。
需要特别注意的是,树模型的外推能力十分有限,这意味着预测得到的结果基本不会超出训练集目标值范围内,也就是说,对于有显著趋势性的时间序列,树模型无法直接预测出后续持续的趋势性。那么需要先去趋势,使目标变平稳,常用有两种方法,其实都可以归结为目标变换:
- 差分,将目标值与一个固定值做差,可以是一个周期前的同期值,也可以是前一个周期内的均值、中位数等,需要根据不同问题进行尝试;
- 首先用线性回归拟合趋势,然后将目标值减去线性拟合得到的目标作为新的目标值,类似于残差预测。
基于深度学习的方法:
这种方法是利用深度学习算法对时间序列数据进行建模和训练,以预测未来的趋势。常用的深度学习方法包括循环神经网络(RNN)、长短期记忆网络(LSTM)、卷积神经网络(CNN)等。
基于深度学习的方法在时序预测问题中已经被广泛应用,下面将介绍其中的一些主要方法。
- 循环神经网络(RNN)
循环神经网络是一种适用于时序数据的神经网络,可以很好地处理时间依赖关系。常见的循环神经网络包括基础的RNN、长短时记忆网络(LSTM)和门控循环单元(GRU)等。它们可以很好地处理时间序列数据的长期依赖和非线性关系,并且可以预测多步时间序列数据。 - 卷积神经网络(CNN)
卷积神经网络主要应用于图像处理领域,但是它也可以被用来处理时序数据。在时序数据中,卷积神经网络可以用于提取局部时间特征,并且具有平移不变性。一些应用CNN进行时序预测的方法包括1D卷积神经网络和WaveNet等。 - 自注意力模型(Self-Attention)
自注意力模型是一种能够学习输入数据中不同位置之间关系的模型。在时序预测中,自注意力模型可以被用来学习时序数据中的长期依赖关系,并且可以根据不同的时间步骤来加权考虑不同的信息。 - 时空卷积网络(STCN)
时空卷积网络是一种基于卷积神经网络的方法,用于处理带有时空特征的数据。它可以同时处理时序和空间信息,并且可以自动地学习时序和空间特征之间的关系。在时序预测中,时空卷积网络可以用于处理时序数据和与之相关的空间信息,例如气象数据和地理位置数据等。
总体而言,基于深度学习的方法在时序预测中已经取得了很好的效果,但是它们通常需要大量的数据和计算资源,并且需要进行适当的调参。因此,在具体应用中需要根据实际情况选择合适的方法。
基于模型组合的方法:
这种方法是将不同的模型进行组合,以提高预测的准确性和稳定性。常用的模型组合方法包括加权平均法、堆叠法、Bagging和Boosting,Stacking等
时序预测模型融合是指将多个时序预测模型的结果结合起来,以得到更准确、更鲁棒的预测结果。常见的时序预测模型融合策略包括以下几种:
- 简单加权平均法(Simple Averaging):将多个模型的预测结果进行加权平均,权重可以是人工设置的,也可以通过交叉验证等方法进行优化。优点是简单易实现,计算速度快;缺点是需要手动设置权重,不易学习到不同模型的优点和缺点。
- 堆叠集成法(Stacking Ensemble):将多个模型的预测结果作为特征输入到一个新的模型中进行训练。这种方法可以融合多个模型的优点,并且可以根据不同的数据集和问题进行定制化设计。缺点是需要更多的计算资源和时间,容易出现过拟合问题。
- 投票集成法(Voting Ensemble):将多个模型的预测结果进行投票,取得票最多的预测结果作为最终结果。这种方法可以通过多数投票的方式抵消单个模型的误差,从而得到更加鲁棒的预测结果。缺点是对于预测结果相差较大的模型,可能会产生误导性结果。
- 权重平均法(Weighted Averaging):类似于简单加权平均法,但是权重可以通过交叉验证等方法进行优化。不同于简单加权平均法,该方法可以学习到不同模型的权重,并且可以根据不同的数据集和问题进行定制化设计。缺点是需要进行交叉验证等方法进行优化,计算成本较高。
- 贝叶斯模型平均法(Bayesian Model Averaging):利用贝叶斯方法计算多个模型的加权平均值,该方法可以将不确定性考虑在内,并且可以用于选择最佳的子集模型。缺点是需要更多的计算资源和时间,计算成本较高。
以上是常见的时序预测模型融合策略,每种方法都有其优点和局限性,具体选择哪种方法需要根据数据集和问题进行定制化设计。同时,需要注意的是,模型融合需要消耗更多的计算资源和时间,需要在准确性和效率之间进行权衡。
wavenet
WaveNet的基本思路是使用一系列不同大小的卷积核(即不同大小的感受野)来学习时域上的模式。在每个时刻,WaveNet使用一个大小为k的卷积核来预测下一个采样点的值。由于卷积核的大小是可调节的,WaveNet可以处理不同时间尺度的模式,从而能够建模长期依赖关系。同时,为了处理不同频率的信号,WaveNet还使用了“dilation causal convolutions”(膨胀因果卷积),即在卷积过程中,只使用之前的采样点进行计算,这样可以确保模型不会违反建模序列的顺序,避免信息穿越。
![[图片]](https://img-blog.csdnimg.cn/2786d276e3194663a84ba1caac1293bb.png)
什么是因果?
因果卷积其实很好理解,就是普通的卷积砍一半,补0的话补一边就可以了,补0主要是针对与深层的cnn结构,如果不补0则很难构建深层,因为每次卷积之后的feature map 不做补0则都是越卷越少的:
为什么要挖洞?
简单来说就是在不增大参数量的情况下,可以把很久之前的数据考虑进来,不过也有一个问题就是近期的数据没有考虑进来,不过没关系,浅层的时候洞挖的少一点,越深层洞越多,这样就可以把不同大小的局部信息都考虑进来了,放两个对比图
![[图片]
[图片]](https://img-blog.csdnimg.cn/b3f322e0d16d469fbe0c8e897238fd77.png)
最后使用残差和跳跃链接保证训练更深的模型
![[图片]](https://img-blog.csdnimg.cn/899186f9ad6847bd98f3246f50cfef9b.png)
WaveNet在语音合成任务上取得了很好的效果,可以生成非常自然的语音,同时在音频信号处理的其他任务上也获得了不错的表现。WaveNet的创新之处在于使用了全卷积网络结构和causal dilation技术,这些技术可以被应用到其他领域的序列建模问题中,如文本生成、机器翻译等。
相关代码参考链接:
- Run
git clone https://github.com/JEddy92/TimeSeries_Seq2Seq.git - Obtain the wikipedia web traffic data from kaggle.
Store it in a folder called “data” at the top level of this repo (this is where the notebooks point to when reading data).
参考文献
https://www.cnblogs.com/gujiangtaoFuture/articles/12171723.html
https://zhuanlan.zhihu.com/p/349897496