本文用大量的理论论述了基于解纠缠约束优化的域泛化问题。
这篇文章认为以往的文章在解决域泛化问题时所用的方法都是non-trivial的,也就是说没有作严格的证明,是不可解释的,而本文用到大量的定理和推论证明了方法的有效性。
动机
因为域泛化问题是通过在多个源域上训练模型,使模型能在目标域上获得好的效果,所以域泛化问题本质上是学习一个好的域不变语义表示模型。因此本文提出了一个解耦网络,把样本解耦成变化特征和语义特征(变化特征和语义特征是什么意思呢这个之后会详细说明),用生成器辅助语义编码器,使语义编码器能学习到域不变表示。
怎么实现域泛化:
把样本分解成Variation特征和Semantic特征。Variation可以看成是风格特征,Semantic可以看成是内容特征。
通过把样本的内容和风格分离,让Semantic编码器学习域不变表示。
具体做法:
- 输入:一组样本数量有限的数据这些数据可以来自不同源域
- Variation Encoder:学习Variation特征,也就是风格特征(比如图中学习的是旋转角度),与内容无关
- Semantic Encoder:学习语义特征,也就是类别特征,与域无关
因此两个Encoder实现了风格和类别的解耦。 - Generator:生成带有V的风格和S类别的样本
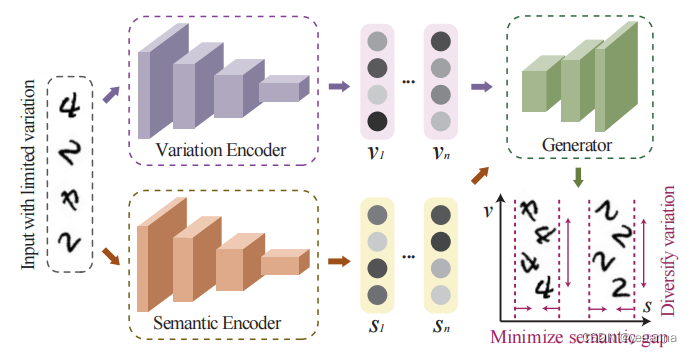
把一个样本xi输入到Semantic Encoder中,把另一个样本xj输入到Variation Encoder中,(这俩样本可能不是同一个域),让Generator学习生成带有V的风格和S类别的样本
Semantic Encoder与Generator本来是对抗关系,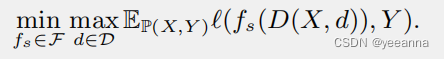
,也就是训练Decoder使损失尽可能大,训练Semantic Encoder使损失尽可能小,但这篇文章没有用到复杂的生成对抗损失,而是转换成了计算简单的约束优化问题:
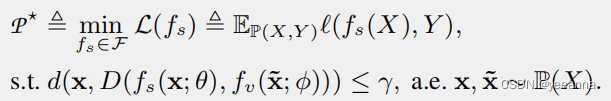
如何理解约束优化公式?
约束条件的含义:同分布样本x,x’ 经过fs和fv,输出向量,concat后输入generator里,输出的样本与原始输入到fs里的样本x的距离要小于一个约束y
对约束优化公式的解释:
我们先不看约束条件。假设没有约束条件,就是一个最简单的交叉熵损失解决分类问题。那么学习到的fs(θ)既考虑到了内容信息也考虑到了风格信息,所以没有域泛化的特点。
那么怎么才能实现域泛化?给该损失添加一个约束。根据定义1(下面有解释)可知,如果x与x’同分布,Decoder就会生成x,这样就满足约束条件。而定义1的成立是在fs对于所有的域都具有不变性的前提下的(见定义1)。如果fs只考虑当前域,Decoder生成的结果就会偏离x,就会不满足约束条件。因此这个约束条件就把fs限制住了,让它对于所有域都具有不变性。
综上得知约束优化的含义:在保证fs对于所有域都具有不变性的前提下(约束条件),使fs在当前域有一个正确的输出标签(损失函数)。
那么问题又来了,如何训练Decoder保证向量充分解耦时才能得到正确的输出?(暂时还没看)
损失函数及训练过程
损失函数就是上面约束优化公式的变体,其中第一项是约束优化公式中的交叉熵损失,第二项就是约束条件,由于约束优化问题在边界取得最值,所以直接让d()-y逼近0即可满足约束条件。
(有个问题,xi和xj不一定是同一个域的啊)
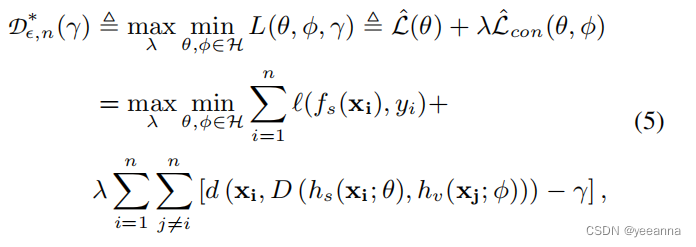

[27]表明,在某些条件下,即使是标准的经验风险最小化,也可能优于许多最近提出的模型。
以更小的计算量实现了更好的效果。
以下这些定理推论主要目的是推出公式(5)
1、基于解纠缠的不变性:x和x’分别是semantic和variation的输入,如果x和x’同分布,那么Generator的输出=x

2、基于解纠缠的域迁移:无论x与x’是否同分布,x输入semantic的分布与Generator输出的X经过semantic的分布是相同的