基于PCA对人脸识别数据降维并建立KNN模型检验
作者:i阿极
作者简介:Python领域新星作者、多项比赛获奖者:博主个人首页
😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏📁评论📒+关注哦!👍👍👍
📜📜📜如果有小伙伴需要数据集和学习交流,文章下方有交流学习区!一起学习进步!💪
大家好,我i阿极。喜欢本专栏的小伙伴,请多多支持
| 专栏案例:机器学习案例 |
|---|
| 机器学习(一):线性回归之最小二乘法 |
| 机器学习(二):线性回归之梯度下降法 |
| 机器学习(三):基于线性回归对波士顿房价预测 |
| 机器学习(四):基于KNN算法对鸢尾花类别进行分类预测 |
| 机器学习(五):基于KNN模型对高炉发电量进行回归预测分析 |
| 机器学习(六):基于高斯贝叶斯对面部皮肤进行预测分析 |
| 机器学习(七):基于多项式贝叶斯对蘑菇毒性分类预测分析 |
| 机器学习(十四):基于逻辑回归对超市销售活动预测分析 |
| 机器学习(十五):基于神经网络对用户评论情感分析预测 |
| 机器学习(十六):线性回归分析女性身高与体重之间的关系 |
| 机器学习(十七):基于支持向量机(SVM)进行人脸识别预测 |
| 机器学习(十八):基于逻辑回归对优惠券使用情况预测分析 |
| 机器学习(十九):基于逻辑回归对某银行客户违约预测分析 |
| 机器学习(二十):LightGBM算法原理(附案例实战) |
| 机器学习(二十一):基于朴素贝叶斯对花瓣花萼的宽度和长度分类预测 |
| 机器学习(二十二):基于逻辑回归(Logistic Regression)对股票客户流失预测分析 |
文章目录
- 基于PCA对人脸识别数据降维并建立KNN模型检验
- 1、PCA算法简介
- 2、数学原理
- 3、实验环境
- 4、实战案例-人脸识别
- 4.1案例背景
- 4.2数据读取
- 4.3数据处理
- 4.4数据划分与降维
- 4.5KNN模型的搭建与使用
1、PCA算法简介
PCA(Principal Component Analysis)是一种常用的数据降维方法,通过线性变换将高维数据映射到低维空间,同时尽量保留原始数据的信息。PCA的主要思想是将原始数据的各个特征进行线性组合,使得新特征能够最大程度地保留原始数据的方差,从而达到降维的目的。
PCA的具体步骤如下:
-
数据预处理:对数据进行标准化处理,使得每个特征的均值为0,方差为1。
-
计算协方差矩阵:将标准化后的数据按列组成n维列向量,计算其协方差矩阵。
-
计算特征值和特征向量:对协方差矩阵进行特征值分解,得到n个特征值和n个特征向量。
-
选择主成分:将特征值按大小排列,选择前k个特征值对应的特征向量,这些特征向量组成的矩阵即为转换矩阵。通常只选择特征值较大的几个特征向量,将高维数据映射到低维空间中,从而实现数据降维。
-
映射数据:将原始数据与转换矩阵相乘,得到新的低维数据。
PCA算法的主要优点是可以在不丢失太多信息的情况下降低数据的维度,从而减少计算量和存储空间。
2、数学原理
PCA(Principal Component Analysis)是一种线性降维技术,其数学原理涉及到线性代数中的特征值和特征向量。
给定一个数据矩阵 X ∈ R m × n X\in R^{m\times n} X∈Rm×n,其中 m m m表示样本数量, n n n表示特征数量。我们需要通过PCA将 X X X降维到 k k k维( k < n k<n k<n),得到一个新的数据矩阵 Z ∈ R m × k Z\in R^{m\times k} Z∈Rm×k,其中每一列代表着一个新的特征。
PCA的主要思想是将原始数据在新的坐标系中进行投影,使得投影后数据的方差最大。具体地,我们需要求出一个正交矩阵 W ∈ R n × k W\in R^{n\times k} W∈Rn×k,使得将原始数据 X X X乘以 W W W后得到的新数据矩阵 Z = X W Z=XW Z=XW,其中每一列都是正交的且具有最大方差。
因此,我们需要求解如下优化问题:
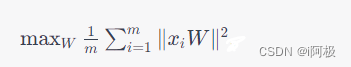
x i x_i xi表示数据矩阵 X X X的第 i i i行
为了求解上述问题,我们引入一个新的变量
U
=
X
W
U=XW
U=XW,该变量表示数据矩阵
X
X
X在新坐标系下的投影。由于
U
=
X
W
U=XW
U=XW,因此可以得到:
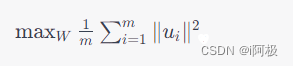
u i u_i ui表示 U U U的第 i i i行
为了让方差最大,我们需要将上述问题转化为一个约束最优化问题:
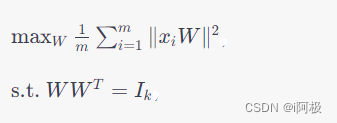
I k I_k Ik表示 k k k维单位矩阵
我们可以通过拉格朗日乘子法将上述问题转化为一个无约束问题:
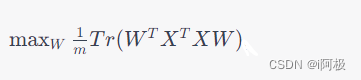
T r Tr Tr表示矩阵的迹
为了求解上述问题,我们需要求解矩阵 X T X X^TX XTX的特征值和特征向量,并选取前 k k k大的特征值所对应的特征向量组成一个新的矩阵 W W W。这个新的矩阵 W W W就是我们所需要的正交矩阵。
最后,我们将原始数据 X X X乘以矩阵 W W W,即可得到新的数据矩阵 Z = X W Z=XW Z=XW,其中每一列都代表着一个新的特征,且这些特征具有最大的方差。
3、实验环境
Python 3.9
Jupyter Notebook
Anaconda
4、实战案例-人脸识别
4.1案例背景
人脸识别是基于人的脸部特征信息进行身份识别的一种生物识别技术。该技术蓬勃发展,应用广泛,例如:人脸识别门禁系统,刷脸支付软件,公安人脸识别系统。这一节我们便以一个人脸识别模型来讲解如何在实战中应用PCA主成分分析算法。
该节所讲的人脸识别的本质其实是根据每张人脸不同像素点的颜色不同来进行数据建模与判断,人脸的每个像素点的颜色都有不同的值,这些值可以组成人脸的特征向量们,不过因为人脸上的像素点过多,所以特征变量过多,因此需要利用PCA进行主成分分析进行数据降维。
4.2数据读取
读取数据
import os
names = os.listdir("D:\\CSDN\\machine learning\\data\\faces")
names[0:5] # 查看前5项读取的文件名
获取到文件名称后,便可以通过如下代码在Python中查看这些图片
from PIL import Image
img0 = Image.open("D:\\CSDN\\machine learning\\data\\faces\\" + names[0])
img0.show()
img0

4.3数据处理
图像灰度处理及数值化处理
import numpy as np
img0 = img0.convert('L')
img0 = img0.resize((32, 32))
arr = np.array(img0)
arr # 查看数值化后的结果

为了方便数据建模,将二维数组转化为一维数组
arr = arr.reshape(1, -1)
print(arr)
构造所有图片的特征变量
X = [] # 特征变量
for i in names:
img = Image.open("D:\\CSDN\\machine learning\\data\\faces\\" + i)
img = img.convert('L')
img = img.resize((32, 32))
arr = np.array(img)
X.append(arr.reshape(1, -1).flatten().tolist())
查看400张图片转换后的结果
import pandas as pd
X = pd.DataFrame(X)
X
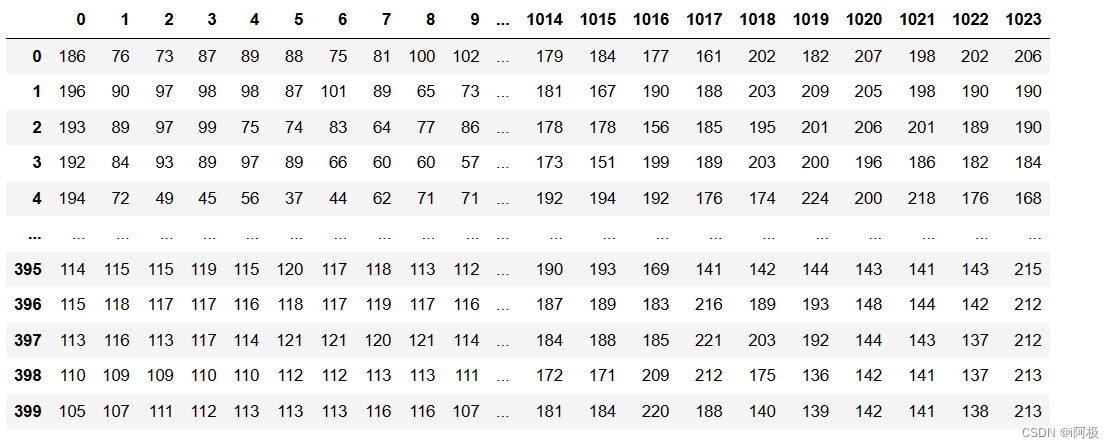
查看此时的表格结构
print(X.shape)
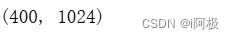
批量获取所有图片的目标变量y
y = [] # 目标变量
for i in names:
img = Image.open("D:\\CSDN\\machine learning\\data\\faces\\" + i)
y.append(int(i.split('_')[0]))
print(y) # 查看目标变量,也就是对应的人员编号

4.4数据划分与降维
划分训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
PCA数据降维
from sklearn.decomposition import PCA
pca = PCA(n_components=100)
pca.fit(X_train)
对训练集和测试集进行数据降维
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
验证PCA是否降维
print(X_train_pca.shape)
print(X_test_pca.shape)

4.5KNN模型的搭建与使用
模型搭建
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier() # 建立KNN模型
knn.fit(X_train_pca, y_train) # 用降维后的训练集进行训练模型
模型预测
y_pred = knn.predict(X_test_pca) # 用降维后的测试集进行测试
print(y_pred) # 将对测试集的预测结果打印出来

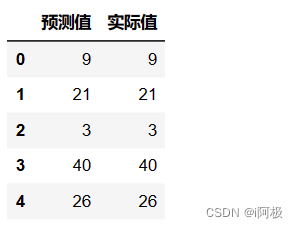
将预测值和实际值进行对比
import pandas as pd
a = pd.DataFrame() # 创建一个空DataFrame
a['预测值'] = list(y_pred)
a['实际值'] = list(y_test)
a.head() # 查看表格前5行
查看预测准确度
from sklearn.metrics import accuracy_score
score = accuracy_score(y_pred, y_test)
print(score)

📢文章下方有交流学习区!一起学习进步!💪💪💪
📢首发CSDN博客,创作不易,如果觉得文章不错,可以点赞👍收藏📁评论📒
📢你的支持和鼓励是我创作的动力❗❗❗





![博客系统[Java]](https://img-blog.csdnimg.cn/27ee73fa76c64a0faa8b89f152654113.png)


![C++——类和对象[上]](https://img-blog.csdnimg.cn/img_convert/72e265b270c8b0f3f4349794a11d16a6.png)