BFS算法专题
- 框架篇
- LeetCode 111. 二叉树的最小深度
- 解题思路
- 代码实现
- LeetCode 752. 打开转盘锁
- 解题思路
- 代码实现
- LeetCode 773. 滑动谜题
- 解题思路
- 代码实现
- 总结
不要纠结,干就完事了,熟练度很重要!!!多练习,多总结!!!
框架篇
BFS 问题的本质就是让你在一幅「图」中找到从起点start到终点target的最近距离,这个例子听起来很枯燥,但是 BFS 算法问题其实都是在干这个事儿。
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
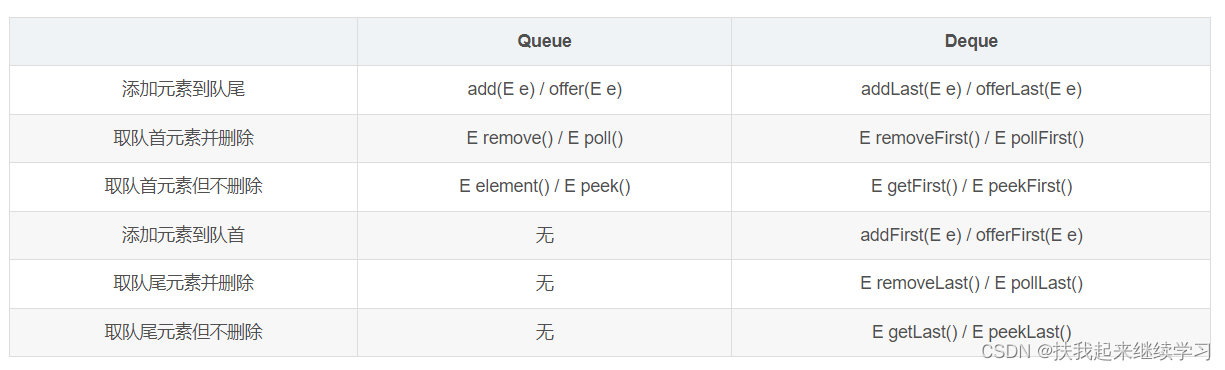
Queue<Node> q; // 核心数据结构
Set<Node> visited; // 避免走回头路
q.offer(start); // 将起点加入队列
visited.add(start);
int step = 0; // 记录扩散的步数
while (q not empty) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
/* 划重点:这里判断是否到达终点 */
if (cur is target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj())
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
/* 划重点:更新步数在这里 */
step++;
}
}
队列q就不说了,BFS 的核心数据结构;cur.adj()泛指cur相邻的节点,比如说二维数组中,cur上下左右四面的位置就是相邻节点;visited的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有子节点到父节点的指针,不会走回头路就不需要visited。
- 为什么 BFS 可以找到最短距离,DFS 不行吗?
首先,你看 BFS 的逻辑,depth每增加一次,队列中的所有节点都向前迈一步,这保证了第一次到达终点的时候,走的步数是最少的。
DFS 不能找最短路径吗?其实也是可以的,但是时间复杂度相对高很多。
DFS 实际上是靠递归的堆栈记录走过的路径,你要找到最短路径,肯定得把二叉树中所有树杈都探索完才能对比出最短的路径有多长对不对?
BFS 借助队列做到一次一步「齐头并进」,是可以在不遍历完整棵树的条件下找到最短距离的。
形象点说,DFS 是线,BFS 是面;DFS 是单打独斗,BFS 是集体行动。这个应该比较容易理解吧。
- 既然 BFS 那么好,为啥 DFS 还要存在?
BFS 可以找到最短距离,但是空间复杂度高,而 DFS 的空间复杂度较低。
拿《LeetCode 111. 二叉树的最小深度》举例,假设给你的这个二叉树是满二叉树,节点总数为N,对于 DFS 算法来说,空间复杂度无非就是递归堆栈,最坏情况下顶多就是树的高度,也就是O(logN)。
BFS 算法,队列中每次都会储存着二叉树一层的节点,这样的话最坏情况下空间复杂度应该是树的最底层节点的数量,也就是N/2,用 Big O 表示的话也就是O(N)。
BFS 还是有代价的,一般来说在找最短路径的时候使用 BFS,其他时候还是 DFS 使用得多一些(主要是递归代码好写)。
LeetCode 111. 二叉树的最小深度

解题思路
题目要求求出最小高度,BFS通过队列可以做到从根节点往下“齐头并进”进行逐行扫描,那么终止条件是什么呢?走到叶子结点即该节点的左右子树均为空,便可以返回。
代码实现
class Solution {
public int minDepth(TreeNode root) {
if(root == null){
return 0;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
int dep = 1;
while(!queue.isEmpty()){
int size = queue.size();
for(int i = 0; i < size;i++){
TreeNode cur = queue.poll();
if(cur.left == null && cur.right == null){
return dep;
}
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
}
dep++;
}
return dep;
}
}
LeetCode 752. 打开转盘锁

解题思路
我们不管所有的限制条件,不管deadends和target的限制,就思考一个问题:如果让你设计一个算法,穷举所有可能的密码组合,你怎么做?
// 将 s[j] 向上拨动一次
String plusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '9')
ch[j] = '0';
else
ch[j] += 1;
return new String(ch);
}
// 将 s[i] 向下拨动一次
String minusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '0')
ch[j] = '9';
else
ch[j] -= 1;
return new String(ch);
}
// BFS 框架,打印出所有可能的密码
void BFS(String target) {
Queue<String> q = new LinkedList<>();
q.offer("0000");
while (!q.isEmpty()) {
int sz = q.size();
/* 将当前队列中的所有节点向周围扩散 */
for (int i = 0; i < sz; i++) {
String cur = q.poll();
/* 判断是否到达终点 */
System.out.println(cur);
/* 将一个节点的相邻节点加入队列 */
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
String down = minusOne(cur, j);
q.offer(up);
q.offer(down);
}
}
/* 在这里增加步数 */
}
return;
}
这段 BFS 代码已经能够穷举所有可能的密码组合了,但是显然不能完成题目,有如下问题需要解决:
- 会走回头路。比如说我们从"0000"拨到"1000",但是等从队列拿出"1000"时,还会拨出一个"0000",这样的话会产生死循环。
- 没有终止条件,按照题目要求,我们找到target就应该结束并返回拨动的次数。
- 没有对deadends的处理,按道理这些「死亡密码」是不能出现的,也就是说你遇到这些密码的时候需要跳过。
代码实现
class Solution {
public int openLock(String[] deadends, String target) {
Set<String> dead = new HashSet<>();
for(String s:deadends){
dead.add(s);
}
Set<String> visit = new HashSet<>();
Queue<String> queue = new LinkedList<>();
queue.offer("0000");
visit.add("0000");
int step = 0;
while(!queue.isEmpty()){
int size = queue.size();
for(int i = 0;i < size;i++){
String cur = queue.poll();
if(dead.contains(cur)){
continue;
}
if(cur.equals(target)){
return step;
}
for(int j=0;j < 4;j++){
String up = plusOne(cur, j);
if(!visit.contains(up)){
queue.offer(up);
visit.add(up);
}
String down = deOne(cur, j);
if(!visit.contains(down)){
queue.offer(down);
visit.add(down);
}
}
}
step++;
}
return -1;
}
public String plusOne(String cur, int i){
char[] ch = cur.toCharArray();
if(ch[i] == '9'){
ch[i] = '0';
}else{
ch[i]+=1;
}
return new String(ch);
}
public String deOne(String cur, int i){
char[] ch = cur.toCharArray();
if(ch[i] == '0'){
ch[i] = '9';
}else{
ch[i]-=1;
}
return new String(ch);
}
}
LeetCode 773. 滑动谜题
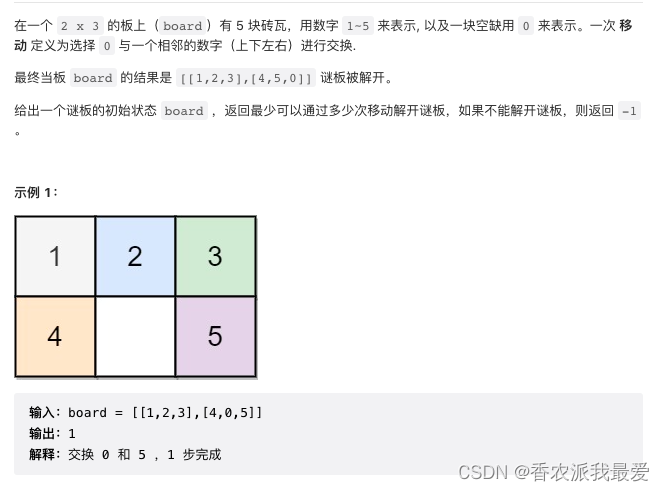
解题思路
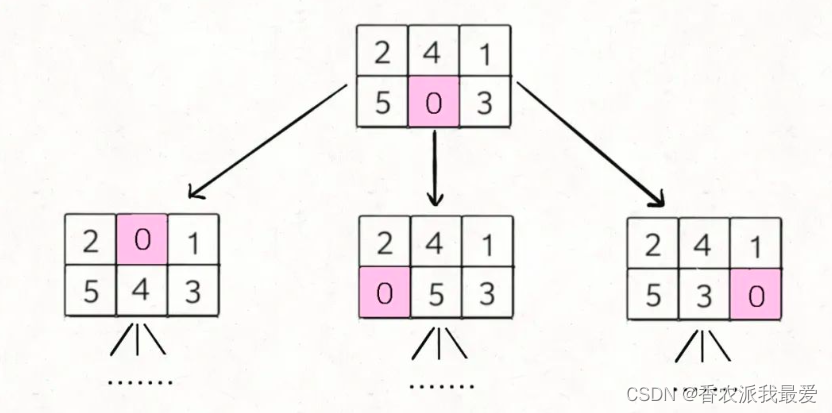
其中比较有技巧性的点在于,二维数组有「上下左右」的概念,压缩成一维后,如何得到某一个索引上下左右的索引?
vector<vector<int>> neighbor = {
{ 1, 3 },
{ 0, 4, 2 },
{ 1, 5 },
{ 0, 4 },
{ 3, 1, 5 },
{ 4, 2 }
};
这个含义就是,在一维字符串中,索引i在二维数组中的的相邻索引为neighbor[i]
代码实现
class Solution {
int[][] neighbors = {{1, 3}, {0, 2, 4}, {1, 5}, {0, 4}, {1, 3, 5}, {2, 4}};
public int slidingPuzzle(int[][] board) {
Queue<String> queue = new LinkedList<>();
Set<String> visit = new HashSet<>();
int step = 0;
StringBuilder sb = new StringBuilder();
for(int i = 0;i < 2;i++){
for(int j = 0;j < 3;j++){
sb.append(board[i][j]);
}
}
queue.offer(sb.toString());
visit.add(sb.toString());
String target = "123450";
while(!queue.isEmpty()){
int size = queue.size();
for(int i = 0; i < size;i++){
String cur = queue.poll();
if(cur.equals(target)){
return step;
}
int idx = cur.indexOf('0');
for(int adj : neighbors[idx]){
String ready = cur;
String swapStr = swap(ready, idx, adj);
if(!visit.contains(swapStr)){
queue.offer(swapStr);
visit.add(swapStr);
}
}
}
step++;
}
return -1;
}
public String swap(String cur, int i, int j){
char[] ch = cur.toCharArray();
char tmp = ch[i];
ch[i] = ch[j];
ch[j] = tmp;
return new String(ch);
}
}
总结
本题来源于Leetcode中 归属于BFS算法类型题目。
同许多在算法道路上不断前行的人一样,不断练习,修炼自己!
如有博客中存在的疑问或者建议,可以在下方留言一起交流,感谢各位!
觉得本博客有用的客官,可以给个点赞+收藏哦! 嘿嘿
喜欢本系列博客的可以关注下,以后除了会继续更新面试手撕代码文章外,还会出其他系列的文章!