本文只是对学习过程中的点云密度降采样的几种方法做一个记录,原文参考知乎Python点云数据处理(四)点云下采样 - 知乎 (zhihu.com)
本文介绍python点云数据处理中的点云下采样算法和关键点算法以及在点云工具箱软件中的实现。由于点云的海量和无序性,直接处理的方式在对邻域进行搜索时需要较高的计算成本。一个常用的解决方式就是对点云进行下采样,将对全部点云的操作转换到下采样所得到的点上,降低计算量。
一、均匀下采样
均匀下采样有多种不同的采样方式,其中最远点采样是较为简单的一种,首先需要选取一个种子点,并设置一个内点集合,每次从点云中不属于内点的集合找出一点距离内点最远的点,如下图,这里的距离计算方式为该点至内点所有点的最小距离。这种方式的下采样点云分布均匀,但是算法复杂度较高效率低。
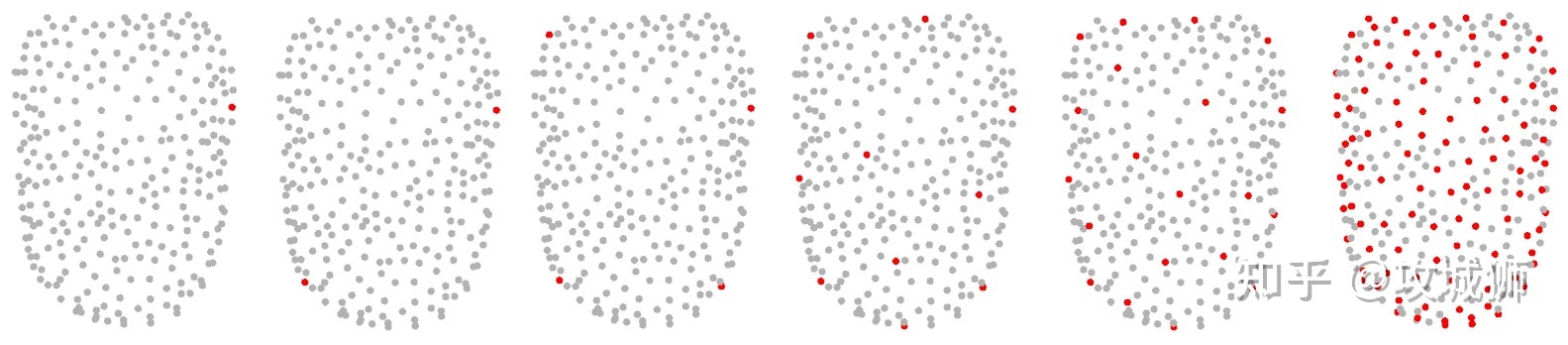
点云工具箱中该功能实现依赖于Open3d库,代码如下:
import open3d as o3d
# 读取文件
pcd = o3d.io.read_point_cloud(path) # path为文件路径
pcd_new = o3d.geometry.PointCloud.uniform_down_sample(pcd, value)
# value值的设定为整数,即value个点中选取一个点二、体素下采样
体素下采样就是把三维空间体素化,然后在每个体素里采样一个点,通常可用中心点或最靠近中心的点作为采样点。具体方法如下:
1. 创建体素:计算点云的包围盒,然后把包围盒离散成小体素。体素的长宽高可以用户设定,也可以通过设定包围盒三个方向的格点数来求得。
2. 每个小体素包含了若干个点,取中心点或离中心点最近的点为采样点。
体素采样的特点:
- 效率非常高
- 采样点分布比较均匀,但是均匀性没有均匀采样高
- 可以通过体素的尺寸控制点间距
- 不能精确控制采样点个数
点云工具箱中该功能实现依赖于Open3d库,代码如下:
pcd_new = o3d.geometry.PointCloud.voxel_down_sample(pcd, value)
# value为体素的大小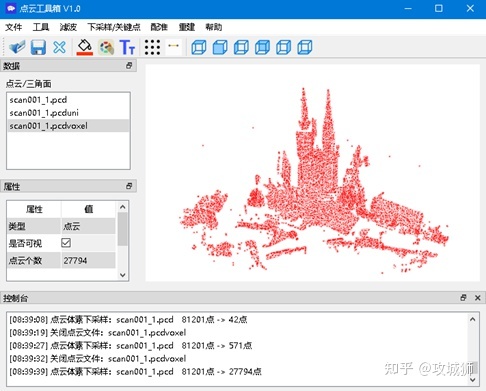
三、曲率下采样
曲率下采样就是在点云曲率越大的地方,采样点个数越多。一种简单有效的曲率下采样实现方法如下:
1.通过该方法近似达到曲率的效果同时提高计算效率:计算每个点K邻域,然后计算点到邻域点的法线夹角值。曲率越大的地方,这个夹角值就越大。
2.设置一个角度阈值,比如5度。点的邻域夹角值大于这个阈值的点被认为是特征明显的区域,其余的为不明显区域。
3.均匀采样特征明显区域和不明显区域,采样数分别为S * (1 - U),S * U。S为目标采样数,U为采样均匀性。
该采样方法的特点:
- 几何特征越明显的区域,采样点个数分布越多
- 计算效率高
- 采样点局部分布是均匀的
- 稳定性高:通过几何特征区域的划分,使得采样结果抗噪性更强
点云工具箱中该功能实现代码如下:
def vector_angle(x, y):
Lx = np.sqrt(x.dot(x))
Ly = (np.sum(y ** 2, axis=1)) ** (0.5)
cos_angle = np.sum(x * y, axis=1) / (Lx * Ly)
angle = np.arccos(cos_angle)
angle2 = angle * 360 / 2 / np.pi
return angle2
knn_num = 10 # 自定义参数值(邻域点数)
angle_thre = 30 # 自定义参数值(角度值)
N = 5 # 自定义参数值(每N个点采样一次)
C = 10 # 自定义参数值(采样均匀性>N)
pcd = o3d.io.read_point_cloud(path)
point = np.asarray(pcd.points)
point_size = point.shape[0]
tree = o3d.geometry.KDTreeFlann(pcd)
o3d.geometry.PointCloud.estimate_normals(
pcd, search_param=o3d.geometry.KDTreeSearchParamKNN(knn=knn_num))
normal = np.asarray(pcd.normals)
normal_angle = np.zeros((point_size))
for i in range(point_size):
[_, idx, dis] = tree.search_knn_vector_3d(point[i], knn_num + 1)
current_normal = normal[i]
knn_normal = normal[idx[1:]]
normal_angle[i] = np.mean(vector_angle(current_normal, knn_normal))
point_high = point[np.where(normal_angle >= angle_thre)]
point_low = point[np.where(normal_angle < angle_thre)]
pcd_high = o3d.geometry.PointCloud()
pcd_high.points = o3d.utility.Vector3dVector(point_high)
pcd_low = o3d.geometry.PointCloud()
pcd_low.points = o3d.utility.Vector3dVector(point_low)
pcd_high_down = o3d.geometry.PointCloud.uniform_down_sample(pcd_high, N)
pcd_low_down = o3d.geometry.PointCloud.uniform_down_sample(pcd_low, C)
pcd_finl = o3d.geometry.PointCloud()
pcd_finl.points = o3d.utility.Vector3dVector(np.concatenate((np.asarray(pcd_high_down.points),
np.asarray(pcd_low_down.points))))四、曲面均匀采样
曲面均匀采样的算法实现依赖于Open3d库,从三角网格曲面数据均匀采样得到点云。

点云工具箱中该功能实现依赖于Open3d库,代码如下:
ply = o3d.io.read_triangle_mesh(path)
pcd = ply.sample_points_uniformly(number_of_points = value) # number_of_points参数为采样点数五、泊松磁盘采样
1. 泊松磁盘采样(Poisson-Disk Sampling)性质
一个理想的 Poisson 圆盘采样点集需要满足 3 个条件:
(1) 无偏差采样性质 (采样区域的每个没有被覆盖的点都有相同的概率接受一个新的采样点);
(2) 最小距离性质 (任意两个采样点之间的距离大于给定的采样半径);
(3) 最大化性质 (采样区域被所有的采样圆盘完全覆盖).
满足这 3 个条件的采样方法称为最大化 Poisson 圆盘采样 (maximal Poisson-disk sampling, MPS).
2.Poisson-Disk Sampling伪代码如下:
function WeightedSamplingElim(samples)
Build a K-Dtree for each samples
Assign weights wi to each sample si
Build a heap for si using weights wi
While number of samples > desired
sj <- pull the top sample from heap
For each sample si around sj
Remove wij from wi
Update the heap position of si每个sample都会被分配一个对应的权重,其权重的参数如下:
w[index] += weightFunction(point, p, d2, d_max)
其中point为每个泊松圆盘固定点,p为point周围的点,d2为周围点与point之间的距离
,d_max为设定Poisson radius距离。
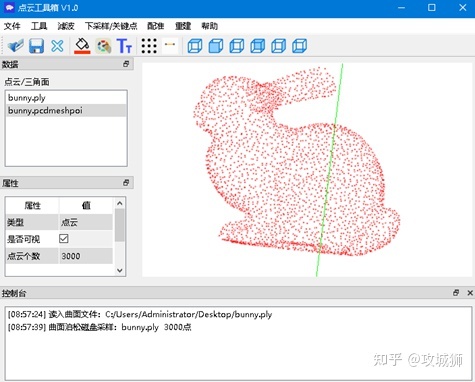
点云工具箱中该功能实现依赖于Open3d库,代码如下:
pcd = tri_mesh.sample_points_poisson_disk(number_of_points=value) # number_of_points参数为采样点数