目录
1 测量学基础
1.1 地球的形状和大小
1.1.1 大地水准面
1.1.2 大地体
1.1.3 地球椭球
2 坐标系统
2.1 地理坐标系
2.2 投影坐标系
2.3 局部坐标系(假定坐标系)
2.4 高程坐标系
3 地图投影
3.1 投影概念
3.2 投影分类
3.3 投影类型
3.4 投影面与地球表面关系
4 常见投影地图
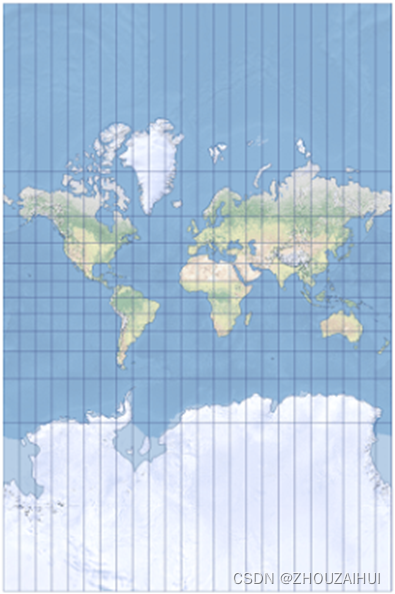
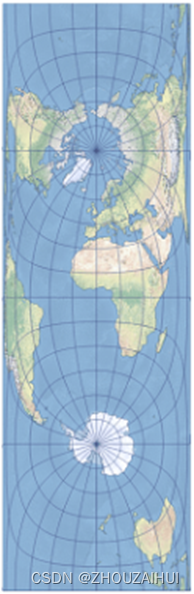
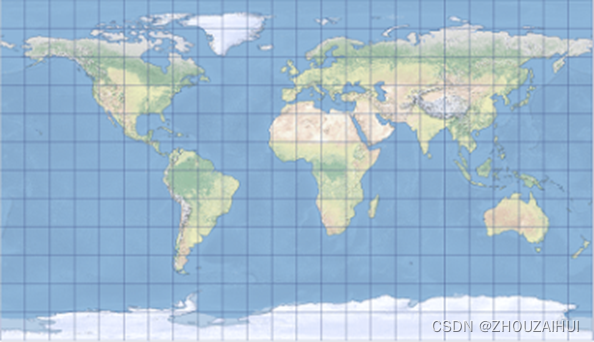
4.1 世界地图
4.1.1 中国版世界地图
4.1.2 欧洲版世界地图
4.1.3 俄罗斯版世界地图
4.1.4 澳大利亚版世界地图
4.1.5 美国版世界地图
4.1.6 巴西版世界地图
4.1.7 南极版世界地图
4.2 各种投影地图
4.2.1 柏哥斯星状投影
4.2.2 彭纳 (Bonne) 投影
4.2.3 等距方位 (Azimuthal equidistant) 投影
4.2.4 立方体投影
4.2.5 富勒 (Fuller) 投影
4.2.6 温克尔三重 (Winkel Tripel) 投影
4.2.7 古蒂(Goode)等积投影
4.2.8 埃托夫 (Aitoff) 投影
4.2.9 正射 (Orthographic) 投影
4.2.10 墨卡托投影(Mercator)
4.2.11 微信登录界面
5 国内常见投影系统
5.1 高斯-克吕格(Gauss-Krüger)投影-等角投影
5.2 通用横轴墨卡托(UTM)投影
5.3 兰伯特(Lambert)投影-等角投影
5.4 阿尔伯斯(Albers)投影-等积投影
5. 5 WEB墨卡托(Web Mercator)投影
6 国内常用坐标系统
6.1 北京54坐标系统(BJZ54)
6.2 西安80坐标系统(Xian80)
6.3 2000国家大地坐标系统(CGCS2000)
6.4 1956黄海高程基准
6.5 1985国家高程基准
6.6 WGS84坐标系统
6.7 GCJ-02坐标系统(高德地图、腾讯地图等)
6.8 BD-09坐标系统(百度地图)
7 投影(平面)坐标系统(以高斯投影为例)
7.1 投影类型
7.2 我国常用的投影方式
7.2.1 全国投影参数
7.2.2 中国分省投影参数
7.3 投影分带
7.4 投影坐标定义
7.4.1 高斯-克吕格(Gauss-Kruger)投影平面坐标
7.4.2 独立平面直角坐标
7.4.3 高斯平面直角坐标(测量坐标)与笛卡尔坐标(几何坐标)异同
8 ArcGIS Pro中的坐标系统
8.1 国际上定义坐标系统的主要组织
8.1.1 ESPG
8.1.2 OGC
8.1.3 ESRI
8.1.4 结论
8.2 高斯-克吕格投影
8.3 Lambert等角投影
8.4 Albers等积投影
8.5 UTM投影
8.6 WEB墨卡托投影
GIS中会用到大量的图形数据,而图形数据一般会带有一定的坐标信息,坐标信息承载的是图形数据的基本地理位置,因此需要对坐标系统有深入的了解。而地图数据的获取一般最简单的方法是通过测量得到,因此测量学中所定义的坐标系统一般也会继承并延续到相关的GIS图形数据中。

1 测量学基础
1.1 地球的形状和大小
通常所说的测量工作一般是指在地球表面进行的,因此需要有一个作为标准的测量基准才能保证测量工作的准确性和延续性。这个测量基准一般会选取一个简单规则形状,而地球自然表面高低起伏不平,不能作为测量工作的基准。应该寻找一个与地球自然表面十分接进而且相对简单的规则曲面来代替不规则的地球表面。
1.1.1 大地水准面
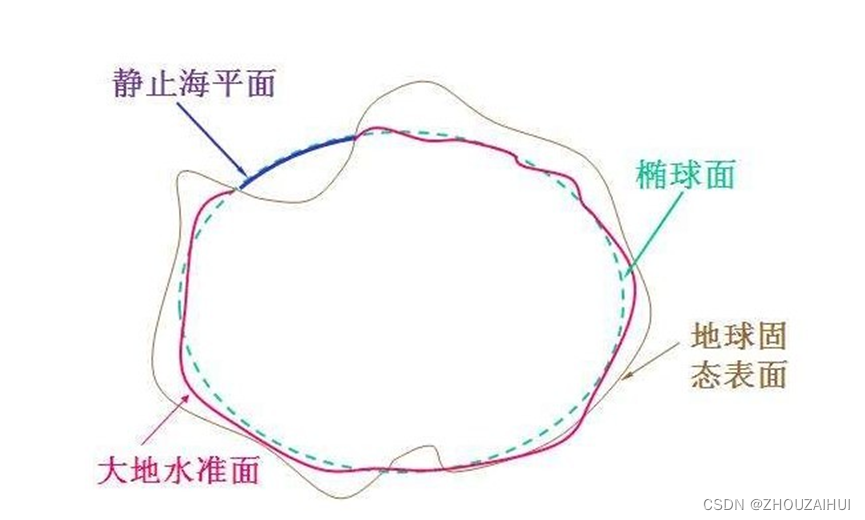
根据地球重力场的特性,可找到重力位处处相等的很多个等位面,可理解为水在静止状态下形成的曲面,测量学称之为水准面。测量学研究的是在整体上非常接进地球表面的水准面,是一个无波浪、无潮汐、无水流、无大气压变化,处于流体平衡状态的静止海平面。以这个海平面为基准面并向大陆岛屿延伸围合形成一个封闭曲面,即测量学中的大地水准面。
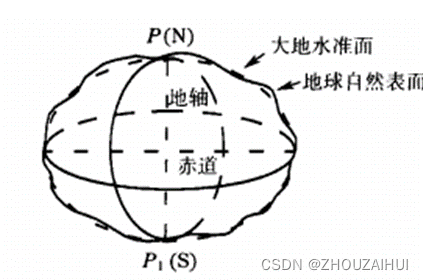


1.1.2 大地体
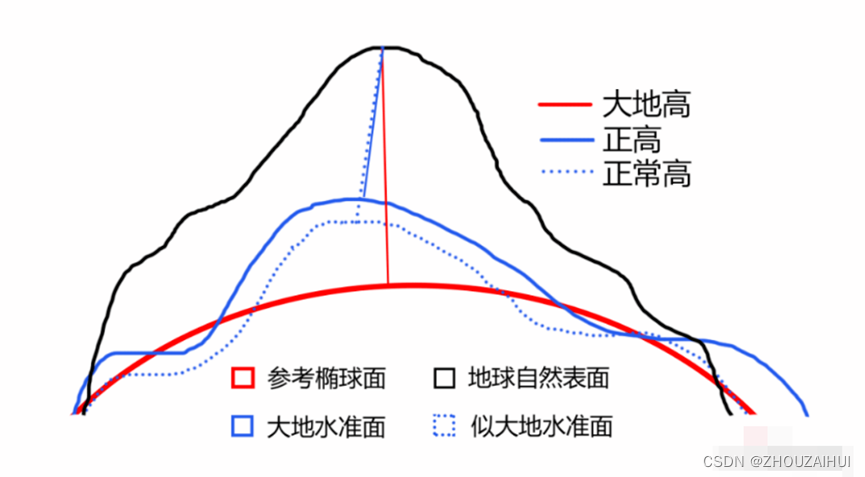
大地水准面的形状(几何特性)和重力场(物理特性)都是不规则的,还不能用一个简单的数学公式描述其形状,因此需要在大地水准面的基础上再次找到一个似大地水准面近似代替大地水准面。似大地水准面与大地水准面在海洋上完全重合,陆地上只在山区有2-4m的误差。
似大地水准面围合而成大地体,是地球形状的近似,它仍然是不规则曲面。
 .
.
1.1.3 地球椭球
大地体的表面仍然不能用数学模型精确定义和表述,必须寻找一个与大地体极其接近的形体来代替。如果将大地体绕短轴旋转一周就会形成一个表面光滑的旋转椭球,即地球椭球体。地球椭球体表面可以用数学模型定义和表述。

地球椭球几何参数包括:
椭球长半轴 a
椭球短半轴 b
椭球扁率
椭球第一偏心率
椭球第二偏心率
| 1940克拉索夫斯基椭球体 | 1975IUGG椭球体 | WGS84椭球体 | CGCS2000椭球体 | |
| 长半轴 | 6378245m | 6378140 | 6378137 | 6378137 |
| 短半轴 | 6356863.0187730473 | 6356755.288157528 | 6356752.3142451795 | 6356752.3141403558 |
| 扁率 | 1/298.3 | 1/298.257 | 1/298.2572235629972 | 1/298.2572221010042 |
| 第一偏心率 | 0.006693421622966 | 0.00669438499959 | 0. 0066493799013 | 0.00669438002290 |
| 第二偏心率 | 0.006738525414683 80 | 0.00673950181947 | 0. 00673949674227 | 0.00673949677548 |
地球椭球物理参数包括:
地心引力常数GM、正常化二阶带球谐系数C2.0、地球自转角速度ω等。
2 坐标系统
地球椭球就是测量工作研究的基准。所有的工作都需要从地球椭球面上进行研究,这与地球表面高低起伏的形态不相符,因此需要把地球表面的点按重力线方向投射到大地水准面上才能进行相关的研究。
因此地面点的位置表示的时候实际上是分成两部分:(1)大地水准面投射下来的点位置;(2)地面点沿重力方向线投射到大地水准面的铅垂距离。

2.1 地理坐标系
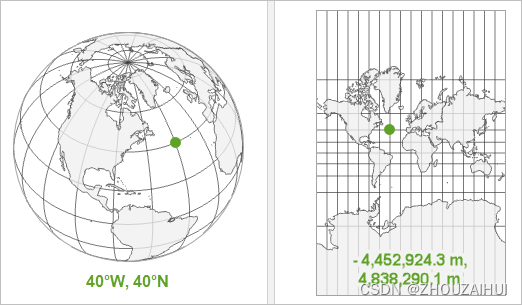
地理坐标系(Geographic Coordinate System,GCS)使用三维球面来定义地球上的位置。点要素可通过其经度和纬度值进行引用。经度和纬度是从地心到地球表面上某点的测量角。通常以度或百分度为单位来测量该角度的值。

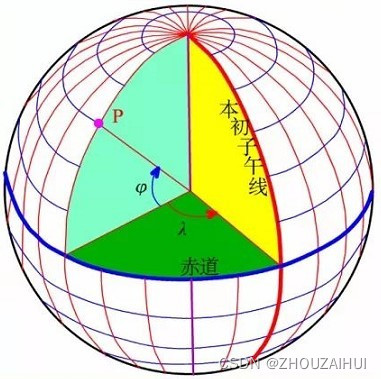

位于两极点中间位置的纬线称为赤道。它定义的是零纬度线。零经度线称为本初子午线。对于绝大多数地理坐标系,本初子午线是指通过英国格林尼治的经线。其他国家/地区使用通过伯尔尼、波哥大和巴黎的经线作为本初子午线。经纬网的原点 (0,0) 定义在赤道和本初子午线的交点处。这样,地球就被分成四个地理象限,它们均基于与原点所成的罗盘方位角。南和北分别位于赤道的下方和上方,而西和东分别位于本初子午线的左侧和右侧。

通常经度和纬度值以十进制度为单位或以度、分和秒 (DMS) 为单位进行测量。纬度值相对于赤道进行测量,其范围是 -90°(南极点)到 +90°(北极点)。经度值相对于本初子午线进行测量。其范围是 -180°(向西行进时)到 180°(向东行进时)。如果本初子午线是格林尼治子午线,则对于位于赤道南部和格林尼治东部的澳大利亚,其经度为正值,纬度为负值。
用 X 表示经度值并用 Y 表示纬度值。尽管经度和纬度可定位地球表面的准确位置,但它们不是均匀的测量单位。只有在赤道上,一经度所表示的距离才约等于一纬度所表示的距离。这是因为赤道是唯一与经线等长的纬线。
高程值Z通常采用地面点到大地水准面的铅垂距离(大地高)来表示。
因此地理坐标系的坐标表现形式为(X(经度),Y(纬度),Z(大地高))
2.2 投影坐标系
投影坐标系(Projection Coordinate System, PCS)是二维平面坐标。与地理坐标系不同,在二维空间范围内,投影坐标系的长度、角度和面积恒定。投影坐标系始终基于地理坐标系,而地理坐标则基于球体或椭圆体。
在投影坐标系中,通过格网上的 x,y 坐标来标识位置,其原点位于格网中心。每个位置均具有两个值,这两个值是相对于该中心位置的坐标。一个指定其水平位置,另一个指定其垂直位置。这两个值分别称为 x 坐标和 y 坐标。采用此标记法,原点的坐标值是 x = 0 和 y = 0。
在等间隔水平线和垂直线的格网化网络中,中央水平线称为 x 轴,而中央垂直线称为 y 轴。在 x 和 y 的整个范围内,单位保持不变且间隔相等。原点上方的水平线和原点右侧的垂直线具有正值;下方或左侧的线具有负值。四个象限分别表示正负 X 坐标和 Y 坐标的四种可能组合。

2.3 局部坐标系(假定坐标系)
局部坐标系通常用于小区域范围内的大比例尺地形图表达。坐标原点(0,0)可以与已知的实际坐标对齐,也可以选在区域西南角使得XY坐标为正值,可能使用局部坐标系而非全球坐标测量方位角和距离。通常以英尺或米表示局部坐标系(平面坐标)。
2.4 高程坐标系

绿色线代表大地水准面。曲线大致遵循地形的走向。虚线代表椭圆体的表面。h 是高出椭球体或椭圆体的高度 (HAE)。在本例中,高度是负值。N 代表大地水准面波动,它是椭圆体表面与大地水准面之间的距离。H 代表正高,它与椭圆体高度的关系:h = H + N
高程坐标系可以定义高度或深度值的原点。与水平坐标系类似,除非要显示数据集或者要将数据集与使用不同高程坐标系的其他数据合并,否则高程坐标系中的大部分信息都不需要使用。
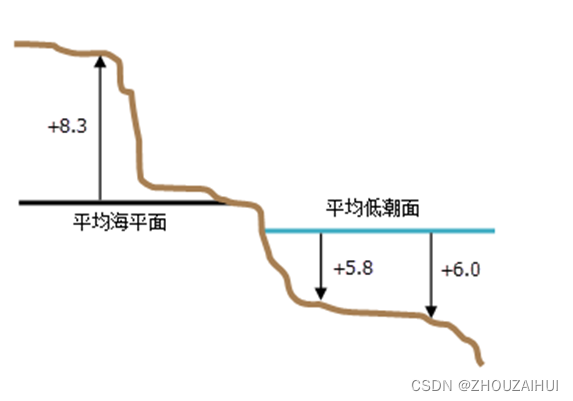
测量单位可能是高程坐标系最重要的部分。测量单位始终是线性的(例如,国际英尺或米)。另一个重要部分是 z 值究竟代表高度(高程)还是深度。对于每种类型,z 轴方向分别为正“北”或正“南”。下图显示了两个垂直坐标系:平均海平面和平均低潮面。平均海平面用作高度值的零水平面。平均低潮面则是基于深度的垂直坐标系。
3 地图投影
3.1 投影概念



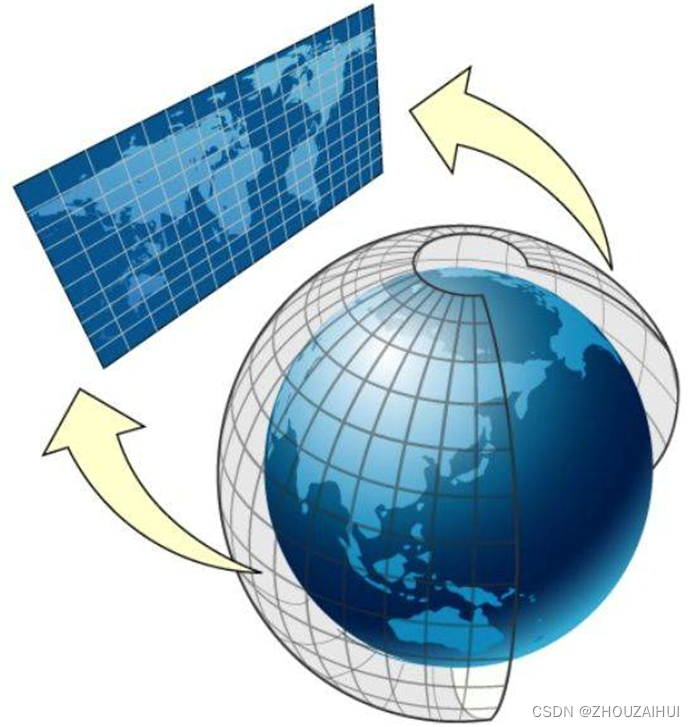
投影数学上的含义是两个面(平面或曲面)上点与点或线与线之间的一一对应关系,在一个面上的点(线),在另一个面上只有唯一的点(线)与之对应。
3.2 投影分类
地图投影的变形不可避免,通常可以分为长度、面积和角度三种。
(1)等角投影
等角投影保持局部形状不变。要保留描述空间关系的所有角度,等角投影必须在地图上显示以 90 度角相交的垂直经纬线。地图投影通过保持所有角度不变来加以实现。
缺点是由一些弧线围起来的区域将在此过程中发生巨大变形。地图投影无法保留较大区域的形状。
(2)等积投影
等积投影保持所显示要素的面积不变。形状、角和比例等其他属性都将发生变形。在等积投影中,经线和纬线可能不垂直相交。
缺点是有些情况下,尤其是较小区域的地图,形状不会明显变形,且很难区分等积投影和等角投影,除非加以说明或进行测量。
(3) 等距投影
等距地图保持某些点间的距离不变。任何投影都无法在整幅地图中正确保持比例不变。多数情况下,地图上总会存在一条或多条比例值会得以正确地保留的线。多数等距投影都具有一条或多条地图上线的长度(按地图比例计算)与地球上同一条线的长度相同的线:在此类线中,无论它是大圆还是小圆,是直线还是曲线。此类距离被视为真实距离。
(4) 等方位投影
曲面上两点间的最短路径是沿平面上直线的球面等价线。即两点所在的大圆。真方向(或方位)投影维持某些大圆圆弧不变,从而能够相对于中心正确地给出地图上所有点的方向或方位角。

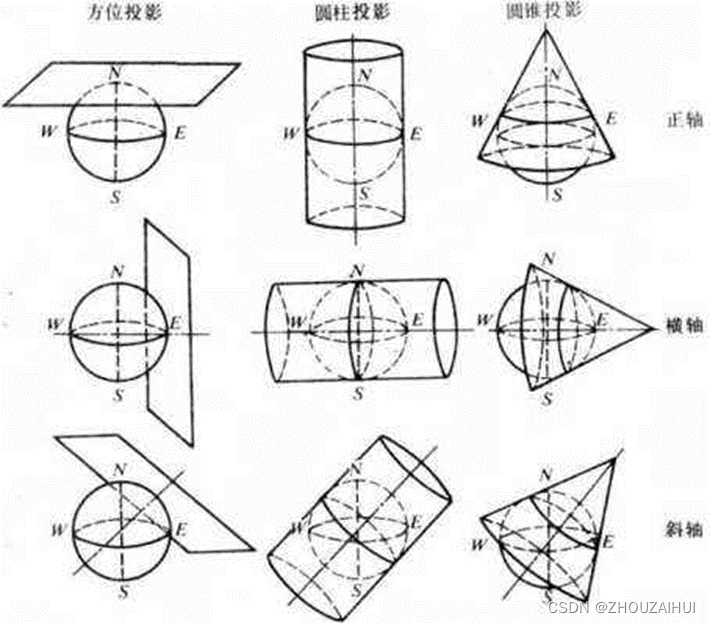
3.3 投影类型
由于地图是平的,因此一些最简单的投影就是投影到几何形状上,该形状可被展平,而不会拉伸其曲面。这些曲面被称为可展开曲面。圆锥曲面、圆柱曲面和平面即为一些常用的可展开曲面。地图投影使用数学算法系统地对位置进行投影,从旋转椭球体的曲面投影到平面上的对应位置。

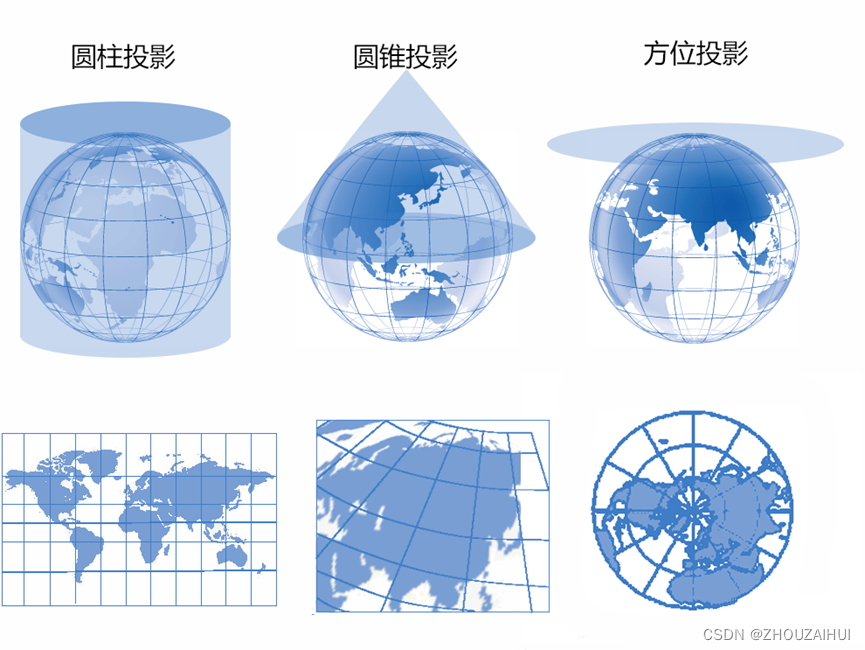
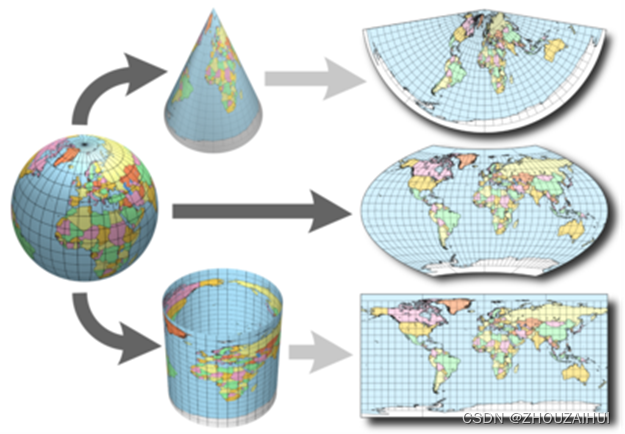
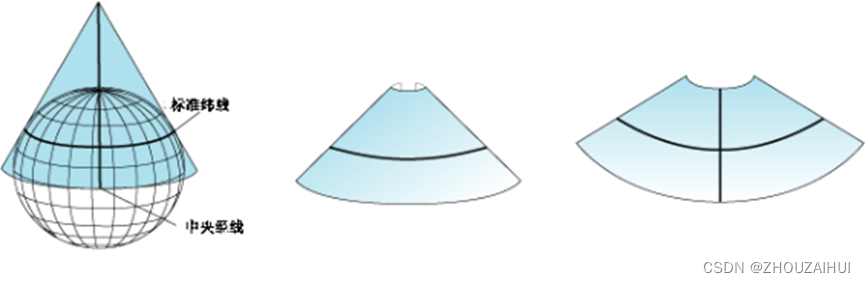
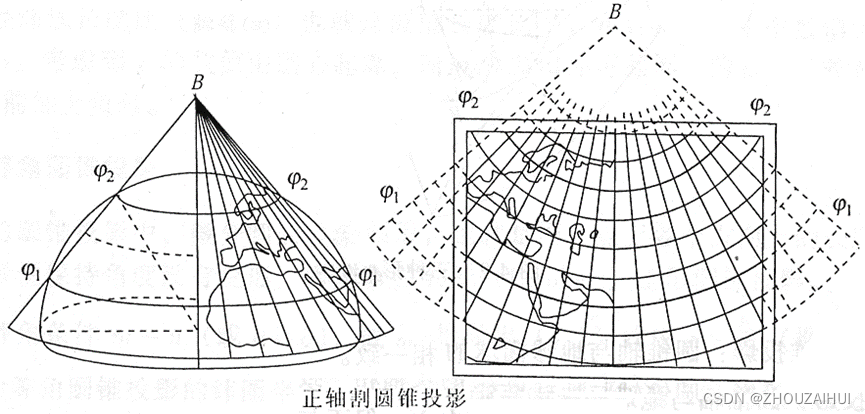
(1) 圆锥投影
最简单的圆锥投影是沿一条纬线与地球相切获得的投影。这条纬线称作标准纬线。所有的经线都投影到圆锥面上,并在圆锥的折点或某一点处相交。纬线在圆锥面上的投影是一个个环。将圆锥沿任意一条经线“剪开”后即可获得最终的圆锥投影,投影中的经线显示为汇聚到一点的直线,而纬线显示为许多的同心圆弧。与剪开线相对的经线成为中央经线。
圆锥被置于地球上。圆锥和地球沿一条纬线相交。该纬线就是标准纬线。沿中央子午线对面的经线切开圆锥,并将其展平为平面。
(2)圆柱投影
圆柱投影也存在相切或相割两种情况。墨卡托投影是最常用的圆柱投影之一,并且通常以赤道为切线。经线以几何方式投影到圆柱面上,而纬线以数学方式进行投影。这种投影方式产生成90度的经纬网格。将圆柱沿任意一条经线“剪开”可以获得最终的圆柱投影。经线等间距排列,而纬线间的间距越靠近极点越大。此投影是等角投影,并沿直线显示真实的方向。在墨卡托投影中,等角航线、等方位线是直线,但大多数的大圆都不是直线。

圆柱被置于地球上。圆柱可沿一条纬线(正常情况)、一条经线(横轴情况)或其他线(斜轴情况)接触地球。
(3) 方位投影(平面投影)
平面投影将地图数据投影到与地球接触的平面。平面投影也称为方位投影或天顶投影。
此类型的投影通常在一点与地球相切,但也可能相割。接触点可以是北极、南极、赤道上的某点或者赤道与两极之间的任意点。此点会指定投影方向,并作为投影的焦点。焦点由中央经度和中央纬度标识。可能的投影方法包括极方位投影、赤道投影和斜轴投影。
极方位投影是最简单的形式。纬线是以极点为中心的同心圆,经线是在极点处与其真实的方向角相交的直线。在其他投影方法中,平面投影在焦点处具有90度的经纬网。由焦点确定的方向是精确的。 
平面被置于地球上。平面可在极点(两极情况)、赤道(赤道情况)或其他线(倾斜情况)处接触地球。

方位投影或平面投影可具有不同的透视点。球心投影的透视点位于地球的中心。与接触点相对的地球另一侧用来进行立体投影。正射投影的透视点位于无限远处。
3.4 投影面与地球表面关系
(1)正轴投影:极点在两地极上,或投影面的中心线与地轴一致。
(2)斜轴投影:极点既不在两极上又不在赤道上,或投影面的中心线与地轴斜交。
(3)横轴投影:极点在赤道上,或投影面的中心线与地轴垂直。

4 常见投影地图
4.1 世界地图
4.1.1 中国版世界地图

4.1.2 欧洲版世界地图

4.1.3 俄罗斯版世界地图

4.1.4 澳大利亚版世界地图

4.1.5 美国版世界地图

4.1.6 巴西版世界地图

4.1.7 南极版世界地图
4.2 各种投影地图
4.2.1 柏哥斯星状投影



美国地理学家协会(Association of American Geographers,AAG)
4.2.2 彭纳 (Bonne) 投影

4.2.3 等距方位 (Azimuthal equidistant) 投影


联合国会徽
4.2.4 立方体投影

4.2.5 富勒 (Fuller) 投影

富勒地图投影可以折叠成二十面体
4.2.6 温克尔三重 (Winkel Tripel) 投影
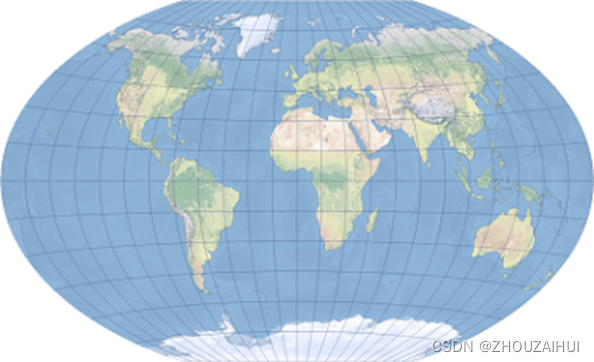

4.2.7 古蒂(Goode)等积投影



陆地


海洋
4.2.8 埃托夫 (Aitoff) 投影

将世界投影到长短轴为2:1的椭圆上
4.2.9 正射 (Orthographic) 投影



4.2.10 墨卡托投影(Mercator)


4.2.11 微信登录界面

NASA蓝色弹珠(Apollo17 1972.12.07) 风云四号A(2017.06.07 13:00)

NASA蓝色弹珠(Apollo17 1972.12.07)
“蓝色弹珠”是在1972年12月7日,阿波罗17号从太空中拍摄的一张照片,这张照片聚集的是南极到地中海,包含着褐色非洲大陆、蓝色的海洋、翻涌的云气,在遥远的太空中,蓝色行星显得美丽非凡却孤独而脆弱。

风云四号A(2017.06.07 13:00)

风云四号A(2017.02.20 13:15)

风云四号B(2021.07.01 12:00)
5 国内常见投影系统
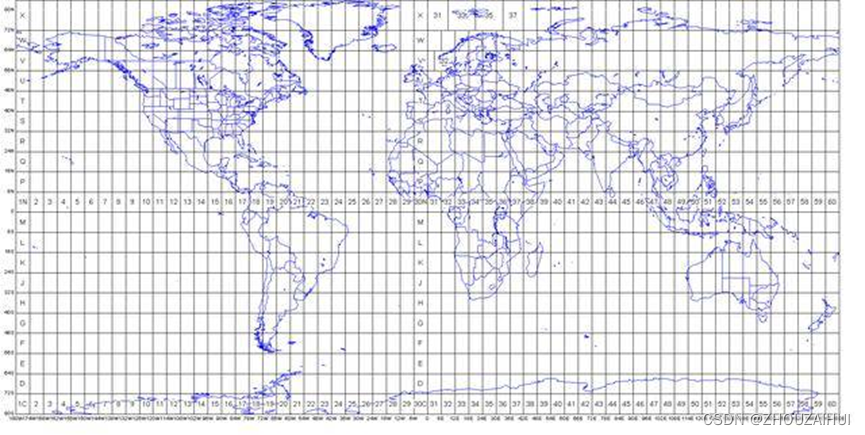
5.1 高斯-克吕格(Gauss-Krüger)投影-等角投影
高斯-克吕格投影是由德国数学家、物理学家、天文学家高斯1820年代拟定,后经德国大地测量学家克吕格1912年对投影公式加以补充,故称为高斯-克吕格投影,又名"等角横切椭圆柱投影”,是地球椭球面和平面间正形投影的一种。 
高斯-克吕格投影是横轴等角切圆柱投影,离开中央子午线越远,变形越大;赤道是直线,离开赤道的纬线是弧线,凸向赤道;没有角度变形;长度和面积变形很小。
高斯投影特点: (1)中央子午线长度变形比为1;(2)在同一条经线上,长度变形随纬度的降低而增大,在赤道处为最大;(3)在同一条纬线上,长度变形随经差的增加而增大,且增大速度较快;(4)在6˚带范围内,长度最大变形不超过0.14%。
高斯-克吕格投影变形控制(分带):

(1)6°带:用于1:2.5万 ~1:50万比例尺地图
起始于初子午线(格林威治),按经差6度为一个投影带自西向东划分,全球共分60个投影带。我国范围可分成11个6度带(13-23)。
(2)3°带:用于大于1:1万比例尺地图
始于东经1°30′,按经差3度为一个投影带自西向东划分,全球共分120个投影带。我国范围可分成22个三度带(24-45)。
5.2 通用横轴墨卡托(UTM)投影
横轴墨卡托投影(Universal Transverse Mercator Grid System)是一种横轴圆柱投影。 中央经线和对向子午线表示为投影中部的一条垂直线。 距中央经线较远的 90° 经线的北部投影为穿过北极的水平直线,其在接近赤道时无限延伸。这些经线的南部投影为穿过南极的水平线,同样无线延伸。 
UTM投影为椭圆柱横正轴割地球椭球体,椭圆柱的中心线位于椭球体赤道面上,且通过椭球体质点。从而将椭球体上的点投影到椭圆柱上。两条割线圆在UTM投影图上长度无变,即2条标准经线圆。两条割线圆之正中间为中央经线圆,中央经线投影后的长度为其投影前的0.9996倍,比例因子k=投影后的长度/投影前的实际长度。则标准割线和中央经线的经度差为1.6206°,即1°37′14.244″。
UTM是由美国制定,因此起始分带并不在本初子午线,而是在180度,因而所有美国本土都处于0-30带内。 将北纬84度至南纬80度之间按经度分为60个带,每带6度UTM投影采用6度分带,从东经180度(或西经180度)开始,自西向东算起,因此1带的中央经线为-177,而0度经线为30带和31带的分界,这两带的分界分别是-3和3度。
UTM 经度区范围为1到60,其中58个区的东西跨度为 6°。经度区涵盖了地球中纬度范围从80°S到84°N之间的所有区域。一共有20个UTM纬度区,每个区的南北跨度为8°;使用字母C到X标识(其中没有字母 I 和 O)。A、B、Y、Z 区不在系统范围以内,它们覆盖了南极和北极区。

5.3 兰伯特(Lambert)投影-等角投影
兰勃特等角圆锥地图投影的球体和椭圆体形式均由Johann H.Lambert于1772年开发。兰勃特等角圆锥地图投影通常基于两个标准纬线,但也可以使用单个标准纬线和比例因子对其进行定义。该投影最适合用于对中纬度东西方向分布的大陆板块进行等角制图。第一次世界大战之前很少使用该投影,但是现在全世界的官方地形制图通常使用该投影。

圆锥投影通常基于两条标准纬线,从而使其成为割投影。超过标准纬线的纬度间距将增加。这是唯一常用的将两极表示为单个点的圆锥投影。
也可使用单条标准纬线和比例尺因子定义。如果比例尺因子不等于1.0,投影实际上将变成割投影。

中国地图的中央经线常位于东经105度,两条标准纬线分别为北纬25度和北纬47度。各省的参数可根据地理位置和轮廓形状初步加以判定。例如甘肃省的参数为:中央经线为东经101度,两条标准纬线分别为北纬34度和41度。

5.4 阿尔伯斯(Albers)投影-等积投影

阿尔伯斯地图投影是一种等积圆锥投影。这种圆锥投影使用两条标准纬线,相比仅使用一条标准纬线的投影,可在某种程度上减少畸变。此投影最适用于中纬度东西方向分布的大陆板块。其通常用于连续的美国、欧洲和澳大利亚的地图。
投影区域面积保持与实地相等。最适合于东西方向分布的大陆板块,不适合南北方向分布的大陆板块。在处理显示400万、100万的全国数据时为了保持等面积特性,经常采用Albers投影。

5. 5 WEB墨卡托(Web Mercator)投影
墨卡托投影,是正轴等角圆柱投影。由荷兰地图学家墨卡托(Gerardus Mercator)于1569年创立。假想一个与地轴方向一致的圆柱切或割于地球,按等角条件,将经纬网投影到圆柱面上,将圆柱面展为平面后,即得本投影。墨卡托投影在切圆柱投影与割圆柱投影中,最早也是最常用的是切圆柱投影。

Google基于墨卡托投影设计了 Web墨卡托投影 (Web Mercator)。Web墨卡托投影使用修改版的墨卡托投影,并已成为Web制图的默认地图投影。此投影的主要区别在于它在所有尺度上都使用球面公式。

将基于椭球体的墨卡托投影简化为“正球体”,精度理论上差别0.33%之内,特别是比例尺越大,地物更详细的时候,差别基本可以忽略。
半球取WGS84椭球体的长半轴 6378137 m。 由于墨卡托圆柱投影的方式必然导致当纬度φ接近两极,即90°时,投影后平面坐标的Y值趋向于无穷大。但沿赤道展开的X轴的范围是固定的,即 [-πr,πr] = [-20037508.342789244,20037508.342789244] 。
为了让投影后的平面能正好在一个正方形内表示,即让投影后的Y轴范围也是[-20037508.342789244,20037508.342789244],反算出纬度的限制范围约为:[-85.05112877980659,85.05112877980659] 。
全世界可以在一个正方形里面刚好放下,也为地图切片的四叉树分割和计算提供了便利。但由于Web墨卡托投影是将原本基于椭球体的墨卡托投影“简化”为了“正球体”。因此,Web墨卡托投影又叫伪墨卡托投影(Pseudo Mercator)、球面投影(Spherical Mercator)。也因为正球体的简化,导致Web墨卡托并非和标准的墨卡托投影一样保持严格的等角(Conformal),而是近似等角。
6 国内常用坐标系统
6.1 北京54坐标系统(BJZ54)
中国成立以后,在全国范围内开展了正规的,全面的大地测量和测图工作,迫切需要建立一个参心大地坐标系。由于当时的"一边倒"政治趋向,故我国采用了前苏联的克拉索夫斯基椭球参数,并与前苏联1942年坐标系进行联测,通过计算建立了我国大地坐标系,定名为1954年北京坐标系。因此,1954年北京坐标系可以认为是前苏联1942年坐标系的延伸。其原点不在北京而是在前苏联的普尔科沃。
6.2 西安80坐标系统(Xian80)
1978年4月在西安召开全国天文大地网平差会议,确定重新定位,建立我国新的坐标系。为此有了1980年国家大地坐标系。1980年国家大地坐标系采用地球椭球基本参数为1975年国际大地测量与地球物理联合会第十六届大会推荐的数据,即IAG 75地球椭球体。该坐标系的大地原点设在我国中部的陕西省泾阳县永乐镇,位于西安市西北方向约60km。
(1)大地原点在我国中部,具体地点是陕西省泾阳县永乐镇;
(2)西安80坐标系是参心坐标系,椭球短轴Z轴平行于地球质心指向地极原点方向,大地起始子午面平行于格林尼治平均天文台子午面;X轴在大地起始子午面内与 Z轴垂直指向经度 0方向;Y轴与 Z、X轴成右手坐标系;
(3)椭球参数采用IUG 1975年大会推荐的参数,因而可得西安80椭球两个最常用的
(4)多点定位;
(5)基准面采用青岛大港验潮站1952-1979年确定的黄海平均海水面(即1985国家高程基准)。


6.3 2000国家大地坐标系统(CGCS2000)
2000中国大地坐标系(China Geodetic Coordinate System 2000,CGCS2000),又称之为2000国家大地坐标系,是中国新一代大地坐标系,21世纪初已在中国正式实施。
2000国家大地坐标系的原点为包括海洋和大气的整个地球的质量中心;2000国家大地坐标系的Z轴由原点指向历元2000.0的地球参考极的方向,该历元的指向由国际时间局给定的历元为1984.0的初始指向推算,定向的时间演化保证相对于地壳不产生残余的全球旋转,X轴由原点指向格林尼治参考子午线与地球赤道面(历元2000.0)的交点,Y轴与Z轴、X轴构成右手正交坐标系。采用广义相对论意义下的尺度。
2000国家大地坐标系是全球地心坐标系在我国的具体体现,其原点为包括海洋和大气的整个地球的质量中心。Z轴指向BIH1984.0定义的协议极地方向(BIH国际时间局),X轴指向BIH1984.0定义的零子午面与协议赤道的交点,Y轴按右手坐标系确定。

6.4 1956黄海高程基准
1956年9月4日,国务院批准试行《中华人民共和国大地测量法式(草案)》,首次建立国家高程基准,称“1956年黄海高程系”,简称“黄海基面”,系以青岛验潮站1950—1956年验潮资料算得的平均海面为零的高程系统。原点设在青岛市观象山验潮站内一间特殊的房屋,这座小石屋全部由崂山花岗岩砌成,顶部中央及四角各竖一石柱,雕凿精细,玲珑别致,室内墙壁上镶一块刻有“中华人民共和国水准原点”的黑色大理石碑,室中有一约2米深的旱井,水袋玛瑙位于旱井底中。小石屋建筑面积7.8平方米,俄式建筑风格,1954年建成。
室内有一直径1米,深10米的验潮井,有三个直径分别为60厘米的进水管与大海相通,每天观测三次,时间分别为:7h45m~8h00m,13h45m~14h00m,19h45m~20h00m,长年观测,从不间断。根据验潮站长年获取的潮位资料,经多次严格的测量计算,得到青岛验潮站海平面为2.429米,将它作为我国高程基准,从这里起算,测得位于青岛市观象山中巅的一幢小石屋里旱井底部一块球形标志物——水袋玛瑙的顶端的主赂为72.260米,地理坐标为东经120°19′08〃,北纬36°04′10〃,国家测绘局将它确定为“中华人民共和国水准原点”。这一水准点便是我国的海拔起点。全国的海拔高度都以这一原点为高程起点进行测量,然后加上72.260米,便得到海拔高度。



水准原点
由于国家水准原点实际高程并非为海拔0米,经国家测绘局批准,由专家精确移植水准原点信息数据,在青岛银海大世界内建起了“中华人民共和国水准零点”(2006)。水准零点标志雕塑,高6米,重10余吨,底座像一个铅锤,寓意老一辈测量人工作的辛苦,顶部地球仪上有6个小圆球,寓意世界上6个著名的海拔原点。在零点雕塑的下面是一个观测井,观测井的底部设有一个价值不菲的巨大的红色玛瑙球,这个球体的顶平面就是我们国家海拔0米的地方。


水准零点
6.5 1985国家高程基准
1956年黄海高程系统为中国第一个国家高程系统,从而结束了过去高程系统繁杂的局面。但由于计算这个基面所依据的青岛验潮站的资料系列(1950年~1956年)较短等原因,中国测绘主管部门决定重新计算黄海平均海面,以青岛验潮站1952年~1979年的潮汐观测资料为计算依据,叫“1985国家高程基准”,并用精密水准测量位于青岛的中华人民共和国水准原点,得出1985年国家高程基准高程和1956年黄海高程的关系为:1985年国家高程基准高程=1956年黄海高程-0.029m。1985年国家高程基准已于1987年5月开始启用,1956年黄海高程系同时废止。1956黄海高程水准原点的高程是72.289米。1985国家高程系统的水准原点的高程是72.260米。习惯说法是"新的比旧的低0.029m",黄海平均海平面是"新的比旧的高"。
由于潮汐存在波长为19年的周期变化,所以高程基准应采用19年的观测数据进行计算。其实,1985国家高程基准就是这么计算来的。具体计算方法是:根据1952年~1979年的潮汐观测资料,计算时取19年的资料为一组, 滑动步长为1年,得到10组以19年为一个周期的平均海面, 取均值得到的结果作为黄海平均海水面,然后再推算出水准原点的高程。
6.6 WGS84坐标系统
一种国际上采用的地心坐标系。坐标原点为地球质心,其地心空间直角坐标系的Z轴指向BIH (国际时间服务机构)1984.O定义的协议地球极(CTP)方向,X轴指向BIH 1984.0的零子午面和CTP赤道的交点,Y轴与Z轴、X轴垂直构成右手坐标系,称为1984年世界大地坐标系统。

WGS84是为 GPS 全球定位系统建立的坐标系统,是世界上第一个统一的地心坐标系,因此也被称为大地坐标系、原始坐标系。一般通过GPS记录仪记录下来的经纬度,就是基于WGS84坐标系的数据。
6.7 GCJ-02坐标系统(高德地图、腾讯地图等)
GCJ-02是由中国国家测绘局(G表示Guojia国家,C表示Cehui测绘,J表示Ju局)制订的地理信息系统的坐标系统。
GCJ-02其实就是对真实坐标系统进行人为的加偏处理,按照特殊的算法,将真实的坐标加密成虚假的坐标,而这个加偏并不是线性的加偏,所以各地的偏移情况都会有所不同。而加密后的坐标也常被大家称为“火星坐标系统”。
国内出版的各种地图系统(包括电子形式),必须至少采用GCJ-02对地理位置进行首次加密。
GCJ-02坐标系统分为GCJ-02经纬度坐标和GCJ-02 WEB墨卡托平面坐标。
6.8 BD-09坐标系统(百度地图)
D09经纬度投影属于百度坐标系,它是在标准经纬度的基础上进行GCJ-02加偏之后,再加上百度自身的加偏算法,也就是在标准经纬度的基础之上进行了两次加偏。
GCJ-02坐标系统分为GCJ-02经纬度坐标和GCJ-02 WEB墨卡托平面坐标。
主流地图在各个地区使用的坐标系
| 地图 | 大陆地区 | 台湾省 | 其它地区 |
| | GCJ-02 | WGS84 | WGS84 |
| 百度 | BD-09 / GCJ-02 | BD-09 / GCJ-02 | WGS84 |
| 高德 | GCJ-02 | WGS84 | WGS84 |
国测局规定:互联网地图在国内必须至少使用GCJ-02进行首次加密,不允许直接使用 WGS84坐标下的地理数据,同时任何坐标系均不可转换为WGS84坐标。因此不存在将GCJ-02坐标转换为WGS84坐标的官方转换方法。
7 投影(平面)坐标系统(以高斯投影为例)
7.1 投影类型

7.2 我国常用的投影方式
7.2.1 全国投影参数
| 地图类型 | 所用投影 | 主要技术参数 |
| 中国全图 | 斜轴等积方位投影、斜轴等角方位投影 | 投影中心: φ0=27°30′,λ0=+105° 或φ0=30°00′,λ0=+105° 或φ0=35°00′,λ0=+105° φ为纬度,λ为经度 |
| 中国全图 (南海诸岛插图) | 正轴等积割圆锥投影 (Albers投影) | φ1=24°00′,φ2=48°00′ 或φ1=25°00′,φ2=45°00′ 或φ1=23°30′,φ2=48°30′ |
| 正轴等角割圆锥投影(Lambert投影)--目前常采用 | 双标准纬线:φ1=25°00′,φ2=47°00′;中央经线:105°E,起算纬度:0° | |
| 中国分省(区)地图(海南省除外) | 正轴等积割圆锥投影(Albers投影)、正轴等角割圆锥投影(Lambert投影) | 各省区图分别采用各自标准纬线 |
| 中国分省(区)地图(海南省-包括南海诸岛) | 正轴等角割圆柱投影(Mercator投影) | |
| 国家基本分幅比例尺地形图 1:100万 | 正轴等角割圆锥投影(Lambert投影) | 按照国际标准4°×6°分幅,标准纬线:φ1=φS+35′,φ2=φN-35′ φS表示北边纬线;φN表示南边纬线 |
| 国家基本分幅比例尺地形图 1:50万-1:2.5万 | 高斯-克吕格投影(Gauss-Krüger投影) | 投影带:13-23,中央子午线:6N-3, N为6°带带号 |
| 国家基本分幅比例尺地形图 1:1万及其以上 | 高斯-克吕格投影(Gauss-Krüger投影) | 投影带:24-45,中央子午线:3n,n为3°带带号 |
| 城市地图 1:5000-1:500 | 城市坐标或城市坐标的高斯投影 |
7.2.2 中国分省投影参数
(1)我国绝大多数省/自治区处于中低纬度地区,最适宜采用圆锥投影(正轴等角圆锥投影);对于个别省/自治区,如广东省包括南海诸岛及南中国海域位于赤道区域,可采用正轴圆柱投影(正轴等角割圆柱投影);对于经差较小的地区,亦可采用高斯-克吕格投影。
| 省/自治区 | 绘图范围 | 标准纬线 | ||||
| 纬度Min | 纬度Max | 经度Min | 经度Max | φ1 | φ2 | |
| 北京市、天津市、河北省 | 36°00′ | 42°40′ | 113°30′ | 120°00′ | 37°30′ | 41°00′ |
| 内蒙古 | 37°30′ | 53°30′ | 97°00′ | 127°00′ | 40°00′ | 51°00′ |
| 山西省 | 34°33′ | 40°45′ | 110°00′ | 114°40′ | 36°00′ | 40°00′ |
| 辽宁省 | 38°40′ | 43°30′ | 118°00′ | 126°00′ | 40°00′ | 42°00′ |
| 吉林省 | 40°50′ | 46°15′ | 121°55′ | 131°30′ | 42°00′ | 46°00′ |
| 黑龙江省 | 43°00′ | 54°00′ | 120°00′ | 136°00′ | 46°00′ | 51°00′ |
| 上海市、江苏省 | 30°40′ | 35°20′ | 116°00′ | 122°30′ | 31°30′ | 34°00′ |
| 浙江省 | 27°00′ | 31°30′ | 118°00′ | 123°30′ | 28°00′ | 30°30′ |
| 安徽省 | 29°20′ | 34°40′ | 114°40′ | 119°50′ | 30°30′ | 33°30′ |
| 江西省 | 24°30′ | 30°30′ | 113°30′ | 118°30′ | 26°00′ | 29°00′ |
| 福建省 | 23°20′ | 28°40′ | 115°40′ | 120°50′ | 24°00′ | 27°30′ |
| 山东省 | 34°10′ | 38°40′ | 114°20′ | 122°40′ | 35°00′ | 37°00′ |
| 广东省 | 18°10′ | 25°30′ | 108°40′ | 117°30′ | 19°30′ | 24°30′ |
| 广西省 | 20°50′ | 26°30′ | 104°30′ | 112°00′ | 22°30′ | 25°30′ |
| 湖北省 | 29°00′ | 33°20′ | 108°30′ | 116°20′ | 30°30′ | 32°30′ |
| 湖南省 | 24°30′ | 30°10′ | 108°40′ | 114°20′ | 26°00′ | 29°00′ |
| 河南省 | 31°23′ | 36°21′ | 110°20′ | 116°40′ | 32°30′ | 35°30′ |
| 四川省 | 26°00′ | 34°00′ | 97°20′ | 110°10′ | 27°30′ | 33°00′ |
| 云南省 | 21°30′ | 29°20′ | 97°20′ | 106°30′ | 22°00′ | 28°30′ |
| 贵州省 | 24°30′ | 29°30′ | 103°30′ | 109°30′ | 25°20′ | 28°30′ |
| 西藏自治区 | 26°30′ | 36°30′ | 78°00′ | 99°00′ | 27°30′ | 35°00′ |
| 陕西省 | 31°40′ | 39°40′ | 105°40′ | 111°00′ | 33°00′ | 38°00′ |
| 甘肃省 | 32°30′ | 42°50′ | 92°10′ | 108°50′ | 34°00′ | 41°00′ |
| 青海省 | 31°30′ | 39°30′ | 89°30′ | 103°10′ | 33°30′ | 38°00′ |
| 新疆自治区 | 34°00′ | 49°10′ | 70°00′ | 96°00′ | 36°30′ | 48°00′ |
| 宁夏自治区 | 35°10′ | 39°30′ | 104°10′ | 107°40′ | 36°00′ | 39°00′ |
| 台湾省 | 21°50′ | 25°30′ | 119°30′ | 122°30′ | 22°30′ | 25°00′ |
注:北京市、天津市标准纬线同河北省,上海市标准纬线同江苏省,南海诸岛采用正轴圆柱投影 :北京市、天津市标准纬线同河北省,上海市标准纬线同江苏省,南海诸岛采用
(2)将相近的同纬度省/自治区合用一个投影,把全国各省/自治区分别采用若干个正轴等角圆锥投影,计算得到正轴等角圆锥投影时长度变形小于0.5%。
| 省/自治区 | 标准纬线 | 最大长度变形(%) | |
| φ1 | φ2 | ||
| 黑龙江 | 45°00′ | 52°30′ | 0.2 |
| 吉林、辽宁 | 40°00′ | 45°30′ | 0.2 |
| 内蒙古 | 39°00′ | 46°00′ | 0.4 |
| 河北、山东、山西、陕西、甘肃、宁夏、青海 | 33°00′ | 42°00′ | 0.03 |
| 新疆 | 36°30′ | 48°00′ | 0.5 |
| 湖北、江苏、安徽、河南 | 30°00′ | 35°30′ | 0.1 |
| 四川、西藏 | 27°30′ | 35°00′ | 0.2 |
| 湖南、浙江、福建、江西、贵州 | 25°00′ | 30°30′ | 0.2 |
| 云南 | 22°00′ | 38°30′ | 0.3 |
| 广东、广西、台湾 | 21°00′ | 25°30′ | 0.2 |
7.3 投影分带
我国基本比例尺地形图主要采用高斯-克吕格投影(Gauss-Kruger)(1:100万除外,1:100万采用正轴等角割圆锥投影,又叫兰勃特投影(Lambert Conformal Conic)),根据不同的比例尺采用不同的投影分带。
按国家规定我国1:2.5-1:50万地形图均采用6度分带;1:1万及更大比例尺地形图采用3度分带,以保证必要的精度。
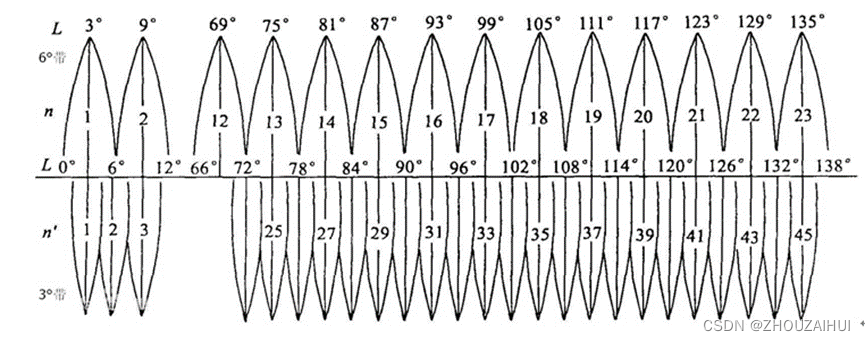
高斯克吕格投影采用分带来减小投影的形变,所以选择投影的时候根据中央经线来选取分带号。6度分带中中国处于13带到23带中,共12个带之间。在3度分带中,中国处于24带到45带共22带之间。中国的地形图范围是75到135°。
| 6度带 | 3度带 | ||||
| 带号 | 中央子午线 | 经度范围 | 带号 | 中央子午线 | 经度范围 |
| 13 | 75° | 72°-78° | 24 | 72° | 70.5°-73.5° |
| 25 | 75° | 73.5°-76.5° | |||
| 14 | 81° | 78°-84° | 26 | 78° | 76.5°-79.5° |
| 27 | 81° | 79.5°-82.5° | |||
| 15 | 87° | 84°-90° | 28 | 84° | 82.5°-85.5° |
| 29 | 87° | 85.5°-88.5° | |||
| 16 | 93° | 90°-96° | 30 | 90° | 88.5°-91.5° |
| 31 | 93° | 91.5°-94.5° | |||
| 17 | 99° | 96°-102° | 32 | 96° | 94.5°-97.5° |
| 33 | 99° | 97.5°-100.5° | |||
| 18 | 105° | 102°-108° | 34 | 102° | 100.5°-103.5° |
| 35 | 105° | 103.5°-106.5° | |||
| 19 | 111° | 108°-114° | 36 | 108° | 106.5°-109.5° |
| 37 | 111° | 109.5°-112.5° | |||
| 20 | 117° | 114°-120° | 38 | 114° | 112.5°-115.5° |
| 39 | 117° | 115.5°-118.5° | |||
| 21 | 123° | 120°-126° | 40 | 120° | 118.5°-121.5° |
| 41 | 123° | 121.5°-124.5° | |||
| 22 | 129° | 126°-132° | 42 | 126° | 124.5°-127.5° |
| 43 | 129° | 127.5°-130.5° | |||
| 23 | 135° | 132°-138° | 44 | 132° | 130.5°-133.5° |
| 45 | 135° | 133.5°-136.5° | |||
带号及中央经线的计算方法
(1)6°带
带号(N)=int(L/6 +1)
中央子午线经度:λ =6N-3
(2)3°带
带号(n)=int(L/3+0.5)
中央子午线经度:λ=3n
7.4 投影坐标定义
7.4.1 高斯-克吕格(Gauss-Kruger)投影平面坐标
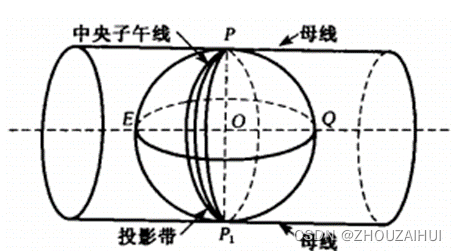
高斯投影时,设想取一个空心圆柱体与地球椭球体相切于某一投影带的中央子午线。在球面图形与圆柱面图形保持等角的条件下,将球面图形投影到圆柱面上,然后将圆柱体沿着南北极的母线切开并展开成平面。
展开的平面中,中央子午线与赤道成为相互垂直的直线,分别作为高斯平面的直角坐标系的纵轴(X轴)和横轴Y轴,同时中央子午线与赤道的交点定义为坐标原点O(0,0),形成测量坐标系。这与几何坐标系(笛卡尔坐标系)坐标轴向定义不同。

但是上述坐标系的定义会使得坐标值出现负值的情况,不利于处理数据,因此需要将X和Y坐标都变为正值,这就需要重新调整坐标系。
(1)北半球
将中央子午线向西偏移500km做平行线,平行线与赤道的交点定义为新的坐标原点O(0,0),坐标系X、Y轴轴向保持不变。
(2)南半球
将中央子午线向西偏移500km做平行线,将赤道向南偏移10000km做平行线,两条平行线交点作为新的坐标原点O(0,0),坐标系X、Y轴轴向保持不变。


我国大陆区域都位于北半球,X坐标都为正值,因此在考虑坐标系的时候只需要Y坐标,使其变为正值即可。
如上图(a)中所示,X坐标是指偏移离开赤道的距离,都为正值;Y坐标是指偏移离开中央子午线的距离,同时偏移方向可以在西侧,也可以在东侧,因此Y坐标可正可负。
图(a)中:ya=+37585m yb=-36262m
图(b)中:ya=+37585+500000=537585m yb=-36262+500000=463738m
同时为了确定这个点到底位于哪个投影带中,因此可以在Y坐标值前面加上改点位于的投影带的带号。假设改点所处3°带的37 带内,则上述两点的Y坐标值为:
ya=37537585m yb=37463738m
7.4.2 独立平面直角坐标
当测量区域较小时,可以把该区域的地球表面当做平面处理,并在该平面上简历独立平面直角坐标系。该坐标系的原点一般选在测区西南角使得所有坐标值均为正值,坐标系的原点可以是假定坐标值。

7.4.3 高斯平面直角坐标(测量坐标)与笛卡尔坐标(几何坐标)异同
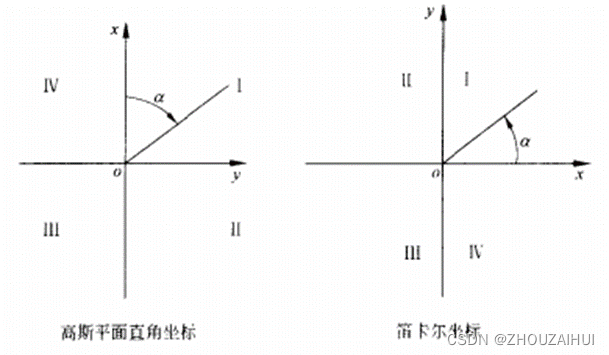
(1)高斯平面坐标中纵坐标为x,正向指北;高斯平面坐标中横坐标为y,正向指东。笛卡尔坐标纵坐标为y,横坐标为x,正好相反。
(2)表示直线方向的方位角定义不同,高斯平面坐标系是以纵坐标x北端起算,顺时针方向量算到直线的角度(测量学中称之为方位角);而笛卡尔坐标是以横轴x东端起算,逆时针测量角度值。
(3)坐标象限不同。高斯平面直角坐标以北东为第一象限,顺时针划分为四个象限;笛卡尔坐标也是以北东为第一象限,逆时针划分为四个象限。
8 ArcGIS Pro中的坐标系统
8.1 国际上定义坐标系统的主要组织
8.1.1 ESPG
European Petroleum Survey Group(欧洲石油调查小组)是一个涉及测地学、测量、制图学与石油勘探相关的科学组织,它成立于1986年,并在2005年重组为OGP(Internation Association of Oil & Gas Producers),EPSG于1985年由吉恩-帕特里克·吉尔比格(Jean-Patrick GIRBIG)创建,并在4年时间里由他担任主席。最初的目标是改善和共享世界各地的位置数据。1994年,Jean-Patrick GIRBIG成功创建了APSG,它是EPSG的美国版。
EPSG其实是一个科学组织,它负责发布并维护坐标参照系统的数据集参数,以及坐标转换描述,该数据集被广泛接受并使用,我们常见的例如EPSG:4326是坐标参考系统中常用的一个坐标系编号(ESPG code)。
以 PROJCS["WGS 84 / UTM zone 50N"] ( WGS1984地理坐标,统一横轴墨卡托(UTM)投影,中间经线117E的投影坐标系) 的 WKT (Well Known Text) 形式为例来解释:
PROJCS["WGS 84 / UTM zone 50N",
GEOGCS["WGS 84", DATUM["WGS_1984", SPHEROID["WGS 84", 6378137, 298.257223563, AUTHORITY["EPSG", "7030"]], AUTHORITY["EPSG", "6326"]], PRIMEM["Greenwich", 0,
AUTHORITY["EPSG", "8901"]], UNIT["degree", 0.0174532925199433, AUTHORITY["EPSG", "9122"]], AUTHORITY["EPSG", "4326"]],
PROJECTION["Transverse_Mercator"],
PARAMETER["latitude_of_origin", 0],
PARAMETER["central_meridian", 117],
PARAMETER["scale_factor", 0.9996],
PARAMETER["false_easting", 500000],
PARAMETER["false_northing", 0],
UNIT["metre", 1, AUTHORITY["EPSG", "9001"]],
AUTHORITY["EPSG", "32650"]]
AUTHORITY["EPSG", "9122"] 指的是EPSG数据集中UNIT为degree的ID是9122;
AUTHORITY["EPSG", "4326"]指的是地理坐标系WGS 84的ID是4326;
AUTHORITY["EPSG", "9001"]指的是EPSG中UNIT为meter的ID是9001;
AUTHORITY["EPSG", "32650"]指的是该投影坐标系WGS 84 / UTM zone 50N的ID是32650。
其他的类似,下表示意相关ID的取值范围。在进行简单操作时调用数据库可能显得麻烦,ProjNET为我们提供了一个SRID.csv文件,
文件中每一行对应一个坐标系,每行又SRID和对应坐标系的WKT形式组成。因此可以很方便地通过SRID来获取地理坐标系或投影坐标系,
《Loading a projection by Spatial Reference ID》提供了一个SridReader类来实现GetCSbyID返回相应坐标系的功能。
SRID.csv和SRIDReader.cs在ProjNET源码和示例中可下载得到。
8.1.2 OGC
Open Geospatial Consortium,自称是一个非盈利的、国际化的、自愿协商的标准化组织,它的主要目的就是制定与空间信息、基于位置服务相关的标准。这些标准就是OGC的“产品”,而这些标准的用处就在于使不同厂商、不同产品之间可以通过统一的接口进行互操作。
SRID(Spatial Reference System Identifier)就是OGC标准中关于空间参考系统标识码。
在OGC标准中的SFS(OpenGIS® Simple Features Interface Standard)-简单要素标准,其中就包括了我们平时所熟知的WKT、WKB,WKT可以描述的几何对象,也可以描述的空间参考;
WKT(Well-known Text)可以通过文本来描述几何对象。
GEOGCS[
"GCS_WGS_1984",
DATUM["D_WGS_1984",SPHEROID["WGS_1984",6378137,298.257223563]],
PRIMEM["Greenwich",0],
UNIT["Degree",0.017453292519943295],
AUTHORITY["EPSG","4326"]]

OGC标准中的参数SRID,也是指的空间参考系统的ID,与EPSG一致
8.1.3 ESRI
在Arcgis API中通过WKID作为坐标参考系统的标识;所以WKID常用于Arcgis二次开发中。例如WKID=4326表示WGS84地理坐标系;

投影坐标系 CGCS2000 3 Degree GK CM 108E
投影 Gauss Kruger
WKID 4545
授权 EPSG
线性单位 米 (1.0)
东偏移量 500000.0
北偏移量 0.0
中央经线 108.0
比例因子 1.0
起始纬度 0.0
地理坐标系 China Geodetic Coordinate System 2000
WKID 4490
授权 EPSG
角度单位 Degree (0.0174532925199433)
本初子午线 Greenwich (0.0)
基准面 D China 2000
参考椭球体 CGCS2000
长半轴 6378137.0
短半轴 6356752.314140356
扁率 298.257222101
WKT形式表示该投影坐标系:
PROJCS["CGCS2000_3_Degree_GK_CM_108E",
GEOGCS["GCS_China_Geodetic_Coordinate_System_2000",
DATUM["D_China_2000",
SPHEROID["CGCS2000",6378137.0,298.257222101]],
PRIMEM["Greenwich",0.0],
UNIT["Degree",0.0174532925199433]],
PROJECTION["Gauss_Kruger"],
PARAMETER["False_Easting",500000.0],
PARAMETER["False_Northing",0.0],
PARAMETER["Central_Meridian",108.0],
PARAMETER["Scale_Factor",1.0],
PARAMETER["Latitude_Of_Origin",0.0],
UNIT["Meter",1.0],
AUTHORITY["EPSG",4545]]

8.1.4 结论
EPSG CODE(EPSG)、SRID(OGC)和WKID(ESRI)分别属于不同组织、公司制定的标识符,都是用于标识空间参考系统,三者对同一空间参照系统的ID是一样。
8.2 高斯-克吕格投影


8.3 Lambert等角投影


8.4 Albers等积投影

8.5 UTM投影

8.6 WEB墨卡托投影