先来点题目看看
1031. 两个非重叠子数组的最大和
难度中等249收藏分享切换为英文接收动态反馈
给你一个整数数组 nums 和两个整数 firstLen 和 secondLen,请你找出并返回两个非重叠 子数组 中元素的最大和,长度分别为 firstLen 和 secondLen 。
长度为 firstLen 的子数组可以出现在长为 secondLen 的子数组之前或之后,但二者必须是不重叠的。
子数组是数组的一个 连续 部分。
示例 1:
输入:nums = [0,6,5,2,2,5,1,9,4], firstLen = 1, secondLen = 2 输出:20 解释:子数组的一种选择中,[9] 长度为 1,[6,5] 长度为 2。
示例 2:
输入:nums = [3,8,1,3,2,1,8,9,0], firstLen = 3, secondLen = 2 输出:29 解释:子数组的一种选择中,[3,8,1] 长度为 3,[8,9] 长度为 2。
示例 3:
输入:nums = [2,1,5,6,0,9,5,0,3,8], firstLen = 4, secondLen = 3 输出:31 解释:子数组的一种选择中,[5,6,0,9] 长度为 4,[0,3,8] 长度为 3。
提示:
1 <= firstLen, secondLen <= 10002 <= firstLen + secondLen <= 1000firstLen + secondLen <= nums.length <= 10000 <= nums[i] <= 1000
我本来的想法很是暴力,绝对过不了
于是我看了题解,直接点醒我了,哇
还是那句话,看懂了等于我会了
1我们可以把他看出两部分假设l在r的前面,我们可以看成,以r的左端口为界限,r+secndlen个数的和加上dp[前r左端口]最大的部分和,我们只要求dp数组即可
2我们还要遍历r的左端口的全部位置,但是要在l的后面的最大值
你会问为啥r一定要在后面,我来解答,把r和l的位置换一下再来一遍比较最大值
两个最大值取最大就是答案
int max(int j,int y)
{
if(j>y){
return j;
}
else{
return y;
}
}
int maxSumTwoNoOverlap(int* nums, int numsSize, int firstLen, int secondLen)
{
int a[1010];
a[0]=nums[0];
for(int k=1; k<numsSize; k++)
a[k]=a[k-1]+nums[k];
int dp1[1010]= {0};
int dp2[1010]={0};
int maxr=0;
int maxr1=0;
dp1[firstLen]=a[firstLen-1];//dp的起点前面的是0,长度都没折磨长
for(int j=firstLen+1; j<numsSize; j++)
{
dp1[j]=max(dp1[j-1],a[j-1]-a[j-firstLen-1]);
}
maxr=dp1[numsSize-secondLen]+a[numsSize-1]-a[numsSize-1-secondLen];
for(int j=numsSize-secondLen-1;j>=firstLen;j--){
maxr=max(maxr,dp1[j]+a[j+secondLen-1]-a[j-1]);
}
dp2[secondLen]=a[secondLen-1];//dp的起点前面的是0,长度都没折磨长
for(int j=secondLen+1; j<numsSize; j++)
{
dp2[j]=max(dp2[j-1],a[j-1]-a[j-secondLen-1]);
}
maxr1=dp2[numsSize-firstLen]+a[numsSize-1]-a[numsSize-1-firstLen];
for(int j=numsSize-firstLen-1;j>=secondLen;j--){
maxr1=max(maxr1,dp2[j]+a[j+firstLen-1]-a[j-1]);
}
return max(maxr,maxr1);
}动态规划就是,奇怪,思路逆天,没写过,好难想
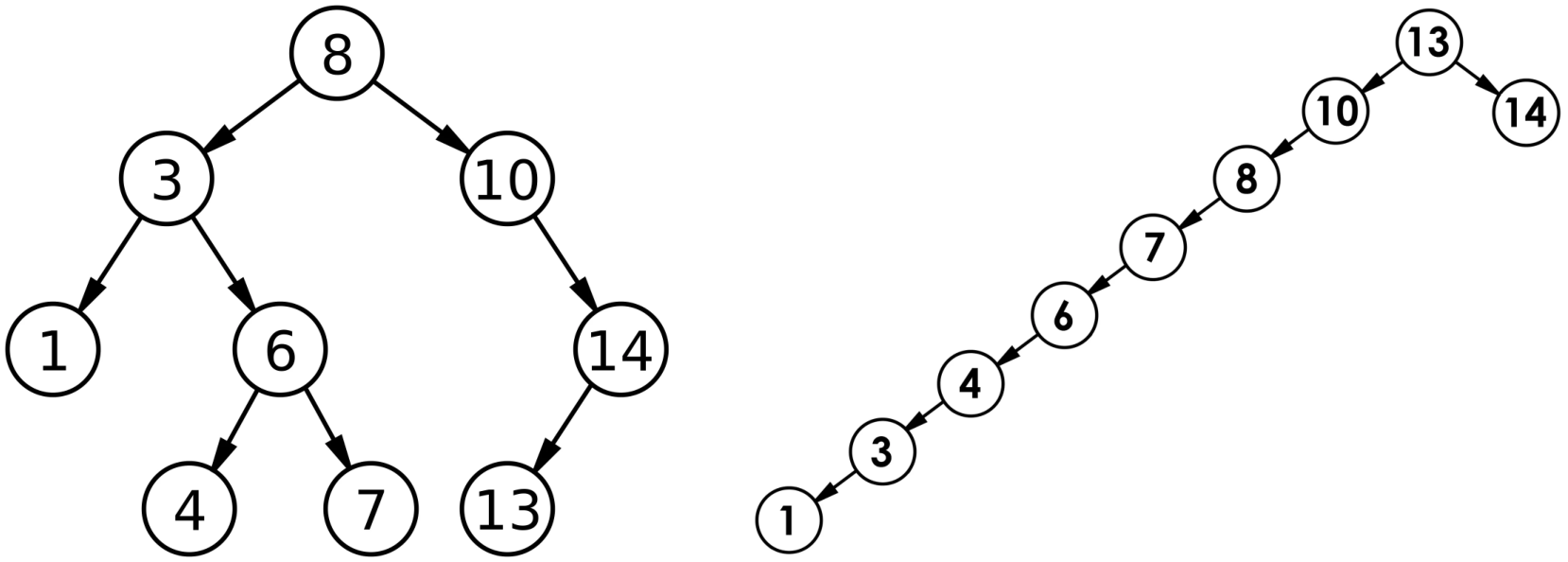
110. 平衡二叉树
难度简单1315收藏分享切换为英文接收动态反馈
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:true
示例 2:
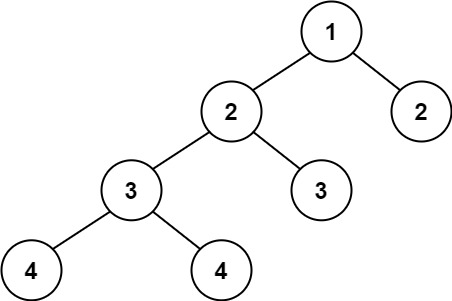
输入:root = [1,2,2,3,3,null,null,4,4] 输出:false
示例 3:
输入:root = [] 输出:true
提示:
- 树中的节点数在范围
[0, 5000]内 -104 <= Node.val <= 104
和昨天那题目有点像,但是跟简单一点,没有奇怪的情况,这就是一个向下搜索,得到树的搞度(每个节点都要判断,只要有一节点不满足,就是不满足的返会false)
看代码(递归求树的高度因该都会吧)
int max(int a,int b){
if(a>b)
return a;
else
return b;
}
int dfs(struct TreeNode* root,int* l){
if(root==NULL){
return 0;
}
int ll=dfs(root->left,l)+1;
int r=dfs(root->right,l)+1;
if(abs(ll-r)>1){
*l=0;
}
return max(ll,r);
}
bool isBalanced(struct TreeNode* root){
int l=1;
dfs(root,&l);
if(l==1)
return true;
else
return false;
}1594. 矩阵的最大非负积
难度中等45收藏分享切换为英文接收动态反馈
给你一个大小为 m x n 的矩阵 grid 。最初,你位于左上角 (0, 0) ,每一步,你可以在矩阵中 向右 或 向下 移动。
在从左上角 (0, 0) 开始到右下角 (m - 1, n - 1) 结束的所有路径中,找出具有 最大非负积 的路径。路径的积是沿路径访问的单元格中所有整数的乘积。
返回 最大非负积 对 109 + 7 取余 的结果。如果最大积为 负数 ,则返回 -1 。
注意,取余是在得到最大积之后执行的。
示例 1:
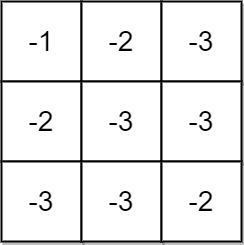
输入:grid = [[-1,-2,-3],[-2,-3,-3],[-3,-3,-2]] 输出:-1 解释:从 (0, 0) 到 (2, 2) 的路径中无法得到非负积,所以返回 -1 。
示例 2:
输入:grid = [[1,-2,1],[1,-2,1],[3,-4,1]] 输出:8 解释:最大非负积对应的路径如图所示 (1 * 1 * -2 * -4 * 1 = 8)
示例 3:
输入:grid = [[1,3],[0,-4]] 输出:0 解释:最大非负积对应的路径如图所示 (1 * 0 * -4 = 0)
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 15-4 <= grid[i][j] <= 4
这题目我还以为搜索的题目,没想到啊被各种奇奇怪怪捶
今天是没写出来我记住了
今天就写了两个题目,已经开始继续学习java了,直接从方法看到面对对象,这部分很重要,我觉得是要好好学学的
ok今天撒花谢幕
bb