一元线性回归预测模型

实验目的

通过一元线性回归预测模型，掌握预测模型的建立和应用方法，了解线性回归模型的基本原理

实验内容

一元线性回归预测模型

实验步骤和过程

(1)第一步：学习一元线性回归预测模型相关知识。

线性回归模型属于经典的统计学模型，该模型的应用场景是根据已 知的变量（自变量）来预测某个连续的数值变量（因变量）。例如，餐 厅根据每天的营业数据（包括菜谱价格、就餐人数、预定人数、特价菜 折扣等）预测就餐规模或营业额；网站根据访问的历史数据（包括新用 户的注册量、老用户的活跃度、网页内容的更新频率等）预测用户的支 付转化率；医院根据患者的病历数据（如体检指标、药物服用情况、平 时的饮食习惯等）预测某种疾病发生的概率。
站在数据挖掘的角度看待线性回归模型，它属于一种有监督的学习 算法，即在建模过程中必须同时具备自变量x和因变量y。

相关性分析

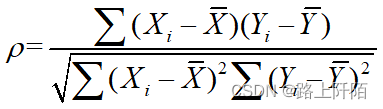
一元线性回归模型

一元线性回归模型也被称为简单线性回归模型，是指模型中只含有一个自变量和一个因变量，用来建模的数据集可以表示成{(x1,y1)，(x2,y2)，……，(xn,yn)}。其中，xi表示自变量x的第i个值，yi表示因变量y的第i个值，n表示数据集的样本量。当模型构建好之后，就可以根据其他自变量x的值，预测因变量y的值，该模型的数学公式可以表示成：
y=a+bx+ε
其中，
a为模型的截距项，
b为模型的斜率项，
ε为模型的误差项。
模型中的a和b统称为回归系数，误差项ε的存在主要是为了平衡等号两边的值，通常被称为模型无法解释的部分。

拟合线的求解

接下来要学会如何根据自变量x和因变量y，求解回归系数a和b。前面已经提到，误差项ε是为了平衡等号两边的值，如果拟合线能够精确地捕捉到每一个点（所有的散点全部落在拟合线上），那么对应的误差项ε应该为0。按照这个思路来看，要想得到理想的拟合线，就必须使误差项ε达到最小。由于误差项是y与a+bx的差，结果可能为正值或负值，因此误差项ε达到最小的问题需转换为误差平方和最小的问题（最小二乘法的思路）。误差平方和的公式可以表示为

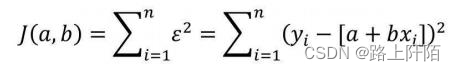
由于建模时的自变量值和因变量值都是已知的，因此求解误差平方和最小值的问题就是求解函数J(a,b)的最小值，而该函数的参数就是回归系数a和b。
该目标函数其实就是一个二元二次函数，如需使得目标函数J(a,b)达到最小，可以使用偏导数的方法求解出参数a和b，进而得到目标函数的最小值。关于目标函数的求导过程如下：

(2)第二步：数据准备，数据来源于课本例题。

序号 x1	年份	水路货运量y
1	1991	1659
2	1992	1989
3	1993	2195
4	1994	2255
5	1995	2329
6	1996	2375
7	1997	2364
8	1998	2354
9	1999	2418
10	2000	2534
11	2001	2568
12	2002	2835

(3)第三步：使用 Python 编写实验代码并做图。

import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 读取Excel文件
data = pd.read_excel('E:\\File\\class\\数据挖掘\\test1.xlsx')
x = data[['年份']]
y = data['水路货运量y']
# 训练模型
model = LinearRegression()
model.fit(x, y)
# 预测值
x_new = [[2004]]
y_pred = model.predict(x_new)
print("预测值为：", y_pred[0])
# 绘制图像
plt.scatter(x, y)
plt.plot(x, model.predict(x), color='r')
plt.xlabel('年份')
plt.ylabel('水路货运量y')
plt.title('一元线性回归预测模型案例')
plt.show()

代码解释：

导入了 sklearn.linear_model 中的 LinearRegression 类，用于构建线性回归模型；

设置了中文字体为 SimHei；

使用 pandas 读取了名为 test1.xlsx 的 Excel 文件，并将年份列作为自变量 x，将水路货运量列作为因变量 y；

使用 LinearRegression 类构建了一个线性回归模型，并使用 fit() 方法拟合了数据；

定义了一个新的自变量 x_new，它的值为 [[2004]]，即预测年份为2004；

使用 predict() 方法预测了 x_new 对应的因变量 y_pred；

输出预测值 y_pred；

使用 matplotlib.pyplot 绘制了数据的散点图和线性回归模型的拟合曲线；

添加了坐标轴标签和标题，并显示了图像。

在上面的代码中，首先使用pd.read_excel()函数读取名为"test1.xlsx"的Excel文件，并将其转化为DataFrame格式的数据存储在data变量中。然后，从data中选择了"x"列和"y"列的数据，并将其转化为numpy数组的形式，分别存储在x和y变量中。接着，使用sklearn中的LinearRegression模型进行训练，得到训练好的模型。然后，构造了一个新的自变量x_new，使用训练好的模型进行预测，得到预测值y_pred。最后，使用matplotlib库绘制了数据散点图和拟合直线图，并添加了x轴标签、y轴标签和图像标题，以便进行可视化分析。

需要注意的是，在使用pd.read_excel()函数读取Excel文件时，需要将文件名和路径指定为正确的文件名和路径。如果Excel文件中有缺失值或格式不规范的数据，需要进行数据清洗和预处理，以保证模型的准确性。

(4)第四步：实验结果。

绘图和预测2004年的水路货运量。

这里的预测结果为：2884.0792540792318