《编程思维与实践》1037.一元多项式乘法

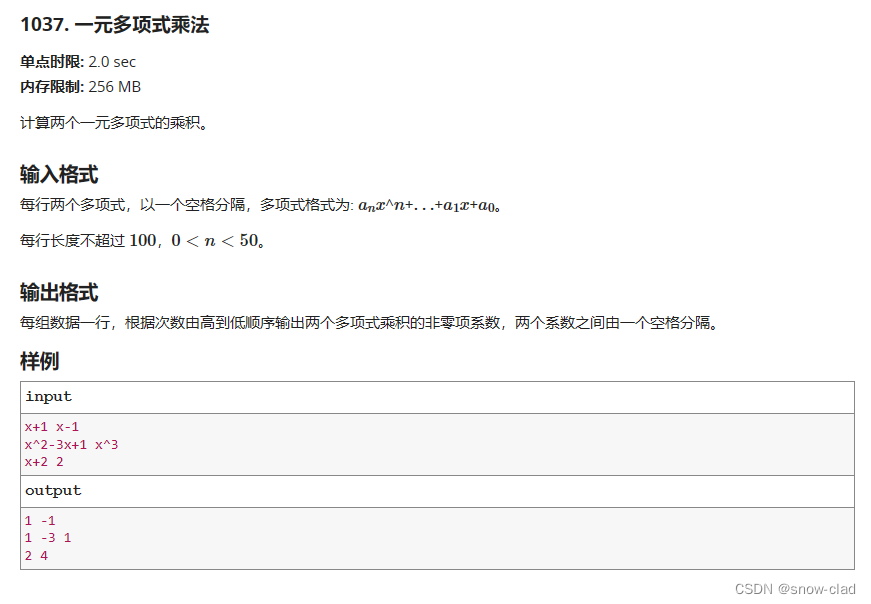
题目

思路

比较容易想到将步骤分为三步:

1.读取多项式每项的系数(coefficient)和对应的指数(dim);

2.进行多项式乘法;

3.输出进行多项式乘法后的非零项系数.

其中多项式乘法可以通过循环来处理,输出可以用if来判断系数是否为0,需要考虑的是如何读取多项式:

ax^y(a≠±1) , ±x^y , ax(a≠±1) , ±x 和 c(常数项) 为每项可能出现的所有情况.

一般情况只需要利用atoi存取系数,如果存完系数后读取的第一个字符不是x,

那表示读取的是常数项,否则直接跳过x,接着再存指数,最后利用指数为数组下标存系数.

注意的点:

1.对于 a＝±1 和 有无 ‘^’ 的情况,用atoi时需要小心.

2.输出的时候指数应该从大到小(逆序).

3.多项式乘法后指数会变大,存结果时数组应该开大一些.

代码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<ctype.h>
#define N 100   //指数小于50

void readpoly(char* s,int* coef)    //polynomial 多项式
{
	while(*s!='\0')
	{
		char temp1[N];  
        char temp2[N];
        int i=0;
        int j=0;
        while(*s!='\0'&&(isdigit(*s)||*s=='+'||*s=='-'))  //注意s别越界（条件写前面） 
        {
            temp1[i++]=*s;
            s++;
        }
        if(i==0||(i==1&&!isdigit(temp1[0])))  //a＝±1的情形
        {
            temp1[i++]='1';
        }
        temp1[i]='\0';
        if(*s!='x')    //是常数项 (0次方)
        {
            coef[0]=atoi(temp1);          
        }
        else         //非常数项
        {
            s++;        //跳过x
            if(*s=='^')    //判断是不是有'^'
            {
            	s++;
                while(isdigit(*s))
                {
                    temp2[j++]=*s;
                    s++;
                }
                temp2[j]='\0';
                coef[atoi(temp2)]=atoi(temp1);
            }
       		else
            {
                coef[1]=atoi(temp1);
            }
        }
	}
}

void multiply(int* coef1,int* coef2,int* result)
{
	for(int i=0;i<N/2;i++)
	{
		for(int j=0;j<N/2;j++)
		{
			result[i+j]+=coef1[i]*coef2[j];
		}
	}
}

void output(int *result)
{ 
	for(int i=N-1;i>=0;i--)    //逆向 
	{
		if(result[i]!=0)
		{
			printf("%d ",result[i]);
		}
	}
	printf("\n");
} 

int main()
{
	char s[101];     //长度不超过100
	while(scanf("%s",s)!=EOF)
	{
		int coef[2][N/2];       //coefficient 系数  
        memset(coef,0,sizeof(coef));
		readpoly(s,coef[0]);
		scanf("%s",s);
		readpoly(s,coef[1]);    
		int result[N]={0};
		multiply(coef[0],coef[1],result);
		output(result); 
	}
	return 0;
}