1049.最后一块石头的重量 II

思路：

本题其实就是尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，这样就化解成01背包问题了。

本题物品的重量为stones[i]，物品的价值也为stones[i]。

对应着01背包里的物品重量weight[i]和物品价值value[i]。

动规五部曲：

1.确定dp数组以及下标的含义:dp[j]将石头放入载重上限为 j 的背包中可以获得的最大价值。

2.确定递推公式：

dp[j] = max(dp[j], dp[j - stone[i-1]] + stone[i-1]);

3.dp数组如何初始化:01背包，一维dp初始化，dp[0] =0

4.确定遍历顺序:如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历

5.举例推导dp数组:

举例，输入：[2,4,1,1]，此时target = (2 + 4 + 1 + 1)/2 = 4 ，dp数组状态图如下：
在这里插入图片描述

一维

class Solution:
    def lastStoneWeightII(self, stones: List[int]) -> int:
        target = sum(stones) // 2
        size = len(stones)
        dp = [0 for _ in range(target+1)]
    	
        #枚举前i种物体
        for i in range(1,size+1):
            # 枚举背包装载重量
            for j in range(target,stones[i-1]-1,-1):
                dp[j] = max(dp[j],dp[j-stones[i-1]]+stones[i-1])
        return sum(stones)-dp[target]-dp[target]

二维

class Solution:
    def lastStoneWeightII(self, stones: List[int]) -> int:
        # 背包
        target = sum(stones) // 2
        size = len(stones)
        dp = [[0 for _ in range(target+1)] for _ in range(size+1)]
    
    	#枚举前i种物体
        for i in range(1,size+1):
            # 逆序枚举背包装载重量（避免状态值错误）
            for j in range(target+1):
                # 第i-1件物品放不下
                if j < stones[i-1]:
                    dp[i][j] = dp[i-1][j]
                else:
                    dp[i][j] = max(dp[i-1][j],dp[i-1][j-stones[i-1]]+stones[i-1])
        return sum(stones)-dp[-1][target]-dp[-1][target]

494.目标和

动态规划

思路：

为target，那么就一定有 left组合 - right组合 = target，left + right = sum，而sum是固定的。right = sum - left

left - (sum - left) = target 推导出 left = (target + sum)/2 。

target是固定的，sum是固定的，left就可以求出来。

x = (target + sum) / 2

此时问题就转化为，装满容量为x的背包，有几种方法。

当(target + sum) % 2 == 1，abs(target)>sum 无解

动规五部曲

1.确定dp数组以及下标的含义: dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法

2.确定递推公式：dp[j] = dp[j] + dp[j - nums[i]]

不使用当前 num：只使用之前元素填满容量为 j 的背包的方法数。
使用当前num：填满容量 j-num的包的方法数，再填入 num的方法数。

3.初始化：初始状态下，默认填满容量为 0 的背包有 1 种办法（什么也不装）,dp[0] = 1

4.遍历顺序：物品外面背包里面，nums放在外循环，target在内循环

5.举例数组：nums: [1, 1, 1, 1, 1], S: 3

bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4

在这里插入图片描述

class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        if (target + sum(nums)) % 2 == 1:return 0
        if (abs(target)>sum(nums)): return 0
        W = (target + sum(nums)) // 2
        dp =[0 for _ in range(W+1)]
        dp[0] = 1
        for i in range(len(nums)):
            for j in range(W,nums[i]-1,-1):
                dp[j] = dp[j] + dp[j-nums[i]]
        return dp[W]

474.一和零

思路：

这个背包有两个维度，一个是m 一个是n，而不同长度的字符串就是不同大小的待装物品。

动规五部曲

1.确定dp数组以及下标的含义: dp[i] [j]：最多有i个0和j个1的strs的最大子集的大小为dp[i] [j]。

2.确定递推公式：dp[i] [j] = max(dp[i] [j], dp[i - zeroNum] [j - oneNum] + 1)

dp[i] [j] 可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。

dp[i] [j] 就可以是 dp[i - zeroNum] [j - oneNum] + 1。

3.初始化：初始为0

4.遍历顺序：外层for循环遍历物品，内层for循环遍历背包容量且从后向前遍历，本题物品就是strs里的字符串，背包容量就是题目描述中的m和n

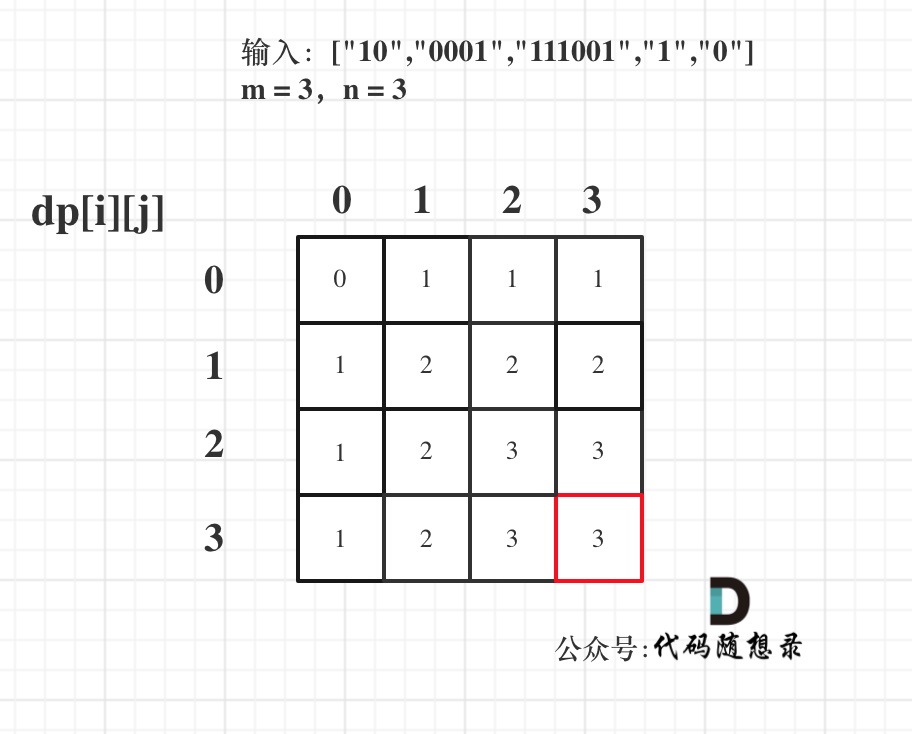
5.举例数组：以输入：[“10”,“0001”,“111001”,“1”,“0”]，m = 3，n = 3为例

最后dp数组的状态如下所示：

474.一和零

class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        dp = [[0 for _ in range(n+1)] for _ in range(m+1)]
        for str in strs:
            zeronums = str.count('0')
            onenums =  str.count('1')
            for i in range(m,zeronums-1,-1):
                for j in range(n,onenums-1,-1):
                    dp[i][j] = max(dp[i][j],dp[i-zeronums][j-onenums]+1)
        return dp[m][n]