一、多重共线性说明

多重共线性一般是指：如果有两个或者多个自变量高度相关（相关系数大于0.8），难以区分一个自变量对因变量的影响和作用，将自变量相关性产生的后果定义为多重共线性，一般提出多重共线性问题，研究者往往会想到回归分析。回归分析方法，回归模型等，在统计学中都占有重要地位，多数情况下，使用回归分析进行构建模型是，由于模型中解释变量之间存在高度相关关系（如相关系数大于0.8），所以导致数据模型估计失真，此时需要消除多重共线性问题，实现模型的精准估计。接下来从多重共线性的诊断，多重共线性解决办法以及举例进行说明多重共线性几个方面进行说明。

二、多重共线性诊断

1.经验法

经验法就是通过宏观经验进行简单的判断，模型的R方比较高，但是变量不显著（回归中的t检验），或者模型结果不合理，这可能存在多重共线性，即如果R方较高，一般情况下方程整体会显著（即通过F检验），但t检验表明，没有或很少有斜率系数是显著不为0的。

2.相关系数检验法

对于模型中任意两个不同的解释变量进行相关分析，得到相关系数，如果相关系数的绝对值较大（一般大于0.8），则认为这两个变量相关性较高，但是需要知道，相关分析只能检验两个解释变量之间的相关性，对于更多（比如三个）解释变量的相关性检验并不适用。

3.VIF（方差膨胀因子法）

 

4.特征根判断法

 

三、解决办法

如果存在多重共线性问题，一般可以从三个方面进行说明，剔除变量、增大样本量以及更换模型。

1.剔除变量

剔除变量是处理共线性最直接的办法。一般可以找出引起多重共线性的解释变量，然后把它从模型中剔除，但是常常不容易判断具体哪一个变量引起的多重共线性，所以一般解决办法有逐步回归法等。逐步回归是在模型中逐个引入解释变量，如果新引入的变量使得模型统计意义检验或者判断与事实相符，并且R方又能提高，则应该引入，反之无需引入。但是，排除引起共线性的变量后，保留在模型中变量的系数估计值将会改变，并且实际意义也会发生变化。

2.增大样本量

一般如果在计量经济模型中，入股变量的样本数据极少，很容易引起多重共线性问题，可以通过手机更多的观测值来增加样本量，可以避免或者减少共线性的影响，但是会引起计算量的增加。

3.更换模型

除此之外，还可以更换研究模型，利用岭回归、主成分回归、Lasso回归等。

岭回归是以引入偏误来减少参数估计量方差的方法，虽然通过岭回归能使数据变的更合理，但是如果是原模型的实际意义不合理，即使通过岭回归修正后也不一定使模型通过实际意义的检验，所以说在实际应用中也不是所有的共线性都可以用岭回归来解决。操作如下：

主成分回归中主成分分析又称主分量分析，他是利用降维的思想，在尽量减少损失的信息的前提下，把多个指标通过正交旋转转化为几个综合的指标的分析方法，其基本原理是：利用主成分分析将解释变量转换成若干个主成分，这些主成分从不同侧面反映了解释变量的综合影响，然后在讲解释变量对这些主成分进行回归，在根绝主成分分与解释变量之间的关系，求得原回归模型的估计方程。比如有6个X，其利用降维原理将6个X降维成比如2个主成分，然后后续再进行分析比如线性回归（此种做法称作主成分回归）。操作如下：

Lasso回归

Lasso回归分析（Lasso Regression）是一种用于解决线性回归分析中自变量共线性的研究算法。针对Lasso回归：其研究步骤共为2步,分别是结合轨迹图寻找最佳K值；输入K值进行回归建模。具体如下：

第一步：Lasso回归分析前需要结合轨迹图确认K值；K值的选择原则是各个自变量的标准化回归系数趋于稳定时的最小K值。K值越小则偏差越小，K值为0时则为普通线性OLS回归；SPSSAU提供K值智能建议，也可通过主观识别判断选择K值；

第二步：对于K值，其越小越好，通常建议小于1，确定好K值后，得出Lasso回归模型估计。操作如下：

虽然岭回归和Lasso回归看起来操作差不多但是二者的原理确大不相同，岭回归是使用L2正则化，Lasso回归是使用L1正则化。接下来举个例子进行说明。

四、举例说明

利用线性回归研究居民消费价格指数y和农村居民消费价格x1，、城市居民消费价格指数x2以及商品零售价格指数x3之间的影响关系。其中数据来源于中国统计局网站（文末有案例数据可以下载）。

1.判断多重共线性

首先判断模型是否存在共线性问题，判断多重共线性的方法有很多这里利用VIF值进行判断。结果如下：

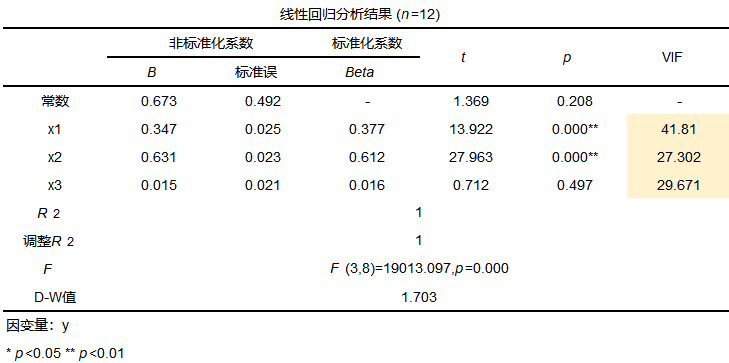
从结果可以看出，VIF值均大于10，所以存在多重共线性，需要进行处理，尽管处理多重共线性的方法有多种，这里选择比较常用的岭回归进行处理。

2.解决多重共线性

利用岭回归处理多重共线性问题，一般有两步分别如下：

1. 岭回归分析前需要结合岭迹图确认K值；K值的选择原则是各个自变量的标准化回归系数趋于稳定时的最小K值。K值越小则偏差越小，K值为0时则为普通线性OLS回归；SPSSAU提供K值智能建议，也可通过主观识别判断选择K值；
2. 对于K值，其越小越好，通常建议小于1；确定好K值后，即可主动输入K值，得出岭回归模型估计。

首先结合岭迹图确认K值：

结果如下：

从上图看出，以居民消费价格指数y为因变量，农村居民消费价格x1，、城市居民消费价格指数x2以及商品零售价格指数x3为自变量做岭回归，图中可以看看出，当K值为0.01时，此时自变量的标准回归系数趋于稳定，所以SPSSAU系统建议将K值取为0.01。

确定好K值后，即可主动输入K值，得出岭回归模型估计。结果如下：

从F检验结果中可以看到p值小于0.05,整体模型有效，至少有一个x对y产生影响，模型有意义。接着进行查看岭回归结果,如下：

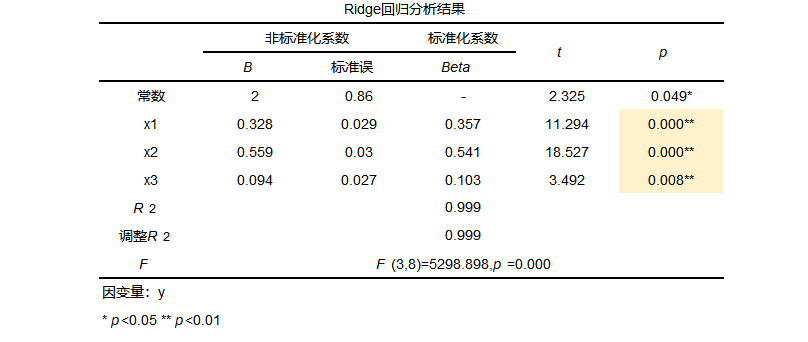
从岭回归的结果中可以看出，模型公式为：y=2.000 + 0.328*x1 + 0.559*x2 + 0.094*x3。并且x1、x2和x3对因变量均有影响（p值均小于0.05）并且标准化系数均大于0所以农村居民消费价格x1，、城市居民消费价格指数x2以及商品零售价格指数x3均对居民消费价格指数y有正向影响的作用。并且0.541>0.357>0.103,所以说明x2对因变量的影响最大。模型的R方为0.999，接近于1，说明模型拟合的非常好。

五、总结

本文最开始介绍了多重共线性，然后进行说明多重共线性如何进行诊断多重共线性，其中包括经验法，相关系数检验法，VIF值以及特征根判断法，并且如果存在多重共线性应该如何解决，可以剔除变量或者增大样本量或者更换模型，举例说明如何解决多重共线性，利用岭回归的方法进行解决，最后得到有效结论。