计算机图形学 | 投影变化
- 计算机图形学 | 投影变化
- 7.1 有趣的投影
- 投影的概念
- 平行投影
- 正投影
- 斜投影
- 透视投影
- 7.2 规范化的投影变换
- 观察的要素
- 观察空间
- 规范化的投影变换
华中科技大学《计算机图形学》课程
MOOC地址:计算机图形学(HUST)
计算机图形学 | 投影变化
7.1 有趣的投影
投影的概念
观察变换中隐含有一个观察平面。
观察平面(ViewPlane),即投影平面。
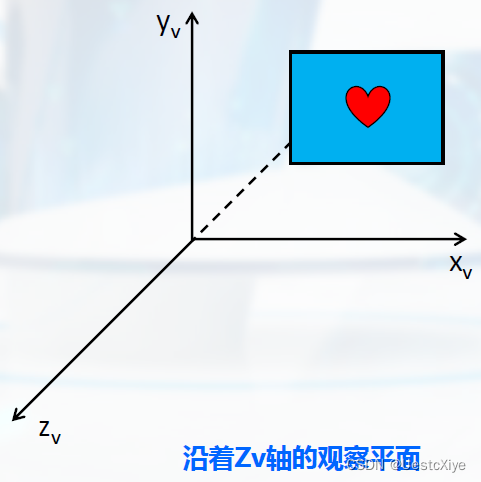
投影方式分为:平行投影和透视投影。


平行投影:
透视投影:
平行投影
平行投影可分成两类:正投影和斜投影。
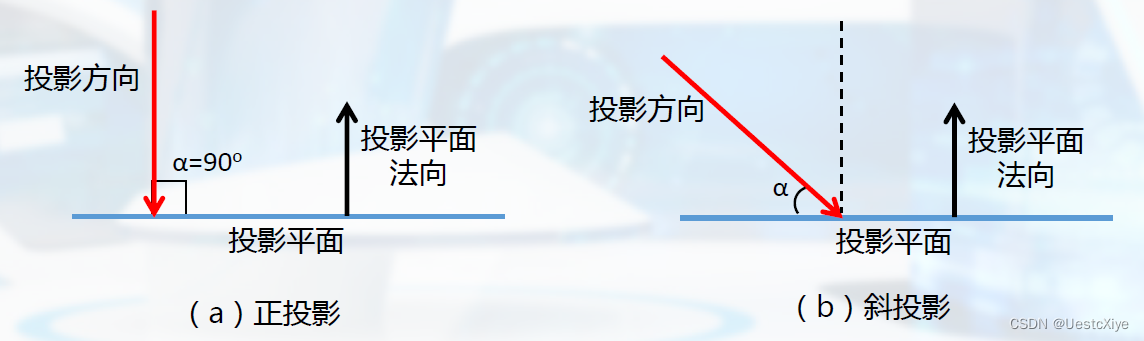
正投影
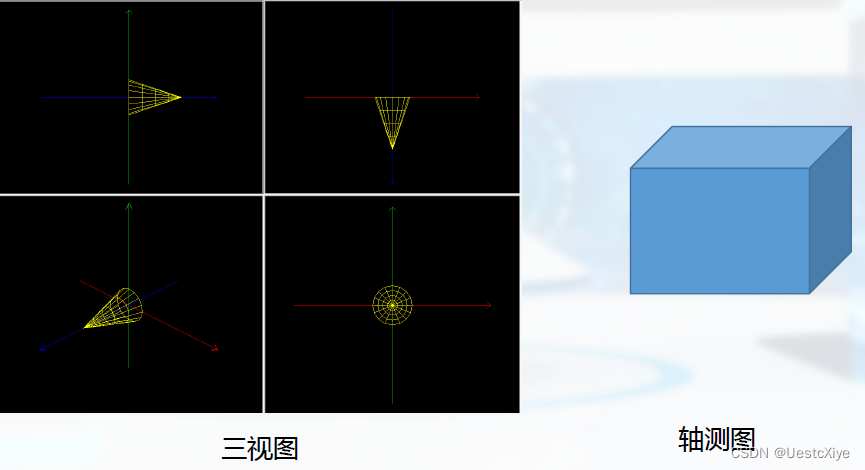
正投影分为:三视图、正轴测图。
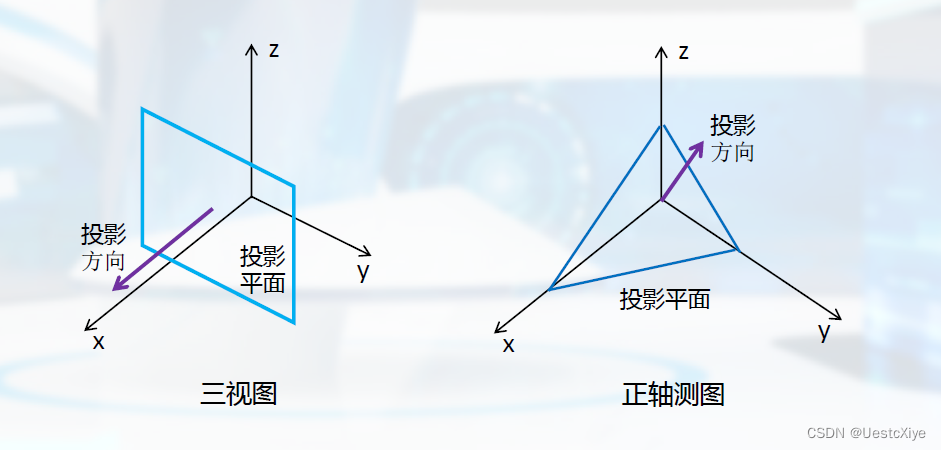
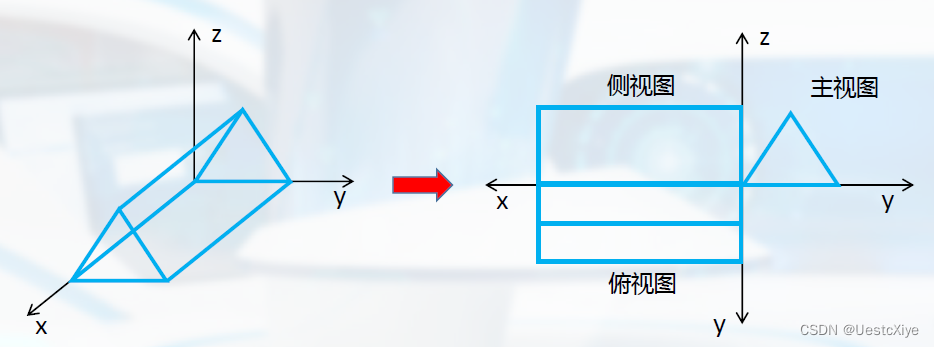
三视图:
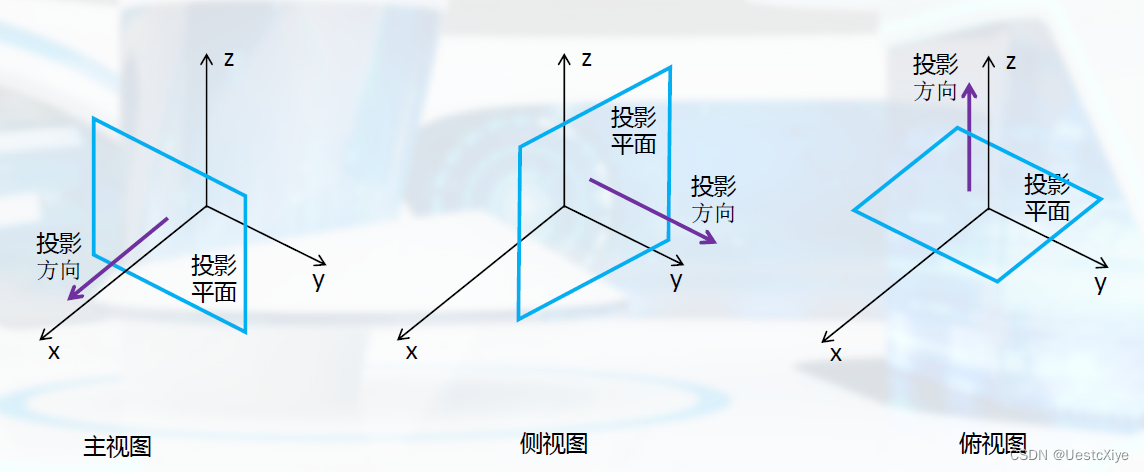
以投影面不x轴垂直,且在xp处的主视图为例:x’=xp,y’=y,z’=z。
轴测图:

当将该平面的法向量方向旋转到x轴,则投影平面为YOZ平面。
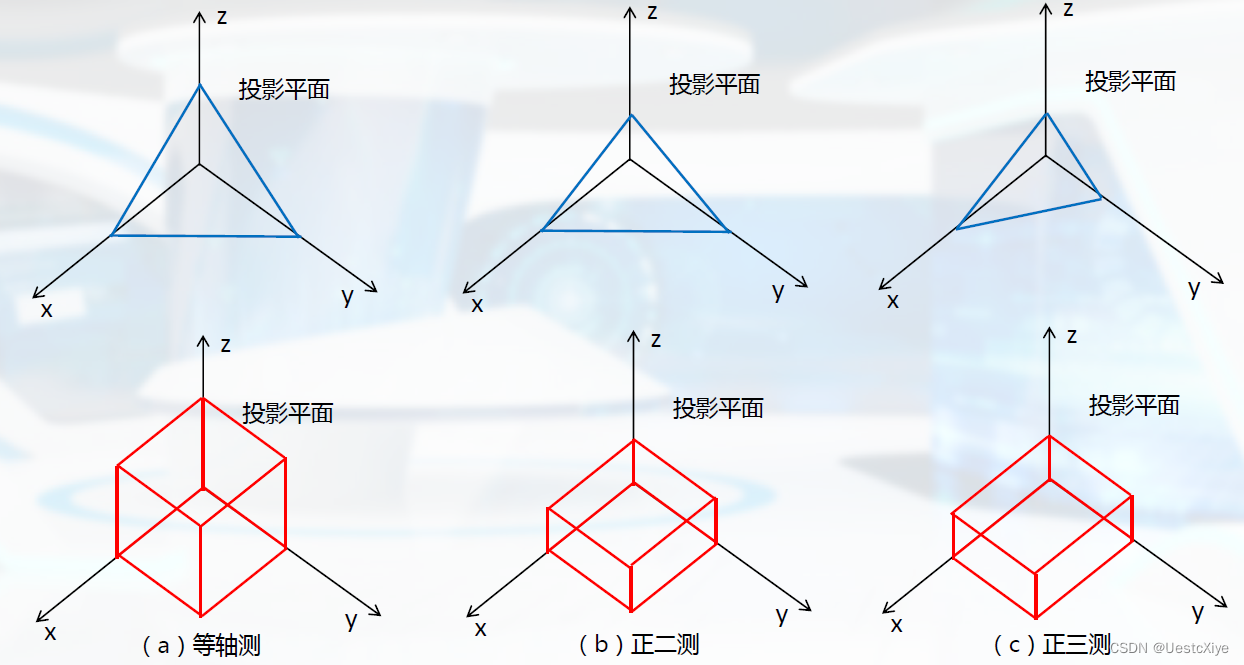
斜投影
常见的斜投影:斜等测和斜二测。
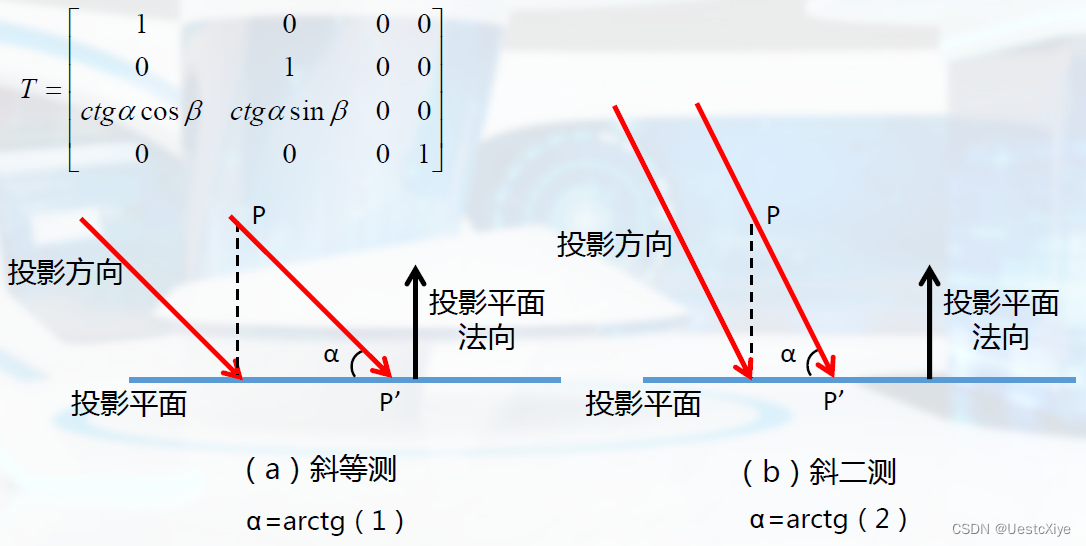
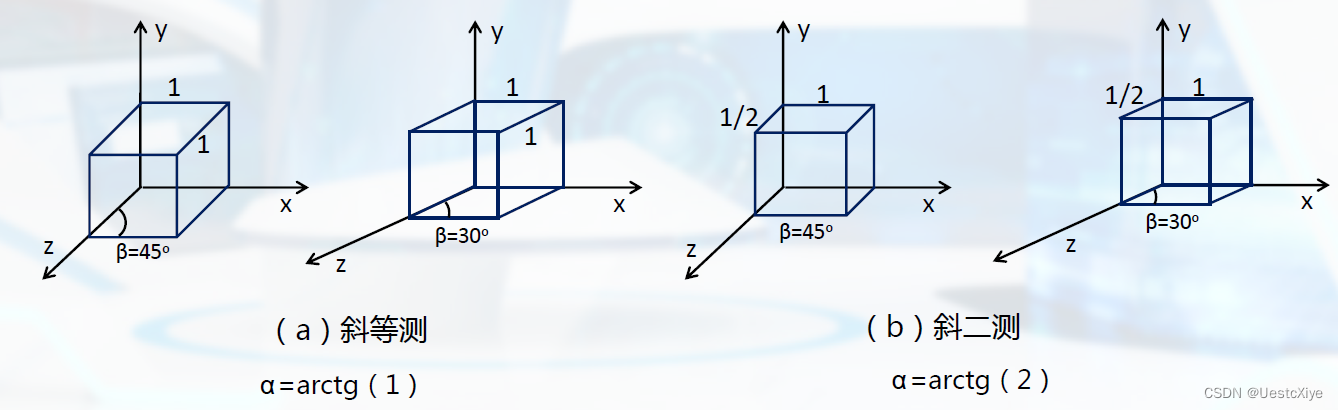
透视投影
基于三维齐次坐标的变换。
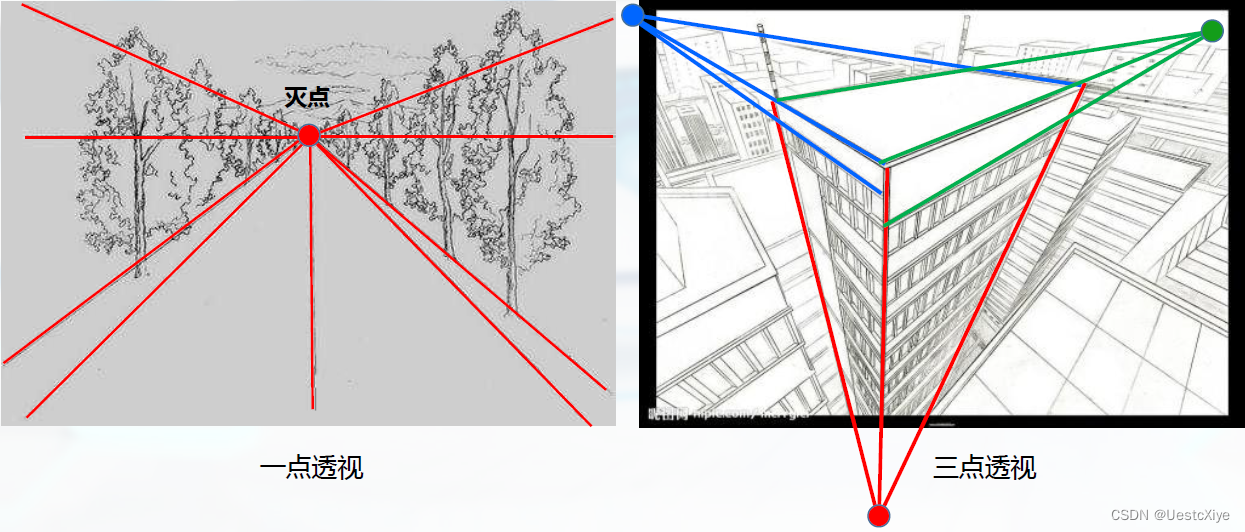
一点透视:
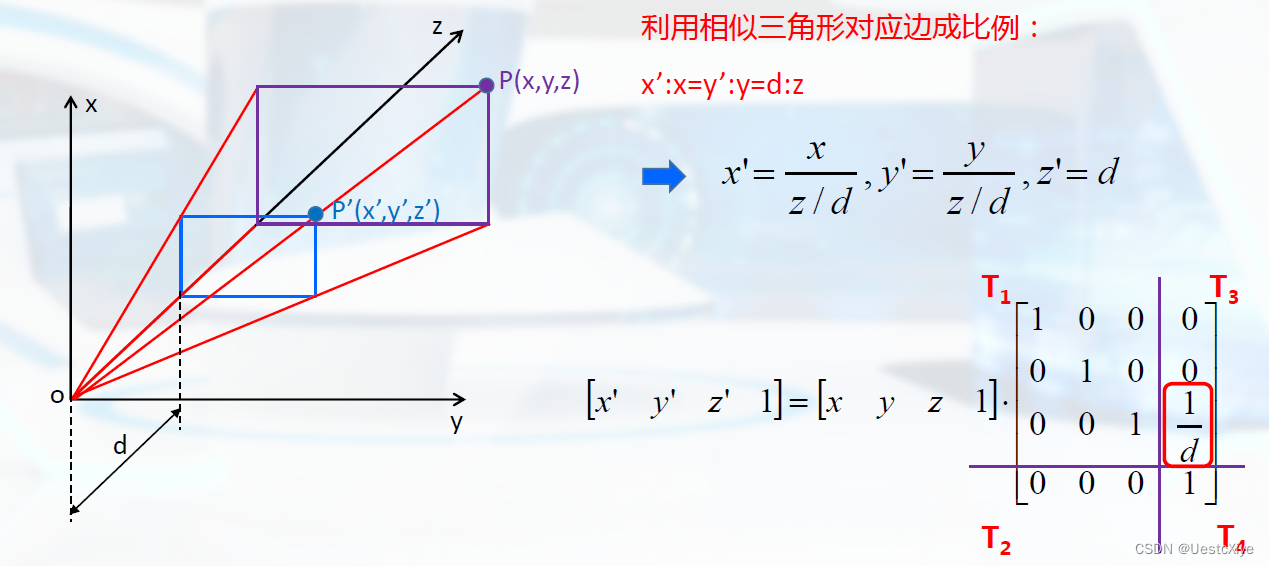
透视缩小效应:三维形体透视投影的大小不形体到投影中心的距离成反比。

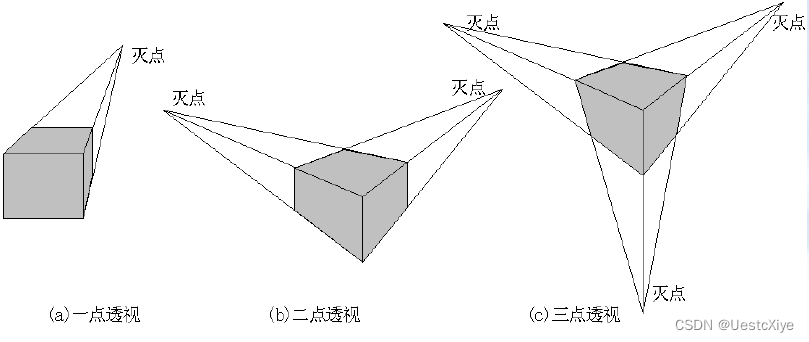
不平行于投影面的平行线的投影会汇聚到一个点,这个点称为灭点(VanishingPoint)。
坐标轴方向的平行线在投影面上形成的灭点称作主灭点。
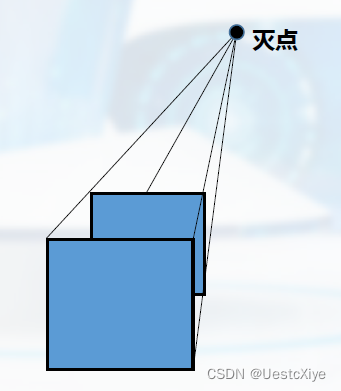
透视投影按照主灭点个数的分类:
- 一点透视有一个主灭点,即投影面不一个坐标轴正交,不另外两个坐标轴平行。
- 两点透视有两个主灭点,即投影面不两个坐标轴相交,不另一个坐标轴平行。
- 三点透视有三个主灭点,即投影面不三个坐标轴都相交。
7.2 规范化的投影变换
观察的要素
-
观察坐标系的位置:取决于视点的位置P、焦点的位置P0和向上的正方向yv。
-
观察方式:平行投影、透视投影。

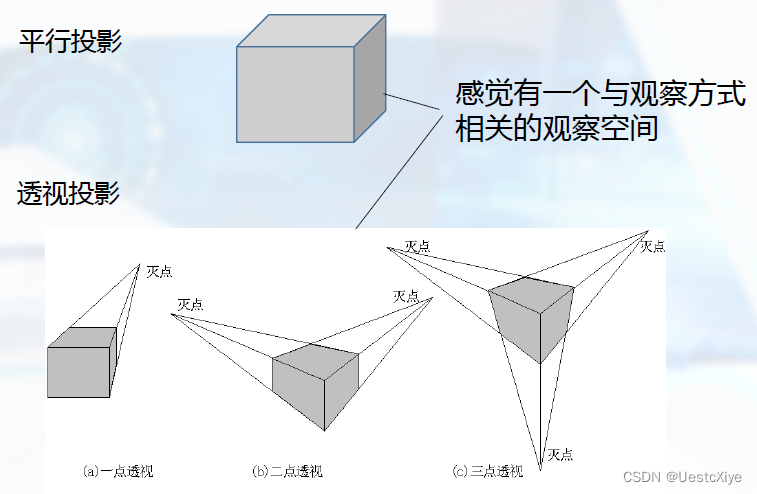
观察空间
观察窗口(ViewWindow),即观察平面上的一个有限区域。
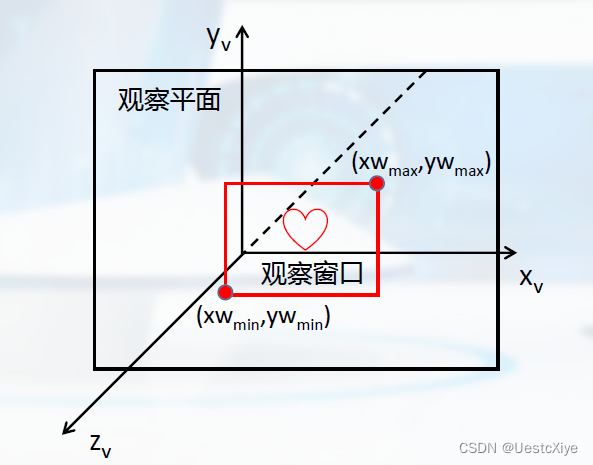
观察空间:定义了观察窗口后,可以利用窗口边界来定义观察空间。
将观察窗口沿zv轴方向作平移运动,产生的三维形体称为观察空间。

影响观察空间的要素:
- 观察窗口的大小
- 投影方式的不同
正平行投影的观察空间:

斜平行投影的观察空间:
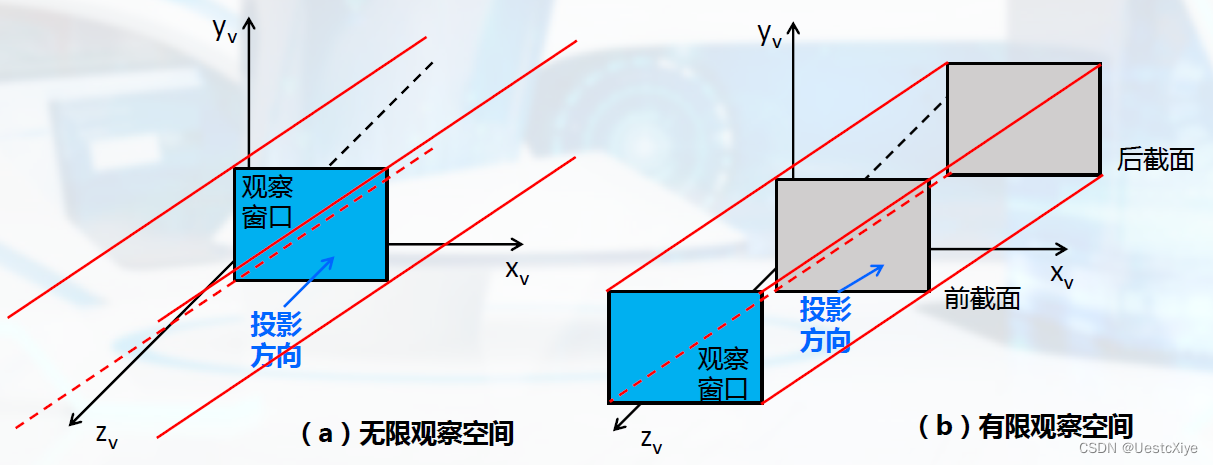
透视投影的观察空间:
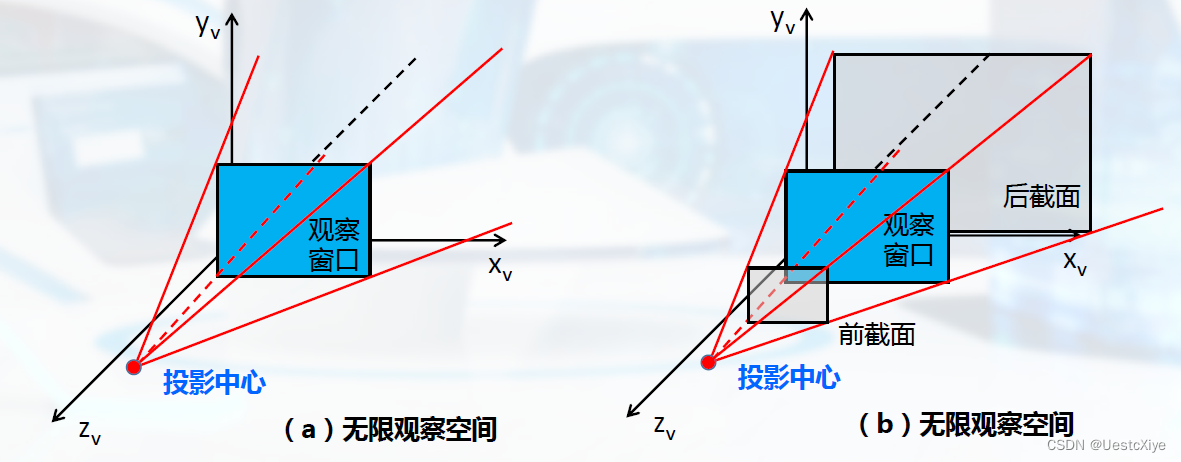
有限观察空间又称为裁剪空间,也叫视景体。
以下是丌同投影方式的视景体:
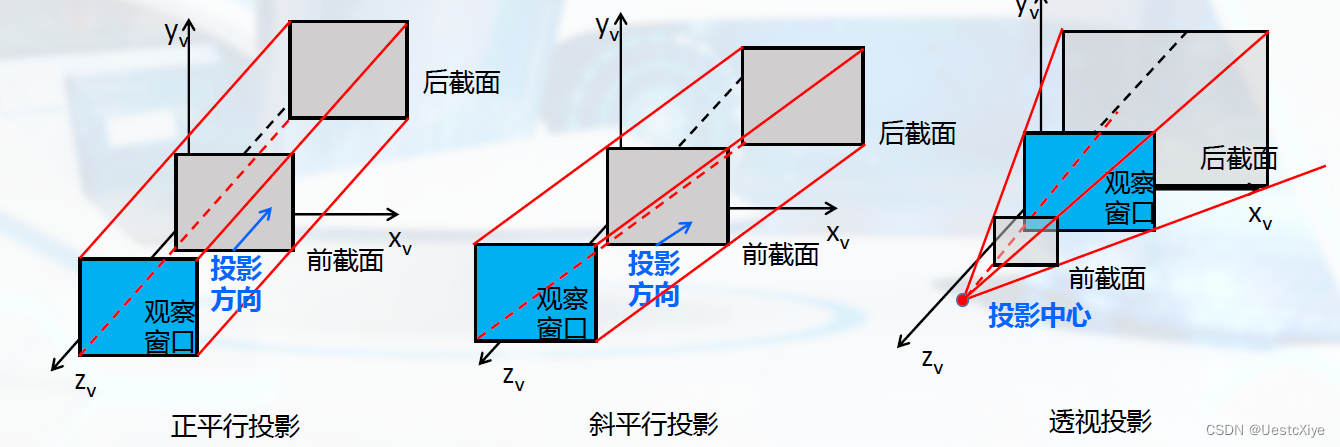
规范化的投影变换
几何阶段后续的工作:
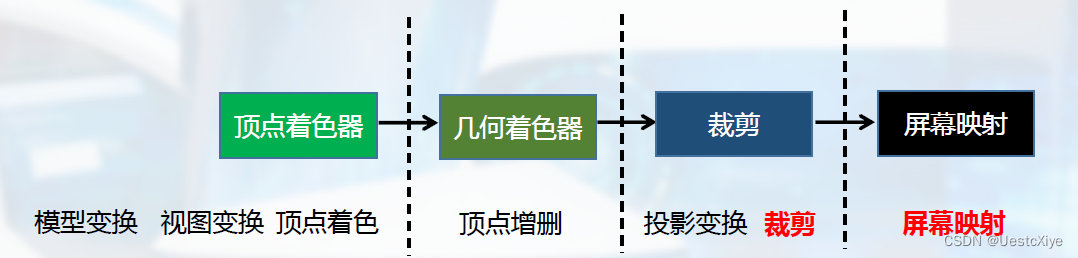
观察空间不同,裁剪和屏幕映射的方法不同。
能否有一个规范化的观察空间?
可以!
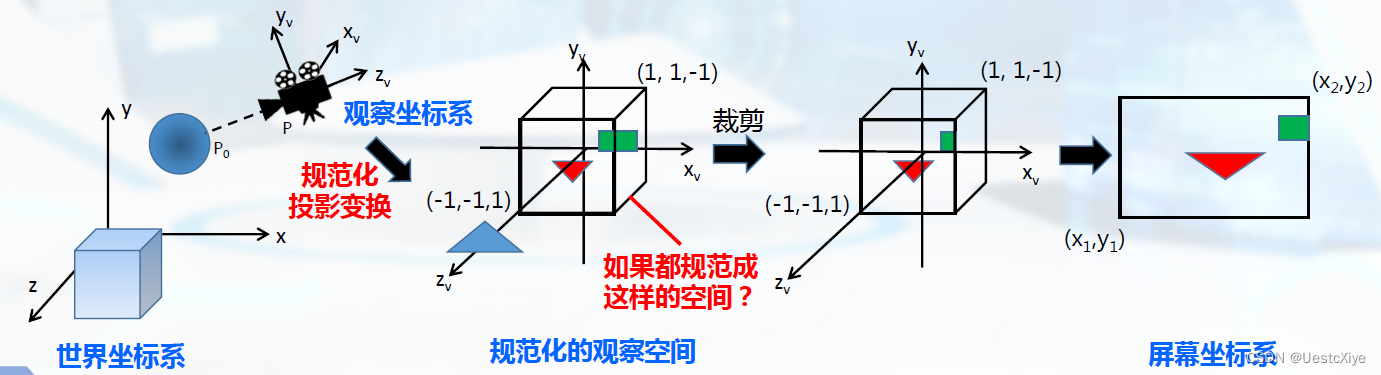
定义一个规范化投影空间:

怎么进行规范化投影变换?
首先考虑平行投影中最简单的正平行投影:平移和比例变化。
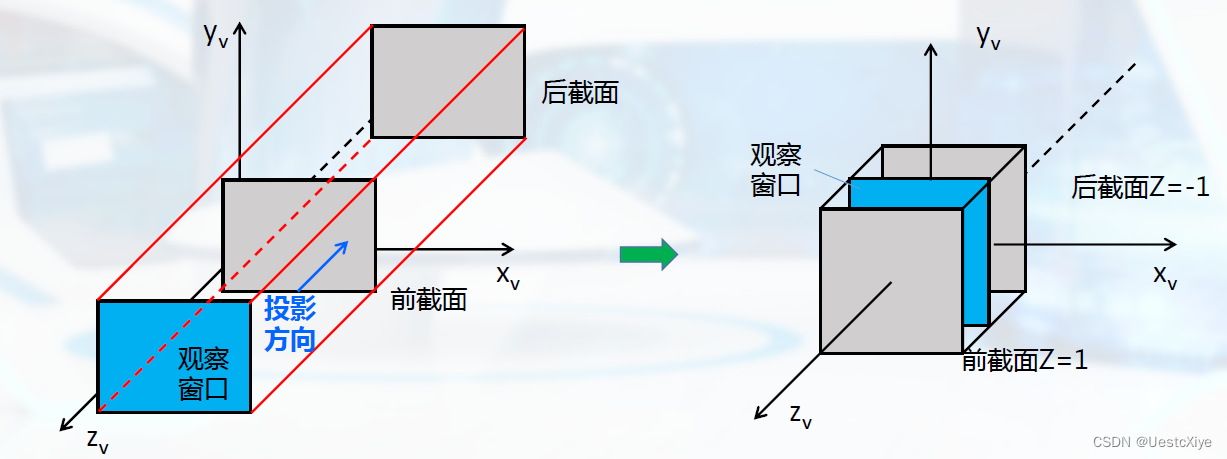
再看斜平行投影:平移和比例变化。
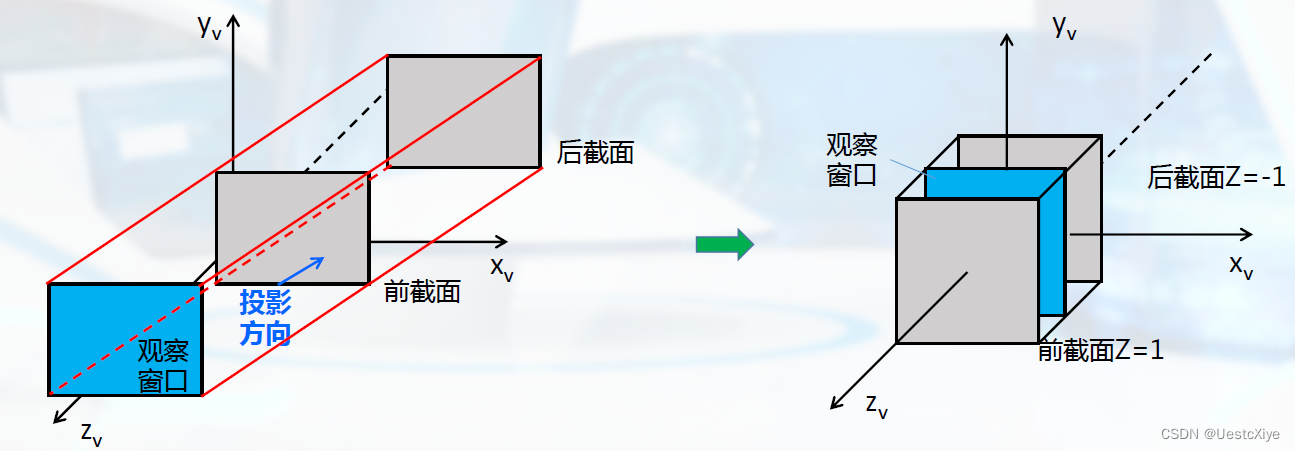
斜平行投影:错切、平移和比例变化。

透视投影:平移、比例和错切变化。
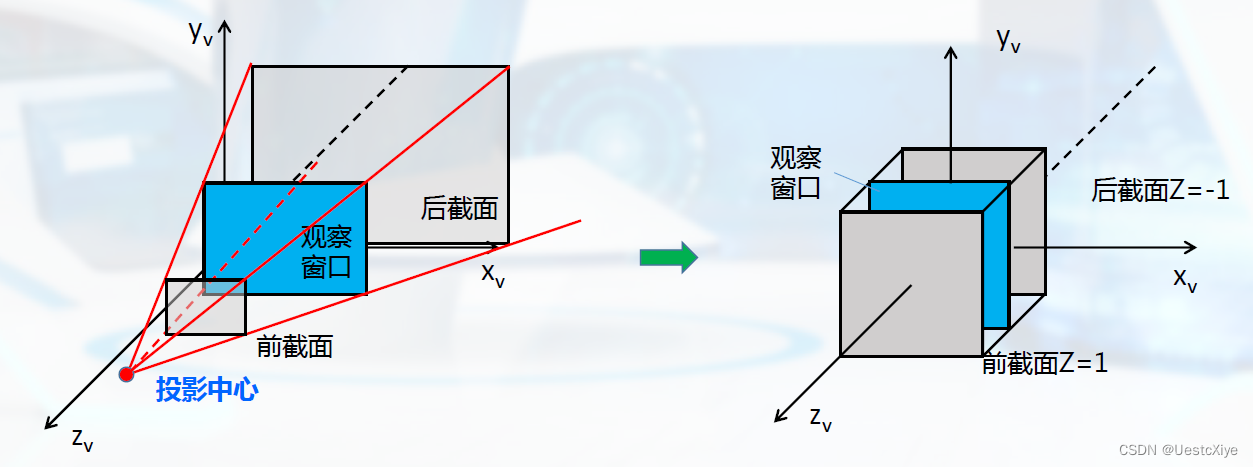
规范化投影空间的过程:矩阵运算
在OpenGL中,投影矩阵的计算只需要调用一个函数:
fovglm::mat4 proj =glm::perspective(45.0f, 1.3f, 0.1f, 100.0f);
- 第一个参数定义了fov的值,它表示的是视野(Field of View),并且设置了观察空间的大小。对于一个真实的观察效果,它的值经常设置为45.0,但想要看到更多结果你可以设置一个更大的值。
- 第二个参数设置了宽高比,就是宽度和高度的比例。
- 第三和第四个参数设置了近截面和远截面的位置。我们经常设置近距离为0.1而远距离设为100.0。所有在近平面和远平面的顶点且处于平截头体内的顶点都会被渲染。
规范化投影变换的目的:便于后续的裁剪和屏幕映射。