关于小波，Morlet，Grossmann，Meyer，Daubechies，Mallat

转自：未来数学家，向大佬致敬。

匈牙利电子工程师丹尼斯·加博尔（Dennis Gabor）1946年提出加窗傅里叶变换，开创了在时间-频率平面上分析信号的方法，Gabor还发明了全息摄影术，这项工作让他获得了1971年的诺贝尔物理学奖。

2017 阿贝尔奖得主迈耶及受邀报告人(从左至右)：马拉特、迈耶、多贝西、伊曼纽尔·坎德斯

在Gabor获诺奖的第二年，一位默默无闻的地球物理工程师让·莫莱（Jean Morlet），在法国一家石油公司从事了多年的野外工作后转入研发部，开始分析地震信号。他用加窗傅里叶变换分析信号得到的结果很差，发现原因是地震信号中有瞬间剧烈的波动，而加窗傅里叶变换中的窗函数不能自动适应这种变化。

Morlet于是构造出一个窗口宽度可以调节的复函数

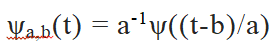
由

通过尺度参数 a 和平移参数 b 得到。当正数 a 很小时，函数窗口变窄，就能探测出信号的瞬间变化，Morlet因此创立了分析信号的时间-尺度方法。他把

叫做 “wavelets of constant shape”，这就是小波（wavelet）一词的由来，Morlet使用它建立了分解和重构信号的公式，发现比加窗傅里叶变换更有效。他先后于1975年和1980年在勘探地球物理学家协会主办的国际会议上做了报告，没有产生影响。不仅如此，他在发现小波变换后不久，竟被公司以提前退休的名义解聘，在50岁的时候失去了工作。他一度非常沮丧，但仍然继续为自己的发现寻找理论证明。1981年，Morlet联系母校巴黎综合理工学院的物理学家罗杰·巴利安（Roger Balian）寻求帮助。巴利安推荐他找马赛大学的理论物理学家亚历克斯·格罗斯曼（Alex Grossmann）。在这一年的12月，Morlet见到了Grossmann。

亚历克斯·格罗斯曼（Alex Grossmann, 1930-2019）

Grossmann正是英格丽·多贝西（Ingrid Daubechies）的博士论文导师，Daubechies1975年在比利时布鲁塞尔自由大学获得物理学士学位后，继续攻读博士学位。名义上让·雷尼尔（Jean Reignier）是她的导师，她又根据自己的兴趣选择了马赛大学的Grossmann作为论文导师，研究方向是数学物理。

Grossmann是克罗地亚人，在1966年加入马赛大学后一直在那里工作。他同情Morlet的遭遇，也理解了他的想法，意识到Morlet的发现与量子力学中的相干态非常相似，他从群论的观点出发证明了解析小波在满足容许性条件下，可以由连续小波变换完美重构原始信号。容许性条件使得小波函数具有震荡和迅速衰减的形状，Morlet小波不是解析小波，但是产生的误差并不显著，所以能得到很好的结果。

他们合作的文章1984年发表在 SIAM 数学分析杂志上，成为连续小波变换的重要文献，在此后的数年里，两人在小波领域合作发表了十多篇论文。

（1991年）格罗斯曼(左)和莫莱(右)

1985年是Daubechies在布鲁塞尔自由大学理论物理系工作的第五个年头。五年前，她完成博士论文《量子力学算子的解析函数希尔伯特空间核表示》后留下来做研究助理，期间去贝尔实验室做了两年博士后。她在数学物理领域已经发表了20多篇论文，工作职位也从研究助理升为研究型教授。这一年的春天，她来到马赛访问Grossmann，被他在小波变换上的热情所感染。她发现自己掌握的数学工具恰好能用到信号分析中，感到兴奋不已，于是转向了小波研究。

就在多贝西到访前的一月，伊夫·迈耶（Yves Meyer），巴黎综合理工学院的一位数学家，访问了格罗斯曼。他有一次排队等候复印时，偶然从旁人的谈话中听到了格罗斯曼的工作。他从同事那里得到了论文的预印本。迈耶后来回忆说，“他们的论文深深地吸引了我，以至于我迫不及待地来到马赛。在和Grossmann一起讨论了三天后，我变成了他的学徒。”

伊夫·迈耶（Yves Meyer）

Meyer是分析学家，此前在卡尔德隆猜想上研究多年，他发现Morlet和Grossmann的工作实际上是对数学家艾尔伯特·卡尔德隆（Alberto Calderón）在1960年代末发现的卡尔德隆等式（Calderón‘s identity ）的再发现，使用卡尔德隆的方法可以把格罗斯曼和莫莱的工作从一维推广到高维。

在Meyer之前，小波的思想已经以不同的形式隐藏在数学、物理和信号处理等领域中。然而，正是他们—一位地球物理工程师和一位理论物理学家—以新的形式再次独立发现，开启了小波革命。

Grossmann建议Daubechies研究离散小波变换，也就是寻找一族小波函数分解和重构信号。他们和Meyer合作，在9月完成了L2(R) 空间小波框架的构建。与空间中的基相比，框架是有冗余的。例如在平面 R2上，(0, 1) 和 (1, 0) 构成一个标准正交基，而 (0, 1) 、(-√3/2, -1/2) 和 (√3/2, -1/2) 是一个框架。

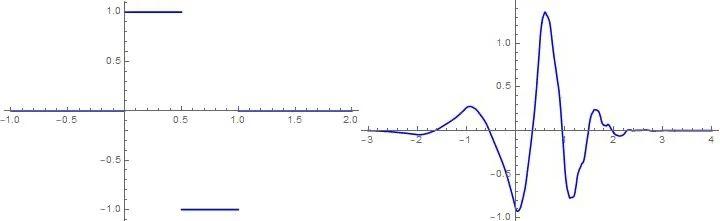
与此同时，Meyer开始寻找希尔伯特空间 L2(R) 中的小波标准正交基。早在1909年，希尔伯特的学生、匈牙利数学家哈尔（Alfréd Haar）在博士论文中构造了一组标准正交基，由一个分片常函数通过平移和放缩得到。它恰好是一组小波标准正交基，现在叫做Haar小波，Haar小波是不连续的，更不光滑。Meyer没有意识到斯特伦贝格（J. O. Strömberg）在1981年使用样条函数构造了C^k光滑的小波标准正交基，猜测不存在光滑小波标准正交基，但在试图证明的过程中，却构造出了一个无穷光滑的小波标准正交基，现在叫做Meyer小波。

Meyer小波以及后来的威尔逊-多贝西变换为引力波的发现立了大功。

“他们发现引力波的那天，给我发了一封电子邮件，说我的工作是发现它的基础”，Meyer在2017年获得阿贝尔奖后接受采访时说。"当你的工作被应用到如此辉煌的发现时，那真是令人兴奋！"

在研究小波前，Meyer在卡尔德隆猜想上工作了七年，发现Meyer小波只花了三个月的时间。Meyer小波

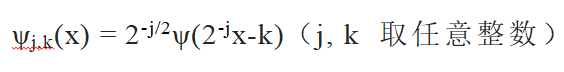
是一个二进小波，即它的尺度以 2^j 的形式改变。ψ(x) 是一个无穷光滑的实带限函数，在频率域有紧支集，但在时间域支集（由函数不等于0的点组成的集合的闭集）是无穷大，所以在应用中通常使用Meyer小波的傅里叶变换。

1986年的11月，Meyer受邀到芝加哥大学做报告，碰到了从宾夕法尼亚大学赶来的斯蒂芬·马拉特（Stéphane Mallat），Mallat也是法国人，从巴黎综合理工学院毕业后，在宾大计算机与信息科学系读博士，研究领域是图像分析。

斯蒂芬·马拉特（Stéphane Mallat ）

Mallat碰巧有一位大学同学是Meyer的研究生，在暑假期间从他那里偶然得知了Meyer小波。他很快有了新发现：标准正交小波基的构造与图像处理中的拉普拉斯金字塔算法非常相似，后者把图像从细到粗进行分解，形成一个金字塔状。他尝试着把这种多分辨的思想植入到标准正交小波基的构造中。当得知Meyer要去芝加哥大学时，他带着自己的想法专程赶来。

这一次，在赞格蒙（Antoni Zygmund）教授的办公室里，Meyer和Mallat讨论了三天，建立了 L2(R) 空间中构造标准正交小波基的多分辨分析理论。

Mallat带着讨论的成果回去后，又构造出了用离散小波变换分解和重构图像的快速算法，可以把图像从细到粗分解成多个尺度，再快速地重构。他把这些进展整理成论文。

第二年初Daubechies收到了Mallat寄来的小波多分辨分析的预印本。她最近在小波框架上又完成了一项大工作，开始考虑标准正交小波基的构造。她在多分辨分析下研究Meyer小波发现，它的滤波器无限长（有无穷多非零值），要应用到离散信号中只能截取有限个部分。Daubechies的想法是，先不考虑多分辨分析，能否直接构造出有限长度的滤波器，并且能够使用Mallat的分解和重构算法处理离散信号？如果这一步可行，观察对滤波器再加入什么条件，就可以由它们在多分辨分析下得到紧支撑的标准正交小波基。

英格丽·多贝西（Ingrid Daubechies）

沿着这个思路，Daubechies给出了构造光滑紧支撑小波标准正交基的理论和方法，Daubechies小波诞生了，根据她的分析，只要满足条件的滤波器是有限长的，得到的标准正交小波基就是紧支撑的。并且，滤波器的长度越长，得到的Daubechies小波越光滑。例如滤波器最短的Daubechies小波就是不光滑的哈尔小波，而由一个由长度为8的滤波器得到Daubechies小波（db4）就光滑了许多。