经典图割算法中图的:Graph-Cut
- 一.graph-cut:准则函数
- 二.Graph-cut:图的建立
- 1.术语:
- 2.图的建立
- 3. 头文件
- 4. 源文件
- 5. 测试图像
讲解目前典型的3种图割算法:graph-cut、grab-but、one-cut。本文主要讲解graph-cut的方法在应用时,准则函数与图构建关系,如何构建图,以及如何代码实现图的构建。图割的原理网上文章和论文已介绍比较详细,不再详细介绍。
一.graph-cut:准则函数
该方法可谓是图割方法的开山鼻祖。该方法的准则函数如下:
E ( A ) = λ R ( A ) + B ( A ) E(A) = \lambda R(A) + B(A) E(A)=λR(A)+B(A)
R(A)是先验惩罚项,B(A)是区域相似度惩罚项, λ \lambda λ是平衡因子。
该准则函数意义:同类间,颜色差别小;异类间,颜色差别大。原则上该准则可解决图像任意类分割,并且一定是有全局最优解得,但在无种子点的超过2分类的问题时,该优化是个NP难问题,需要进行指数级的比较才能获得最优解,无工程价值。
二.Graph-cut:图的建立
1.术语:
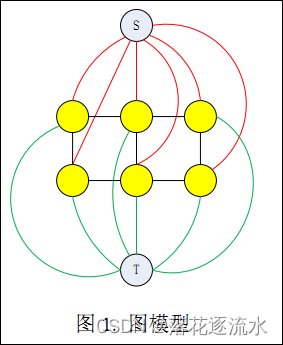
- 与S和T链接的边叫t-link(红线与绿线),领域之间的链接边叫n-link(黑线)。其中红线进一步称为s-t-link,绿线进一步称为t-t-link。
- 黑线的权值对应的是B(A)项,红线与绿线的权值对应的是R(A)项。
- 权值用w表示。
- 蓝色节点表示类别标志节点,S表示正类类标节点,T表示负类类标节点,黄色节点是图像中的每一个像素点。
最终通过求最小割之后,与节点S相连的所有黄色节点(图像像素点)属于一类,同理与节点T相连的所有黄色节点属于另一类。两类被最小割割开,割值即是准则函数的值。
2.图的建立
拿到待分割的图像后,图的节点与边已确定,即图的形状已确定下来。仅仅需要做的就是给图中所有边赋值相应的权值。
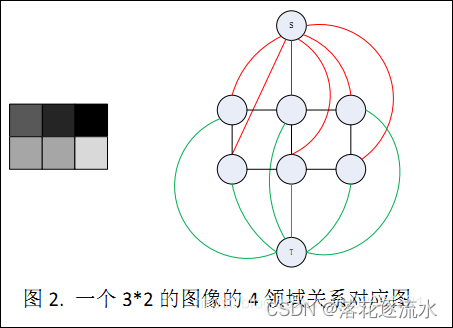
图中的边有3种情况:种子点的t-link;非种子点的t-link;像素领域关系的n-link。接下来将说明每一种边的权值取值。
1).种子点t-link权值:种子点认为是硬约束,其用户预设类别后,类别不会随分割算法而改变。
a.对于正类别种子点,s-t-link必须保留,t-t-link必须割去。工程中,通过将s-t-link权值设置为超级大值,t-t-link设置为0。保证一定仅仅割去t-t-link,否则一定不是最小割,因为当前w(s-t-link)权值是超级大值,割去这条边的代价一定是最大的。
b.反之同理。
2).非种子点的t-link权值:通过正负类种子点,我们能建立2类的颜色直方图。将直方图归一化成概率密度函数,定义为H_F,H_B。其中s-t-link权值为-ln(H_F(x)),t-t-link权值为-ln(H_B(x)),x为该像素点颜色值。
3).n-link权值:n-link用于度量相邻像素点之间颜色的差异性。设一对相邻点Pi,Pj,则n-link(Pi-Pj)的权值w等于:
w = exp ( − ( x i − x j ) 2 2 σ 2 ) ⋅ 1 d i s t ( P i , P j ) w = \exp(-\frac{(x_i - x_j)^2}{2\sigma^2}) \cdot \frac{1}{dist(P_i,P_j)} w=exp(−2σ2(xi−xj)2)⋅dist(Pi,Pj)1
其中,dist()是距离函数,表示点之间的图像距离。即4领域下,所以领域点距离均为1,;8领域下,对角像素点距离为 2 \sqrt{2} 2;在5*5领域下,对角像素点距离为 2 2 2\sqrt{2} 22。
设种子点的超级大值是1000,
σ
=
1
\sigma = 1
σ=1。图像是3*2的灰度图,数字表示灰度值,红色和蓝色节点表示用户选择的正负种子点。当然种子点过少时,计算的H_F,H_B可能不准,可将种子点附近的像素点也算入先验直方图中,往往可以取得更好效果。
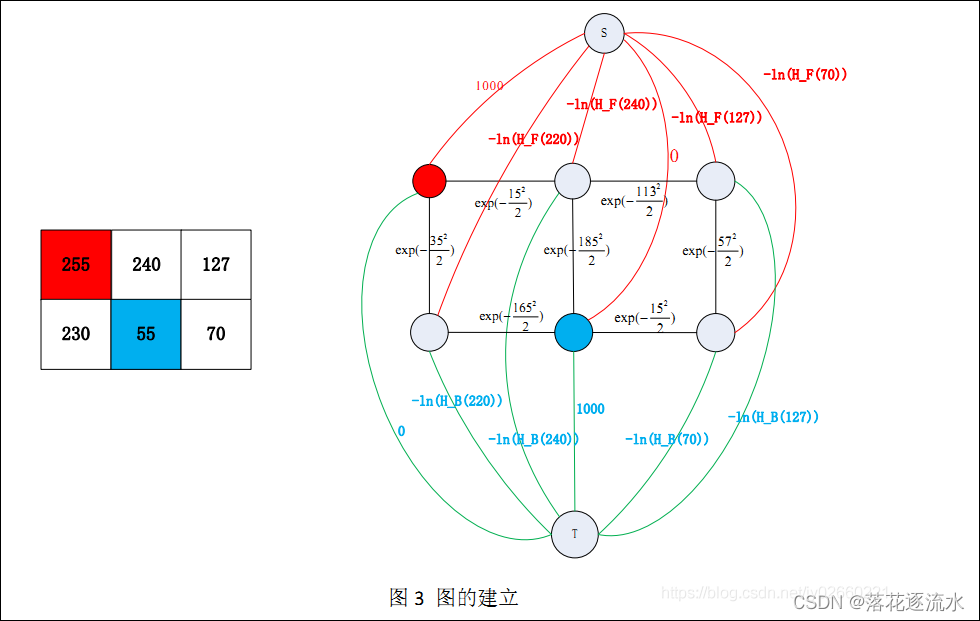
如上图所示,将所有边的权值赋值后,图就建立完毕。剩余则直接运用最小割算法即可求解。最小割算法有很多,包括graph-cut作者提出的快速算法An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision。Opencv即采用该算法计算最小割。
代码适配了opencv4.6.0
3. 头文件
gcgraphMy.h
#include <vector>
#include <assert.h>
using namespace std;
#define MIN(a,b) (((a)<(b))?(a):(b))
typedef unsigned char uchar;
template <class TWeight>
class GCGraphMy
{
public:
GCGraphMy();
GCGraphMy(unsigned int vtxCount, unsigned int edgeCount);
~GCGraphMy();
void create(unsigned int vtxCount, unsigned int edgeCount); //给图的结点容器和边容器分配内存
int addVtx(); //添加空结点
void addEdges(int i, int j, TWeight w, TWeight revw); //添加点之间的边n-link
void addTermWeights(int i, TWeight sourceW, TWeight sinkW); //添加结点到顶点的边t-link
TWeight maxFlow(); //最大流函数
bool inSourceSegment(int i); //图对象调用最大流函数后,判断结点属不属于属于源点类(前景)
private:
class Vtx //结点类
{
public:
Vtx *next; //在maxflow算法中用于构建先进-先出队列
int parent;
int first; //首个相邻边
int ts; //时间戳
int dist; //到树根的距离
TWeight weight;
uchar t; //图中结点的标签,取值0或1,0为源节点(前景点),1为汇节点(背景点)
};
class Edge //边类
{
public:
int dst; //边指向的结点
int next; //该边的顶点的下一条边
TWeight weight; //边的权重
};
std::vector<Vtx> vtcs; //存放所有的结点
std::vector<Edge> edges; //存放所有的边
TWeight flow; //图的流量
};
template <class TWeight>
GCGraphMy<TWeight>::GCGraphMy()
{
flow = 0;
}
template <class TWeight>
GCGraphMy<TWeight>::GCGraphMy(unsigned int vtxCount, unsigned int edgeCount)
{
create(vtxCount, edgeCount);
}
template <class TWeight>
GCGraphMy<TWeight>::~GCGraphMy()
{
}
template <class TWeight>
void GCGraphMy<TWeight>::create(unsigned int vtxCount, unsigned int edgeCount) //构造函数的实际内容,根据节点数和边数
{
vtcs.reserve(vtxCount);
edges.reserve(edgeCount + 2);
flow = 0;
}
/*
函数功能:添加一个空结点,所有成员初始化为空
参数说明:无
返回值:当前结点在集合中的编号
*/
template <class TWeight>
int GCGraphMy<TWeight>::addVtx()
{
Vtx v;
memset(&v, 0, sizeof(Vtx)); //将结点申请到的内存空间全部清0(第二个参数0) 目的:由于结点中存在成员变量为指针,指针设置为null保证安全
v.first = -1;
vtcs.push_back(v);
return (int)vtcs.size() - 1; //返回值:当前结点在集合中的编号
}
/*
函数功能:添加一条结点i和结点j之间的边n-link(普通结点之间的边)
参数说明:
int---i: 弧头结点编号
int---j: 弧尾结点编号
Tweight---w: 正向弧权值
Tweight---reww: 逆向弧权值
返回值:无
*/
template <class TWeight>
void GCGraphMy<TWeight>::addEdges(int i, int j, TWeight w, TWeight revw)
{
assert(i >= 0 && i < (int)vtcs.size());
assert(j >= 0 && j < (int)vtcs.size());
assert(w >= 0 && revw >= 0);
assert(i != j);
Edge fromI, toI; // 正向弧:fromI, 反向弧 toI
fromI.dst = j; // 正向弧指向结点j
fromI.next = vtcs[i].first; //每个结点所发出的全部n-link弧0(4个方向)都会被连接为一个链表,采用头插法插入所有的弧
fromI.weight = w; // 正向弧的权值w
vtcs[i].first = (int)edges.size(); //修改结点i的第一个弧为当前正向弧
edges.push_back(fromI); //正向弧加入弧集合
toI.dst = i;
toI.next = vtcs[j].first;
toI.weight = revw;
vtcs[j].first = (int)edges.size();
edges.push_back(toI);
}
/*
函数功能:为结点i的添加一条t-link弧(到终端结点的弧),添加节点的时候,同时调用此函数
参数说明:
int---i: 结点编号
Tweight---sourceW: 正向弧权值
Tweight---sinkW: 逆向弧权值
返回值:无
*/
template <class TWeight>
void GCGraphMy<TWeight>::addTermWeights(int i, TWeight sourceW, TWeight sinkW)
{
assert(i >= 0 && i < (int)vtcs.size());
TWeight dw = vtcs[i].weight;
if (dw > 0)
sourceW += dw;
else
sinkW -= dw;
flow += (sourceW < sinkW) ? sourceW : sinkW;
vtcs[i].weight = sourceW - sinkW;
}
/*
函数功能:最大流函数,将图的所有结点分割为源点类(前景)还是汇点类(背景)
参数:无
返回值:图的成员变量--flow
*/
template <class TWeight>
TWeight GCGraphMy<TWeight>::maxFlow()
{
const int TERMINAL = -1, ORPHAN = -2;
Vtx stub, *nilNode = &stub, *first = nilNode, *last = nilNode;//先进先出队列,保存当前活动结点,stub为哨兵结点
int curr_ts = 0; //当前时间戳
stub.next = nilNode; //初始化活动结点队列,首结点指向自己
Vtx *vtxPtr = &vtcs[0]; //结点l指针
Edge *edgePtr = &edges[0]; //弧指针
vector<Vtx*> orphans; //孤立点集合
// 遍历所有的结点,初始化活动结点(active node)队列
for (int i = 0; i < (int)vtcs.size(); i++)
{
Vtx* v = vtxPtr + i;
v->ts = 0;
if (v->weight != 0) //当前结点t-vaule(即流量)不为0
{
last = last->next = v; //入队,插入到队尾
v->dist = 1; //路径长度记1
v->parent = TERMINAL; //标注其双亲为终端结点
v->t = v->weight < 0;
}
else
v->parent = 0; //孤结点
}
first = first->next; //首结点作为哨兵使用,本身无实际意义,移动到下一节点,即第一个有效结点
last->next = nilNode; //哨兵放置到队尾了。。。检测到哨兵说明一层查找结束
nilNode->next = 0;
//很长的循环,每次都按照以下三个步骤运行:
//搜索路径->拆分为森林->树的重构
for (;;)
{
Vtx* v, *u; // v表示当前元素,u为其相邻元素
int e0 = -1, ei = 0, ej = 0;
TWeight minWeight, weight; // 路径最小割(流量), weight当前流量
uchar vt; // 流向标识符,正向为0,反向为1
//---------------------------- 第一阶段: S 和 T 树的生长,找到一条s->t的路径 -------------------------//
while (first != nilNode)
{
v = first; // 取第一个元素存入v,作为当前结点
if (v->parent) // v非孤儿点
{
vt = v->t; // 纪录v的流向
// 广度优先搜索,以此搜索当前结点所有相邻结点, 方法为:遍历所有相邻边,调出边的终点就是相邻结点
for (ei = v->first; ei != -1; ei = edgePtr[ei].next)
{
// 每对结点都拥有两个反向的边,ei^vt表明检测的边是与v结点同向的
if (edgePtr[ei^vt].weight == 0)
continue;
u = vtxPtr + edgePtr[ei].dst; // 取出邻接点u
if (!u->parent) // 无父节点,即为孤儿点,v接受u作为其子节点
{
u->t = vt; // 设置结点u与v的流向相同
u->parent = ei ^ 1; // ei的末尾取反。。。
u->ts = v->ts; // 更新时间戳,由于u的路径长度通过v计算得到,因此有效性相同
u->dist = v->dist + 1; // u深度等于v加1
if (!u->next) // u不在队列中,入队,插入位置为队尾
{
u->next = nilNode; // 修改下一元素指针指向哨兵
last = last->next = u; // 插入队尾
}
continue;
}
if (u->t != vt) // u和v的流向不同,u可以到达另一终点,则找到一条路径
{
e0 = ei ^ vt;
break;
}
// u已经存在父节点,但是如果u的路径长度大于v+1,且u的时间戳较早,说明u走弯路了,修改u的路径,使其成为v的子结点
if (u->dist > v->dist + 1 && u->ts <= v->ts)
{
// reassign the parent
u->parent = ei ^ 1; // 从新设置u的父节点为v(编号ei),记录为当前的弧
u->ts = v->ts; // 更新u的时间戳与v相同
u->dist = v->dist + 1; // u为v的子结点,路径长度加1
}
}
if (e0 >= 0)
break;
}
// exclude the vertex from the active list
first = first->next;
v->next = 0;
}
if (e0 < 0)
break;
//----------------------------------- 第二阶段: 流量统计与树的拆分 ---------------------------------------//
//第一节: 查找路径中的最小权值
minWeight = edgePtr[e0].weight;
assert(minWeight > 0);
// 遍历整条路径分两个方向进行,从当前结点开始,向前回溯s树,向后回溯t树
// 2次遍历, k=1: 回溯s树, k=0: 回溯t树
for (int k = 1; k >= 0; k--)
{
//回溯的方法为:取当前结点的父节点,判断是否为终端结点
for (v = vtxPtr + edgePtr[e0^k].dst;; v = vtxPtr + edgePtr[ei].dst)
{
if ((ei = v->parent) < 0)
break;
weight = edgePtr[ei^k].weight;
minWeight = MIN(minWeight, weight);
assert(minWeight > 0);
}
weight = fabs((float)v->weight);
minWeight = MIN(minWeight, weight);
assert(minWeight > 0);
}
/*第二节:修改当前路径中的所有的weight权值
任何时候s和t树的结点都只有一条边使其连接到树中,当这条弧权值减少为0则此结点从树中断开,
若其无子结点,则成为孤立点,若其拥有子结点,则独立为森林,但是ei的子结点还不知道他们被孤立了!
*/
edgePtr[e0].weight -= minWeight; //正向路径权值减少
edgePtr[e0 ^ 1].weight += minWeight; //反向路径权值增加
flow += minWeight; //修改当前流量
// k = 1: source tree, k = 0: destination tree
for (int k = 1; k >= 0; k--)
{
for (v = vtxPtr + edgePtr[e0^k].dst;; v = vtxPtr + edgePtr[ei].dst)
{
if ((ei = v->parent) < 0)
break;
edgePtr[ei ^ (k ^ 1)].weight += minWeight;
if ((edgePtr[ei^k].weight -= minWeight) == 0)
{
orphans.push_back(v);
v->parent = ORPHAN;
}
}
v->weight = v->weight + minWeight*(1 - k * 2);
if (v->weight == 0)
{
orphans.push_back(v);
v->parent = ORPHAN;
}
}
//---------------------------- 第三阶段: 树的重构 寻找新的父节点,恢复搜索树 -----------------------------//
curr_ts++;
while (!orphans.empty())
{
Vtx* v = orphans.back(); //取一个孤儿
orphans.pop_back(); //删除栈顶元素,两步操作等价于出栈
int d, minDist = INT_MAX;
e0 = 0;
vt = v->t;
// 遍历当前结点的相邻点,ei为当前弧的编号
for (ei = v->first; ei >= 0; ei = edgePtr[ei].next)
{
if (edgePtr[ei ^ (vt ^ 1)].weight == 0)
continue;
u = vtxPtr + edgePtr[ei].dst;
if (u->t != vt || u->parent == 0)
continue;
// 计算当前点路径长度
for (d = 0;;)
{
if (u->ts == curr_ts)
{
d += u->dist;
break;
}
ej = u->parent;
d++;
if (ej < 0)
{
if (ej == ORPHAN)
d = INT_MAX - 1;
else
{
u->ts = curr_ts;
u->dist = 1;
}
break;
}
u = vtxPtr + edgePtr[ej].dst;
}
// update the distance
if (++d < INT_MAX)
{
if (d < minDist)
{
minDist = d;
e0 = ei;
}
for (u = vtxPtr + edgePtr[ei].dst; u->ts != curr_ts; u = vtxPtr + edgePtr[u->parent].dst)
{
u->ts = curr_ts;
u->dist = --d;
}
}
}
if ((v->parent = e0) > 0)
{
v->ts = curr_ts;
v->dist = minDist;
continue;
}
/* no parent is found */
v->ts = 0;
for (ei = v->first; ei >= 0; ei = edgePtr[ei].next)
{
u = vtxPtr + edgePtr[ei].dst;
ej = u->parent;
if (u->t != vt || !ej)
continue;
if (edgePtr[ei ^ (vt ^ 1)].weight && !u->next)
{
u->next = nilNode;
last = last->next = u;
}
if (ej > 0 && vtxPtr + edgePtr[ej].dst == v)
{
orphans.push_back(u);
u->parent = ORPHAN;
}
}
}
//第三阶段结束
}
return flow; //返回最大流量
}
/*
函数功能:判断结点是不是源点类(前景)
参数:结点在容器中位置
返回值:1或0,1:结点为前景,0:结点为背景
*/
template <class TWeight>
bool GCGraphMy<TWeight>::inSourceSegment(int i)
{
assert(i >= 0 && i < (int)vtcs.size());
return vtcs[i].t == 0;
};
4. 源文件
main.cpp
#include <iostream>
#include "gcgraphMy.h"
#include "opencv2/opencv.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include<opencv2/imgproc/imgproc_c.h>
#include <iostream>
using namespace std;
using namespace cv;
/*
This section shows how to use the library to compute
a minimum cut on the following graph :
*/
///
#include <stdio.h>
const int nDownSample = 1;
const Scalar RED = Scalar(0, 0, 255);
const Scalar PINK = Scalar(230, 130, 255);
const Scalar BLUE = Scalar(255, 0, 0);
const Scalar LIGHTBLUE = Scalar(255, 255, 160);
const Scalar GREEN = Scalar(0, 255, 0);
#define MASK_BG_COLOR 128
#define MASK_FG_COLOR 255
const Scalar FG_MASK_COLOR = Scalar(255, 255, 255);
const Scalar BG_MASK_COLOR = Scalar(128, 128, 128);
const int BGD_KEY = EVENT_FLAG_CTRLKEY;
const int FGD_KEY = EVENT_FLAG_SHIFTKEY;
static void getBinMask(const Mat& comMask, Mat& binMask)
{
if (comMask.empty() || comMask.type() != CV_8UC1)
CV_Error(Error::StsBadArg, "comMask is empty or has incorrect type (not CV_8UC1)");
if (binMask.empty() || binMask.rows != comMask.rows || binMask.cols != comMask.cols)
binMask.create(comMask.size(), CV_8UC1);
binMask = comMask & 1;
}
static void showImageS2(const Mat& image, const string& winName)
{
resizeWindow(winName.c_str(), image.cols / nDownSample, image.rows / nDownSample);
imshow(winName, image);
}
class GCApplication
{
public:
enum{ NOT_SET = 0, IN_PROCESS = 1, SET = 2 };
static const int radius = 2;
static const int thickness = -1;
void reset();
void setImageAndWinName(const Mat& _image, const string& _winName);
void showImage(int x, int y, int FgPoint);
void mouseClick(int event, int x, int y, int flags, void* param);
void graphConstruct(const Mat& img, GCGraphMy<double>& graph);
void estimateSegmentation(GCGraphMy<double>& graph);
int nextIter();
int getIterCount() const { return iterCount; }
void calSeedPHist(const Mat& img, const Mat& mask);
private:
void setRectInMask();
void fillSeedToMask(Mat& mask);
void setLblsInMask(int x, int y, bool isFg);
double calFgdPrioriCost(Vec3b &color);
double calBgdPrioriCost(Vec3b &color);
const string* winName;
const Mat* image;
Mat mask;
Mat imgShowPg;
Mat bgdModel, fgdModel;
double FgPHist[3][256];
double BgPHist[3][256];
double gamma;
double lambda;
double beta;
Mat leftW, upleftW, upW, uprightW;
GCGraphMy<double> graphMy;
uchar rectState, lblsState, prLblsState;
bool isInitialized;
Rect rect;
vector<Point> fgdPxls, bgdPxls, prFgdPxls, prBgdPxls;
int iterCount;
};
void GCApplication::reset()
{
if (!mask.empty())
{
mask.setTo(Scalar::all(GC_BGD));
namedWindow("mask", 0);
}
bgdPxls.clear(); fgdPxls.clear();
prBgdPxls.clear(); prFgdPxls.clear();
this->image->copyTo(imgShowPg);
isInitialized = false;
rectState = NOT_SET;
lblsState = NOT_SET;
prLblsState = NOT_SET;
iterCount = 0;
}
void GCApplication::setImageAndWinName(const Mat& _image, const string& _winName)
{
if (_image.empty() || _winName.empty())
return;
image = &_image;
winName = &_winName;
mask.create(image->size(), CV_8UC1);
reset();
}
void GCApplication::showImage(int x, int y, int FgPoint)
{
static Point pre_pt = (-1, -1);//初始坐标
if (image->empty() || winName->empty())
return;
pre_pt = Point(x, y);
if (FgPoint == 1)
{
circle(imgShowPg, pre_pt, 3, BLUE, FILLED, CV_AA, 0);//划圆
circle(mask, pre_pt, 3, FG_MASK_COLOR, FILLED, CV_AA, 0);//划圆
}
else if (FgPoint == 2)
{
circle(imgShowPg, pre_pt, 3, GREEN, FILLED, CV_AA, 0);//划圆
circle(mask, pre_pt, 3, BG_MASK_COLOR, FILLED, CV_AA, 0);//划圆
}
showImageS2(imgShowPg, *(this->winName));
showImageS2(mask, "mask");
}
void GCApplication::setRectInMask()
{
assert(!mask.empty());
mask.setTo(GC_BGD);
rect.x = max(0, rect.x);
rect.y = max(0, rect.y);
rect.width = min(rect.width, image->cols - rect.x);
rect.height = min(rect.height, image->rows - rect.y);
(mask(rect)).setTo(Scalar(GC_PR_FGD));
}
void GCApplication::setLblsInMask(int x, int y, bool isFg)
{
vector<Point> *bgpxls, *fgpxls;
uchar bvalue, fvalue;
bgpxls = &bgdPxls;
fgpxls = &fgdPxls;
Point p(x, y);
//x,y就是原始图像中的,不需要上采样回去
//p.x = p.x * nDownSample;//上采样回去
//p.y = p.y * nDownSample;//上采样回去
if (isFg)
{
fgpxls->push_back(p);
}
else
{
bgpxls->push_back(p);
}
}
void GCApplication::mouseClick(int event, int x, int y, int flags, void*)
{
// TODO add bad args check
switch (event)
{
case EVENT_LBUTTONDOWN: // set rect or GC_BGD(GC_FGD) labels
{
setLblsInMask(x, y, 1);
showImage(x, y, 1);
lblsState = SET;
}
break;
case EVENT_RBUTTONDOWN: // set GC_PR_BGD(GC_PR_FGD) labels
{
setLblsInMask(x, y, 0);
showImage(x, y, 2);
prLblsState = SET;
}
break;
case EVENT_LBUTTONUP:
lblsState = NOT_SET;
break;
case EVENT_RBUTTONUP:
prLblsState = NOT_SET;
break;
case EVENT_MOUSEMOVE:
if (lblsState != NOT_SET && flags & EVENT_FLAG_LBUTTON)
{
setLblsInMask(x, y, 1);
showImage(x, y, 1);
}
else if (prLblsState != NOT_SET && flags & EVENT_FLAG_RBUTTON)
{
setLblsInMask(x, y, 0);
showImage(x, y, 2);
}
break;
default:
lblsState = NOT_SET;
prLblsState = NOT_SET;
break;
}
}
/*
Calculate beta - parameter of GrabCut algorithm.
beta = 1 / (2 * avg(sqr(|| color[i] - color[j] || )))
*/
static double calcBeta(const Mat& img)
{
double beta = 0;
for (int y = 0; y < img.rows; y++)
{
for (int x = 0; x < img.cols; x++)
{
Vec3d color = img.at<Vec3b>(y, x);
if (x>0) // left
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y, x - 1);
beta += diff.dot(diff);
}
if (y>0 && x>0) // upleft
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y - 1, x - 1);
beta += diff.dot(diff);
}
if (y>0) // up
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y - 1, x);
beta += diff.dot(diff);
}
if (y>0 && x<img.cols - 1) // upright
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y - 1, x + 1);
beta += diff.dot(diff);
}
}
}
if (beta <= std::numeric_limits<double>::epsilon())
beta = 0;
else
beta = 1.f / (2 * beta / (4 * img.cols*img.rows - 3 * img.cols - 3 * img.rows + 2));
return beta;
}
/*
Calculate weights of noterminal vertices of graph.
beta and gamma - parameters of GrabCut algorithm.
*/
static void calcNWeights(const Mat& img, Mat& leftW, Mat& upleftW, Mat& upW, Mat& uprightW, double beta, double gamma)
{
const double gammaDivSqrt2 = gamma / std::sqrt(2.0f);
leftW.create(img.rows, img.cols, CV_64FC1);
upleftW.create(img.rows, img.cols, CV_64FC1);
upW.create(img.rows, img.cols, CV_64FC1);
uprightW.create(img.rows, img.cols, CV_64FC1);
for (int y = 0; y < img.rows; y++)
{
for (int x = 0; x < img.cols; x++)
{
Vec3d color = img.at<Vec3b>(y, x);
if (x - 1 >= 0) // left
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y, x - 1);
leftW.at<double>(y, x) = gamma * exp(-beta*diff.dot(diff));
}
else
leftW.at<double>(y, x) = 0;
if (x - 1 >= 0 && y - 1 >= 0) // upleft
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y - 1, x - 1);
upleftW.at<double>(y, x) = gammaDivSqrt2 * exp(-beta*diff.dot(diff));
}
else
upleftW.at<double>(y, x) = 0;
if (y - 1 >= 0) // up
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y - 1, x);
upW.at<double>(y, x) = gamma * exp(-beta*diff.dot(diff));
}
else
upW.at<double>(y, x) = 0;
if (x + 1<img.cols && y - 1 >= 0) // upright
{
Vec3d diff = color - (Vec3d)img.at<Vec3b>(y - 1, x + 1);
uprightW.at<double>(y, x) = gammaDivSqrt2 * exp(-beta*diff.dot(diff));
}
else
uprightW.at<double>(y, x) = 0;
}
}
}
void GCApplication::calSeedPHist(const Mat& img, const Mat& mask)
{
int nFgNum = 0;//
int nBgNum = 0;//
memset(&FgPHist[0][0], 0, 256 * 3 * sizeof(double));
memset(&BgPHist[0][0], 0, 256 * 3 * sizeof(double));
Point p;
for (p.y = 0; p.y < img.rows; p.y++)
{
for (p.x = 0; p.x < img.cols; p.x++)
{
uchar pMaskV = mask.at<uchar>(p);
//背景像素值如直方图
if (MASK_BG_COLOR == pMaskV)
{
Vec3b color = img.at<Vec3b>(p);
nBgNum++;
BgPHist[0][color[0]]++;
BgPHist[1][color[1]]++;
BgPHist[2][color[2]]++;
}
//前景像素值如直方图
else if (MASK_FG_COLOR == pMaskV)
{
Vec3b color = img.at<Vec3b>(p);
nFgNum++;
FgPHist[0][color[0]]++;
FgPHist[1][color[1]]++;
FgPHist[2][color[2]]++;
}
}//
}//
nFgNum = nFgNum > 0 ? nFgNum : 1;//
nBgNum = nBgNum > 0 ? nBgNum : 1;//
//归一化并防止除0
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 256; j++)
{
FgPHist[i][j] = FgPHist[i][j] / nFgNum;
FgPHist[i][j] = FgPHist[i][j] < 0.00001 ? 0.00001 : FgPHist[i][j];
BgPHist[i][j] = BgPHist[i][j] / nBgNum;
BgPHist[i][j] = BgPHist[i][j] < 0.00001 ? 0.00001 : BgPHist[i][j];
}
}
}
double GCApplication::calFgdPrioriCost(Vec3b &color)
{
double p = FgPHist[0][color[0]] * FgPHist[1][color[1]] * FgPHist[2][color[2]];
return p;
}
double GCApplication::calBgdPrioriCost(Vec3b &color)
{
double p = BgPHist[0][color[0]] * BgPHist[1][color[1]] * BgPHist[2][color[2]];
return p;
}
void GCApplication::fillSeedToMask(Mat& mask)
{
Point p;
for (p.y = 0; p.y < mask.rows; p.y++)
{
for (p.x = 0; p.x < mask.cols; p.x++)
{
if (mask.at<uchar>(p) != MASK_BG_COLOR
&& mask.at<uchar>(p) != MASK_FG_COLOR)
{
mask.at<uchar>(p) = 0;
}
}//
}//
}
void GCApplication::graphConstruct(const Mat& img, GCGraphMy<double>& graph)
{
gamma = 50;
lambda = 1000;
beta = calcBeta(*(this->image));
Mat leftW, upleftW, upW, uprightW;
calcNWeights(img, leftW, upleftW, upW, uprightW, beta, gamma);
int vtxCount = img.cols*img.rows,
edgeCount = 2 * (4 * img.cols*img.rows - 3 * (img.cols + img.rows) + 2);
fillSeedToMask(this->mask);
calSeedPHist(img, this->mask);
graph.create(vtxCount, edgeCount);
Point p;
double a = 1.5;
for (p.y = 0; p.y < img.rows; p.y++)
{
for (p.x = 0; p.x < img.cols; p.x++)
{
// add node
int vtxIdx = graph.addVtx();
Vec3b color = img.at<Vec3b>(p);
// set t-weights
double fromSource, toSink;
if (mask.at<uchar>(p) == 0)
{
fromSource = -a*log(calBgdPrioriCost(color));
toSink = -a*log(calFgdPrioriCost(color));
}
else if (mask.at<uchar>(p) == MASK_BG_COLOR)
{
fromSource = 0;
toSink = lambda;
}
else if (mask.at<uchar>(p) == MASK_FG_COLOR) // GC_FGD
{
fromSource = lambda;
toSink = 0;
}
graph.addTermWeights(vtxIdx, fromSource, toSink);
// set n-weights,每个点只需要与左上4个点进行边连接即可,这样可以不重复的添加所有的N-8-edge
if (p.x>0)
{
double w = leftW.at<double>(p);
graph.addEdges(vtxIdx, vtxIdx - 1, w, w);
}
if (p.x>0 && p.y>0)
{
double w = upleftW.at<double>(p);
graph.addEdges(vtxIdx, vtxIdx - img.cols - 1, w, w);
}
if (p.y>0)
{
double w = upW.at<double>(p);
graph.addEdges(vtxIdx, vtxIdx - img.cols, w, w);
}
if (p.x<img.cols - 1 && p.y>0)
{
double w = uprightW.at<double>(p);
graph.addEdges(vtxIdx, vtxIdx - img.cols + 1, w, w);
}
}
}
}
/*
Estimate segmentation using MaxFlow algorithm
*/
void GCApplication::estimateSegmentation(GCGraphMy<double>& graph)
{
graph.maxFlow();
mask.setTo(GC_BGD);
Point p;
for (p.y = 0; p.y < mask.rows; p.y++)
{
for (p.x = 0; p.x < mask.cols; p.x++)
{
if (1 == graph.inSourceSegment(p.y*mask.cols + p.x /*vertex index*/))
{
mask.at<uchar>(p) = MASK_FG_COLOR;
}
}//
}//
showImageS2(mask, "mask");
waitKey();
destroyWindow("mask");
}
GCApplication gcapp;
static void on_mouse(int event, int x, int y, int flags, void* param)
{
gcapp.mouseClick(event, x, y, flags, param);
}
int main()
{
string filename = "E:/documents/vs2019/opencv-test/build/Debug/femur.png";//分割图像路径
Mat image = imread(filename, 1);
if (image.empty())
{
cout << "\n Durn, couldn't read image filename " << filename << endl;
return 1;
}
const string winName = "image";
//缩放图像,避免图像太大,界面无法显示,且分辨率大的图,对本方法没有帮助
resize(image, image, Size(image.cols / 3, image.rows / 3), 0, 0, INTER_LINEAR);
namedWindow(winName, 0);
resizeWindow(winName.c_str(), image.cols / nDownSample, image.rows / nDownSample);
gcapp.setImageAndWinName(image, winName);
setMouseCallback(winName, on_mouse, 0);
imshow(winName, image);
waitKey();
GCGraphMy <double>stGraphMy;
gcapp.graphConstruct(image, stGraphMy);
gcapp.estimateSegmentation(stGraphMy);
destroyWindow(winName);
//gcapp.setImageAndWinName(image, winName);
//gcapp.showImage();
system("pause");
return 0;
}
///
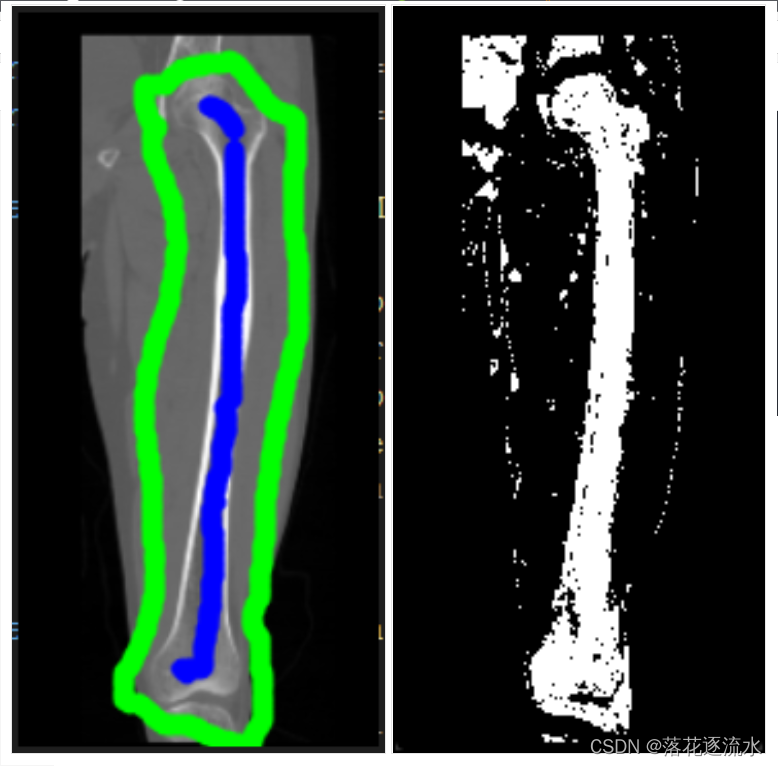
5. 测试图像
上述代码核心部分不是调用opencv实现的。
代码有冗余,是没有完成的Grabcut部分。可运行部分是GraphCut部分。
参考:经典图割算法中图的构建及实现:Graph-Cut