1 求梯度

sympy实际上提供了求梯度的方法，但个人认为不是很直观，求出的是$\frac{\partial f}{\partial x}\vec{i}+\frac{\partial f}{\partial y}\vec{j}+\frac{\partial f}{\partial z}\vec{k}$，并不是$[\frac{\partial f}{\partial x}\frac{\partial f}{\partial y}\frac{\partial f}{\partial z}{]}^T$。因此，这里采取了另一种方法，用求jacobi矩阵的方法间接得到梯度。实际上当$f(x,y,z)$是个标量时，求出的jacobi矩阵就是$[\frac{\partial f}{\partial x}\frac{\partial f}{\partial y}\frac{\partial f}{\partial z}]$，和梯度向量只差了一个转置。

import sympy as sym
x,y,z=sym.symbols('x y z')
f=sym.Matrix([x**2+sym.exp(y)+sym.log(z)])
gradient = f.jacobian([x,y,z]).T
print(gradient)

运行结果：

Matrix([[2*x], [exp(y)], [1/z]])

使用subs方法可以求出在某一点处的梯度：

print(gradient.subs([(x,1),(y,0),(z,1)])) #在x=1,y=0,z=1处的梯度值

运行结果：

Matrix([[2], [1], [1]])

2 求Hessian矩阵

from sympy import hessian
# 如果不导入hessian 就使用sympy.matrices.dense.hessian
x1,x2=sym.symbols('x1 x2')
f3=x1**2+sym.log(x2)
hessian(f3,(x1,x2)) 

运行结果:

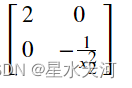
同样可以用subs方法求出某一点处的hessian矩阵，即${\nabla }^{2}f(x)$