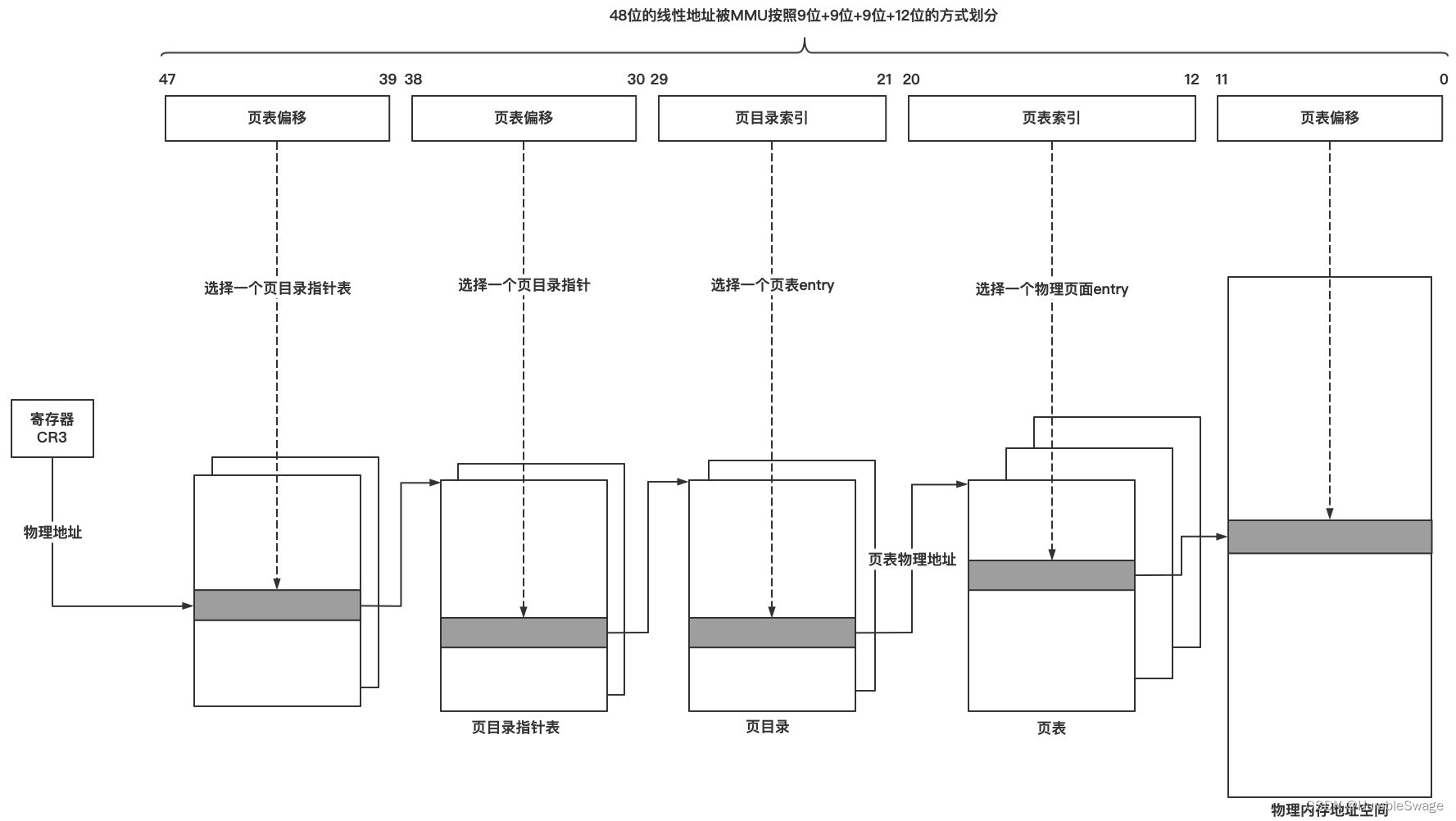
损失函数的作用为度量神经网络预测信息与期望信息(标签)的距离,预测信息越接近期望信息,损失函数值越小。
在目标检测领域,常见的损失分为分类损失和回归损失。
L1损失
L1 Loss也称为平均绝对值误差(MAE),是指模型预测值f(x)和真实值y之间绝对差值的平均值,公式如下:
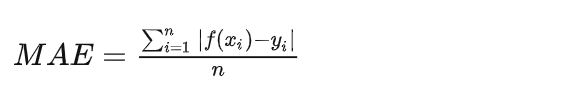
优点:
L1损失函数的导数是常量,有着稳定的梯度,所以不会有梯度爆炸的问题。
缺点:
在-1到1之间时,由于其梯度仍为1或-1,即梯度没有任何变换,而在该区间时,误差以及很小了,那么我们希望在该部分的梯度应该小一些,来慢慢逼近。
L2损失
L2 Loss也称为均方误差(MSE),是指模型预测值f(x)和真实值y之间差值平方的平均值,公式如下:
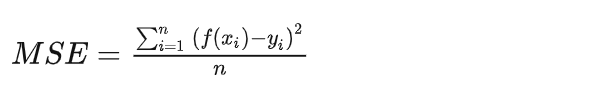
优点:
函数曲线连续,处处可导,随着误差值的减小,梯度也减小,有利于收敛到最小值。
缺点:
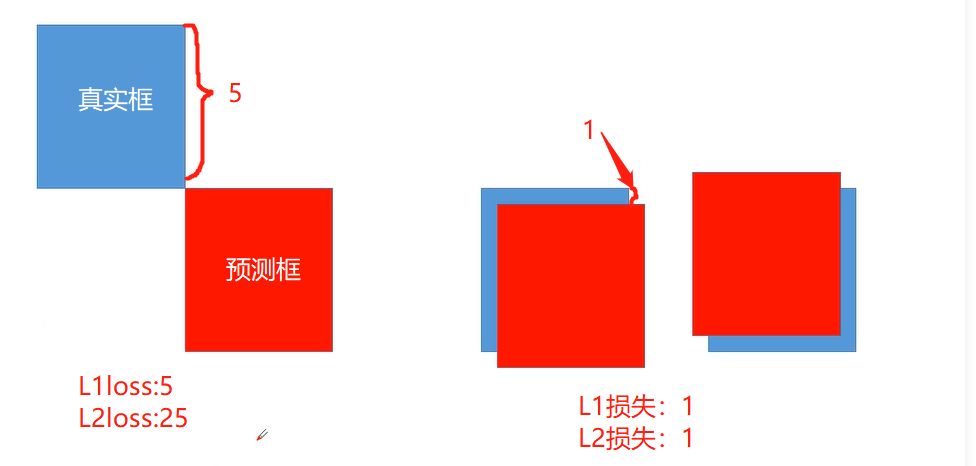
当误差较大时,由于其导数为2x,故此时期梯度较大,且对异常值十分敏感,即遇到异常值不够稳定(鲁棒性不强),如下图对异常值表现过于敏感。
综合考量,我们希望损失函数在误差较小时能够较为平滑的,缓慢的逼近,即梯度应该减小,而在误差较大时,希望其能够平稳,鲁棒性好,故提出了L1损失与L2损失的变种,Smooth L1。
Smooth L1损失
简单的说Smooth L1就是一个平滑版的L1 Loss,其公式如下:
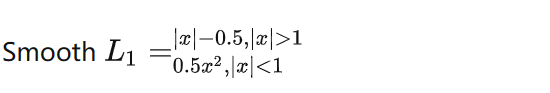
该函数实际上是一个分段函数,在[-1,1]之间就是L2损失,解决L1在0处有折点,在[-1, 1]区间以外就是L1损失,解决离群点梯度爆炸问题,所以能从以下两个方面限制梯度:
- 当预测值与真实值误差过大时,梯度值不至于过大;
- 当预测值与真实值误差很小时,梯度值足够小。
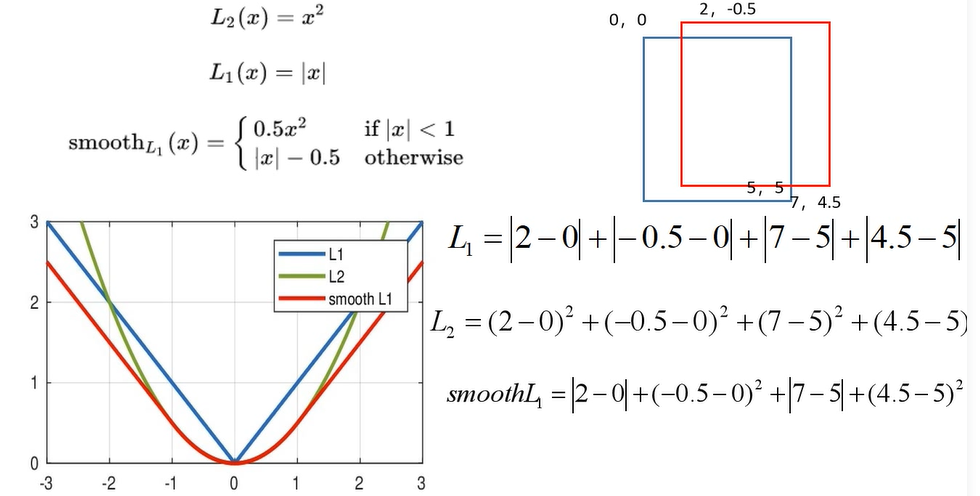
下图为三者综合:
IOU 损失
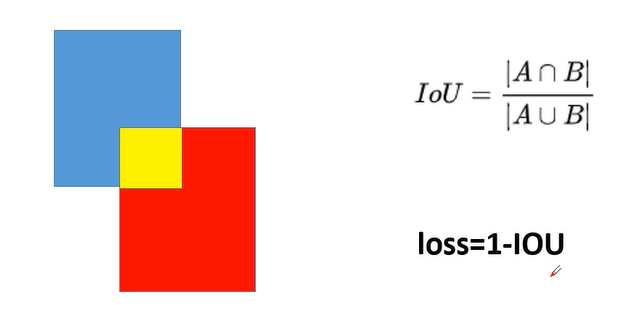
IoU就是我们所说的交并比,是目标检测中最常用的指标,在anchor-based的方法中,他的作用不仅用来确定正样本和负样本,还可以用来评价输出框(predict box)和ground-truth的距离。

优点:
可以说它可以反映预测检测框与真实检测框的检测效果。
还有一个很好的特性就是尺度不变性,也就是对尺度不敏感(scale invariant), 在regression任务中,判断predict box和gt的距离最直接的指标就是IoU。
缺点:
如果两个框没有相交,根据定义,IoU=0,不能反映两者的距离大小(重合度)。同时因为loss=0,没有梯度回传,无法进行学习训练。
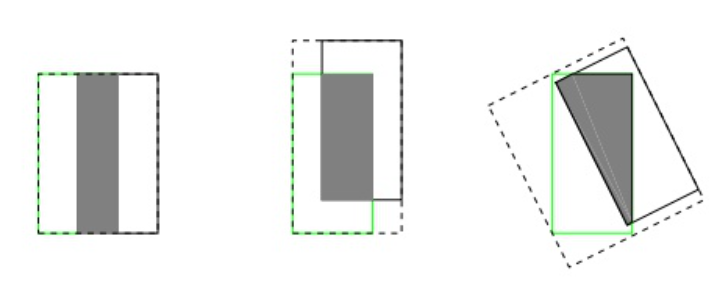
IoU无法精确的反映两者的重合度大小。如下图所示,三种情况IoU都相等,但看得出来他们的重合度是不一样的,左边的图回归的效果最好,右边的最差。
def box_iou_pairwise(boxes1, boxes2):
area1 = box_area(boxes1)
area2 = box_area(boxes2)
lt = torch.max(boxes1[:, :2], boxes2[:, :2]) # [N,2]
rb = torch.min(boxes1[:, 2:], boxes2[:, 2:]) # [N,2]
wh = (rb - lt).clamp(min=0) # [N,2]
inter = wh[:, 0] * wh[:, 1] # [N]
union = area1 + area2 - inter
iou = inter / union
return iou, union
GIOU损失
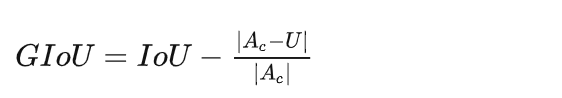
先计算两个框的最小闭包区域面积 Ac (通俗理解:同时包含了预测框和真实框的最小框的面积),再计算出IoU,再计算闭包区域中不属于两个框的区域占闭包区域的比重,最后用IoU减去这个比重得到GIoU。

优点:
缺点:
当
def generalized_box_iou(boxes1, boxes2):
"""
Generalized IoU from https://giou.stanford.edu/
The boxes should be in [x0, y0, x1, y1] format
Returns a [N, M] pairwise matrix, where N = len(boxes1)
and M = len(boxes2)
"""
# degenerate boxes gives inf / nan results
# so do an early check
assert (boxes1[:, 2:] >= boxes1[:, :2]).all()
assert (boxes2[:, 2:] >= boxes2[:, :2]).all()
iou, union = box_iou(boxes1, boxes2)
lt = torch.min(boxes1[:, None, :2], boxes2[:, :2])
rb = torch.max(boxes1[:, None, 2:], boxes2[:, 2:])
wh = (rb - lt).clamp(min=0) # [N,M,2]
area = wh[:, :, 0] * wh[:, :, 1]
return iou - (area - union) / (area + 1e-6)
DIOU损失
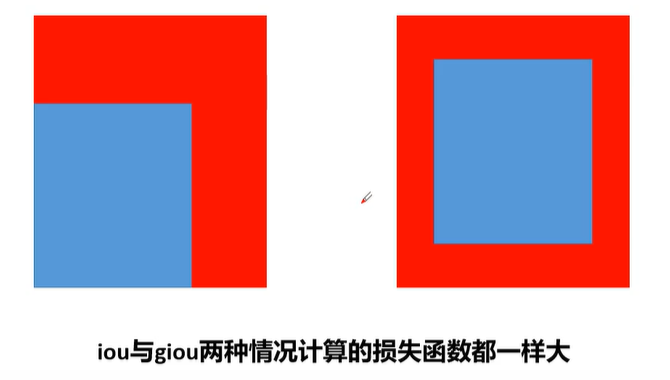
问题如下:此时iou与giou的损失一样大。此时的GIOU也退化为IOU
提出了DIOU
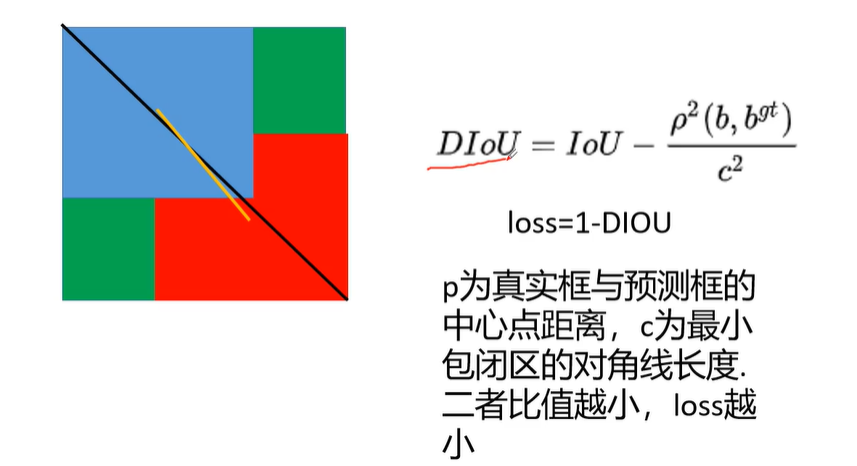
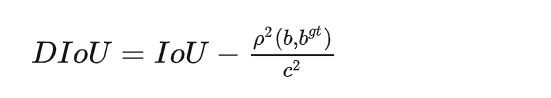
上述损失函数中,b,bgt分别代表了anchor框和目标框的中心点,且p代表的是计算两个中心点间的欧式距离。c代表的是能够同时覆盖anchor和目标框的最小矩形的对角线距离。
def Diou(bboxes1, bboxes2):
rows = bboxes1.shape[0]
cols = bboxes2.shape[0]
dious = torch.zeros((rows, cols))
if rows * cols == 0: #
return dious
exchange = False
if bboxes1.shape[0] > bboxes2.shape[0]:
bboxes1, bboxes2 = bboxes2, bboxes1
dious = torch.zeros((cols, rows))
exchange = True
# #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]
w1 = bboxes1[:, 2] - bboxes1[:, 0]
h1 = bboxes1[:, 3] - bboxes1[:, 1]
w2 = bboxes2[:, 2] - bboxes2[:, 0]
h2 = bboxes2[:, 3] - bboxes2[:, 1]
area1 = w1 * h1
area2 = w2 * h2
center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2
inter_max_xy = torch.min(bboxes1[:, 2:], bboxes2[:, 2:])
inter_min_xy = torch.max(bboxes1[:, :2], bboxes2[:, :2])
out_max_xy = torch.max(bboxes1[:, 2:], bboxes2[:, 2:])
out_min_xy = torch.min(bboxes1[:, :2], bboxes2[:, :2])
inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
inter_area = inter[:, 0] * inter[:, 1]
inter_diag = (center_x2 - center_x1) ** 2 + (center_y2 - center_y1) ** 2
outer = torch.clamp((out_max_xy - out_min_xy), min=0)
outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
union = area1 + area2 - inter_area
dious = inter_area / union - (inter_diag) / outer_diag
dious = torch.clamp(dious, min=-1.0, max=1.0)
if exchange:
dious = dious.T
return dious
CIOU损失
问题如下:由于没有考虑到长宽比例,其损失值相同
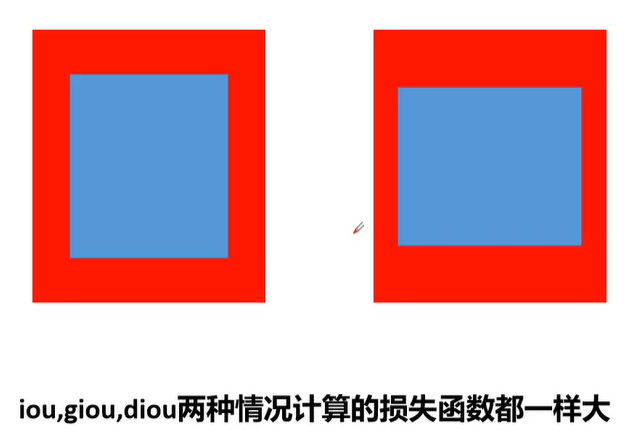
故而提出CIOU,CIOU引入了长宽比,即v,并在v前加了一个动态权重值a,其越大,说明更关注长宽比,而其要想变大,则iou应该较大。

其中v的求法中前面的常数项作为一个经验值。此外也可采用其他的函数而不使用arctan,其意图为当两者长宽比差距越小,那么损失值也就越小。
如下图中右图由于iou较小,我们肯定不会考虑长宽比,因为两图长宽比是相同的,那么此时a就应该越小,应该将重心放到如何使其宽高变大上,而在左图,其iou较大,即在大小上已经相似,那么我们就需要关注其长宽比,其注意到其形状。

def box_ciou(b1, b2):
"""
输入为:
----------
b1: tensor, shape=(batch, feat_w, feat_h, anchor_num, 4), xywh
b2: tensor, shape=(batch, feat_w, feat_h, anchor_num, 4), xywh
返回为:
-------
ciou: tensor, shape=(batch, feat_w, feat_h, anchor_num, 1)
"""
# 求出预测框左上角右下角
b1_xy = b1[..., :2]
b1_wh = b1[..., 2:4]
b1_wh_half = b1_wh / 2.
b1_mins = b1_xy - b1_wh_half
b1_maxes = b1_xy + b1_wh_half
# 求出真实框左上角右下角
b2_xy = b2[..., :2]
b2_wh = b2[..., 2:4]
b2_wh_half = b2_wh / 2.
b2_mins = b2_xy - b2_wh_half
b2_maxes = b2_xy + b2_wh_half
# 求真实框和预测框所有的iou
intersect_mins = torch.max(b1_mins, b2_mins)
intersect_maxes = torch.min(b1_maxes, b2_maxes)
intersect_wh = torch.max(intersect_maxes - intersect_mins, torch.zeros_like(intersect_maxes))
intersect_area = intersect_wh[..., 0] * intersect_wh[..., 1]
b1_area = b1_wh[..., 0] * b1_wh[..., 1]
b2_area = b2_wh[..., 0] * b2_wh[..., 1]
union_area = b1_area + b2_area - intersect_area
iou = intersect_area / torch.clamp(union_area, min=1e-6)
# 计算中心的差距
center_distance = torch.sum(torch.pow((b1_xy - b2_xy), 2), axis=-1)
# 找到包裹两个框的最小框的左上角和右下角
enclose_mins = torch.min(b1_mins, b2_mins)
enclose_maxes = torch.max(b1_maxes, b2_maxes)
enclose_wh = torch.max(enclose_maxes - enclose_mins, torch.zeros_like(intersect_maxes))
# 计算对角线距离
enclose_diagonal = torch.sum(torch.pow(enclose_wh, 2), axis=-1)
ciou = iou - 1.0 * (center_distance) / torch.clamp(enclose_diagonal, min=1e-6)
v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(b1_wh[..., 0] / torch.clamp(b1_wh[..., 1], min=1e-6)) - torch.atan(
b2_wh[..., 0] / torch.clamp(b2_wh[..., 1], min=1e-6))), 2)
alpha = v / torch.clamp((1.0 - iou + v), min=1e-6)
ciou = ciou - alpha * v
return ciou
阿尔法IOU

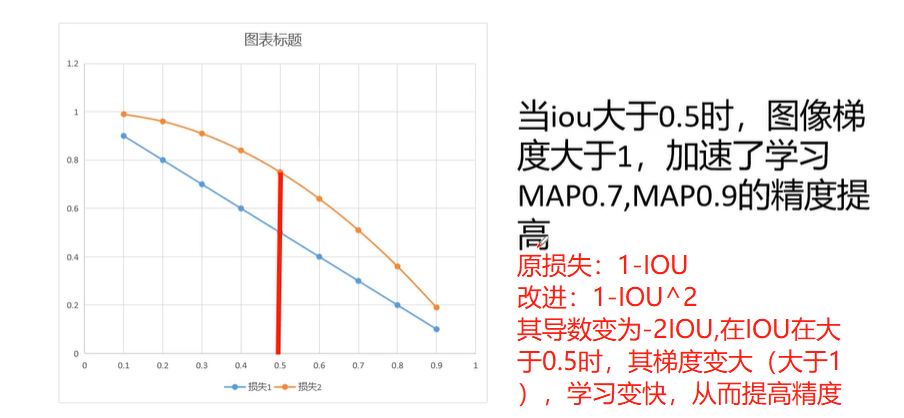
阿尔法IOU为何有用?
![[HNCTF 2022 WEEK4]ezheap](https://img-blog.csdnimg.cn/11be67eefbb646ef88bfb1bd38a8feec.png)