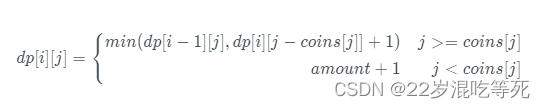首先是我对背包问题的理解：

        有一个背包可以放下 n kg，有一些物品，价值和重量一一对应，问题是，需要怎样才能使背包中的价值最大？

        不同的规则对应不同的背包问题

        01背包：每一个物品只能被放入一次

        完全背包：每个物品的放入数量不限

二维

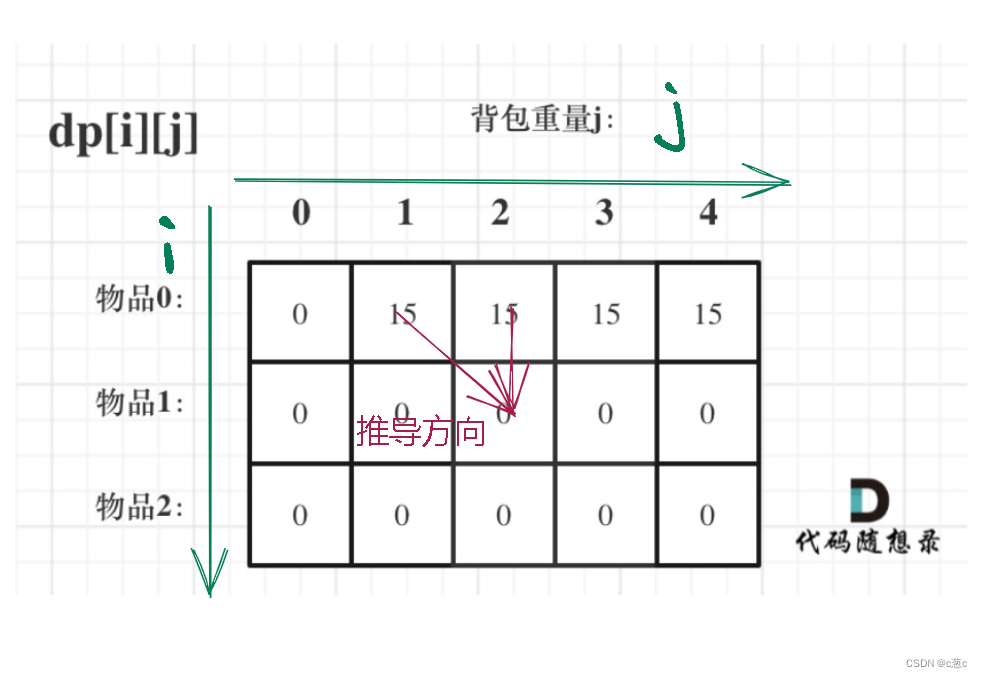
1.dp[ i ] [ j ] 数组的含义

        下标： i 表示  0 - i 的物品中可以任取   j 表示 背包的容量

        值：表示，此时背包中的最大值

2. 递推公式

        不放物品 i ：dp[ i ] [ j ]  = dp[ i  - 1 ] [ j ]  （也就是，和上一层的值是一样的

        放物品 i ： dp[ i ] [ j ] =  dp[ i  - 1 ] [ j  - weight[  i  ] ] + value[ i ] )

注意，这里将 最后写的时候 取二者的最大值

3. 初始化

        因为最后需要靠二维数组中 左边 和 上面 进行推导，所以需要初始化两个位置

        

 

for (int i = 0; i < weight.size(); i++)
    {
        dp[i][0] = 0;
    }

for (int j = 1; j <= bagweight; j++)
    {
        dp[0][j] = value[0];
    }

      

4. 遍历顺序

        两层for循环，先遍历物品再遍历背包  /   先遍历背包再遍历物品 都可以

        因为当前的值，是依靠左上  或者 上方的 值来的，和遍历顺序没有关系。

vector<int> weight = { 1, 3, 4 };
    vector<int> value = { 15, 20, 30 };
    int bagweight = 4;
    
    // 定义dp数组 
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
    
    // 初始化
    for (int i = 0; i < weight.size(); i++)
    {
        dp[i][0] = 0;
    }

    for (int j = 1; j <= bagweight; j++)
    {
        dp[0][j] = value[0];
    }
    
    // 遍历 + 递推
    for (int i = 1; i < weight.size(); i++)
    {
        for (int j = 0; j <= bagweight; j++)
        {
            if (j < weight[i]) dp[i][j] = dp[i - 1][j];
            else dp[i][j] = max(dp[i][j] = dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        } 
         
    }
    
    // 打印验证
    cout << dp[weight.size() - 1][bagweight] << endl;