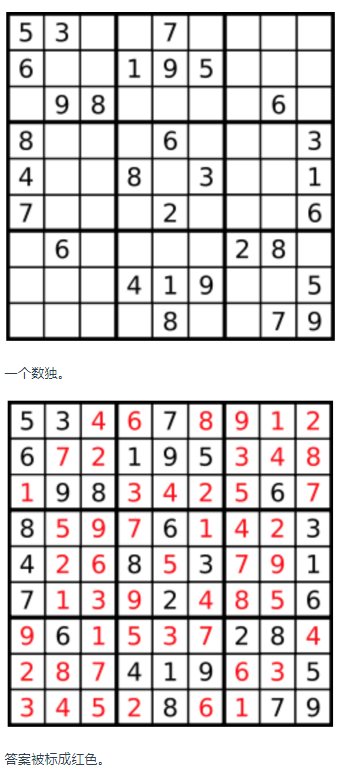
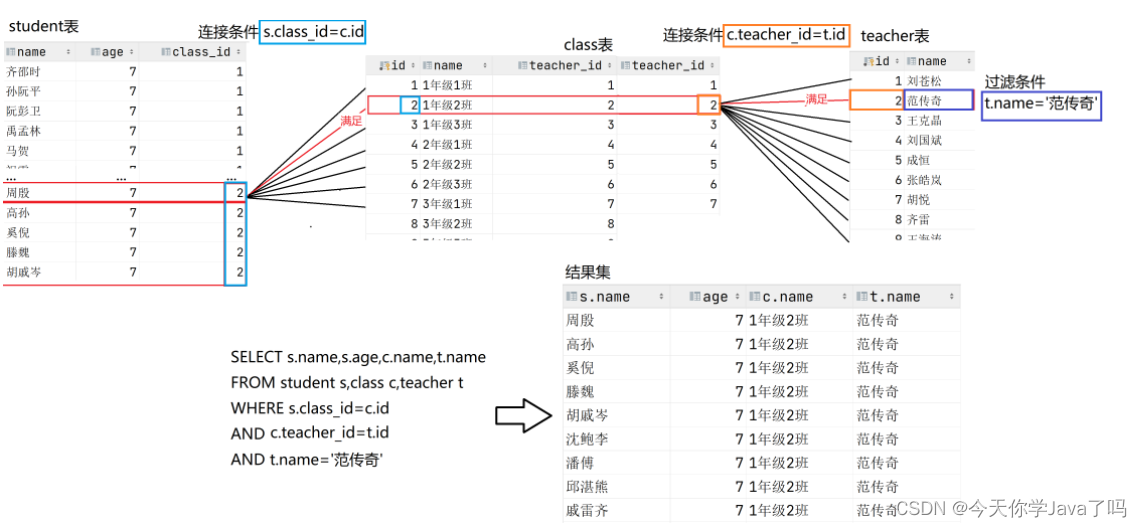
量表是一种测量工具，量表设计标准有很多，并且每种量表的设计都有各自的特性，不同量表的特性也决定了测量尺度，在数据分析中常用的量表为李克特量表。李克特量表1932年由美国社会心理学家李克特在当时原有总加量表的基础上进行改进而形成的，它是一种市场调查的方法，该表一般设置五种答案，记为1、2、3、4、5，另外还有七级量表等。

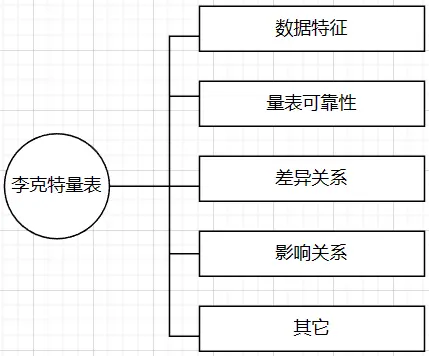
因为李克特量表比较常用，所以本篇文章以李克特量表（下文简称量表数据）的分析进行说明。一般可以分为六大部分，第一部分样本数据的特征描述，第二部分为量表可靠性，第三部分为差异关系，第四部分为影响关系，以及其它描述，接下来一一进行说明。

1. 数据特征
   当搜集完成样本数据后，首先进行数据特征的描述，目的在于更深入的了解样本的基本情况，比如统计描述分析或者频数分析等进一步了解样本人群的特征行为或者基本态度情况。
2. 量表可靠性
   量表可靠性可以通过信效度分析进行描述，什么是信度？信度简单来说就是研究样本数据是否真实可信。什么是效度？效度是说明问卷的测量项设计是否合理下面会具体说明。
3. 差异关系
   一般在进行量表可靠性研究后，如果研究者想要继续挖掘样本信息，得到更多有效的结论，常见的就是差异关系和相关以及影响关系，首先说明差异关系，差异关系比如研究不同性别对于产品满意度是否有差异，不同学历对于商场服务态度的满意度是否有差别，一般通常使用方差分析，t检验或者卡方检验进行研究，常常使用t检验或者方差分析比较多，三者区别在于数据类型有所不同，下面会具体描述。
4. 相关和影响关系
   除了研究差异关系还可以研究相关及影响关系，相关关系研究两个变量之间的关系，通过相关关系，研究人员可以大致清楚变量之间的基本关系如何以及是否有相关关系，一般研究相关关系大多是为了进行回归分析做铺垫，因为有相关关系不一定有影响关系，但是有影响关系一定有相关关系，所以一般研究者在进行回归分析前先进行相关关系的研究。
5. 其它

有时还会研究多个样本进行分类（聚类分析）或者进行指标的权重计算等等。接下来会进行说明。

一、数据特征

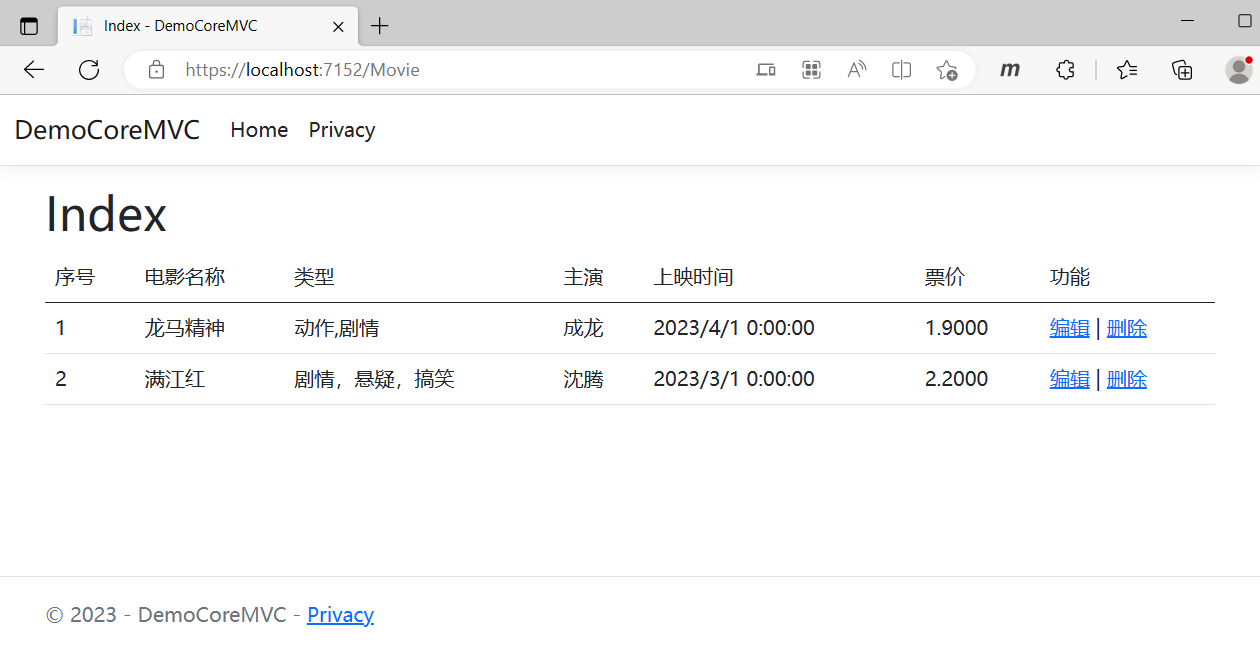
一般描述数据特征使用频数分析或者描述分析了解数据分布特征，有时为了更直观的表达结果也可以用可视化图形进行描述。案例背景：问卷主要研究员工满意度情况，员工满意度分为四个变量分别为个人发展、工作特性、领导管理和工作回报，四个维度下由2~4个量表题进行表示（文末有问卷数据可以粘贴到浏览器中进行使用）。比如想要研究被调查者“是否同意劳动付出与工作收入匹配这个观点”分析的结果如下：

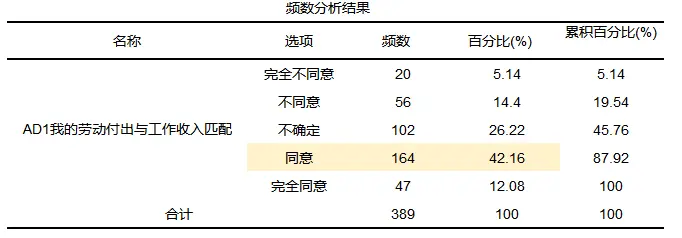
从表格结果可以得到共搜集389个有效样本，其中同意上述看法的人占比最大共有164人，并且持有“同意”和“完全同意”看法的人占比共为42.16％+12.08％=54.24％，所以说明超过一半的调查者同意“劳动付出与工作收入匹配”这个观点，与此同时量表题也可以和人口统计学进行交叉分析，比如分析不同性别、不同职业的观点或者看法等。接下来进行查看量表的可靠性。

二、量表可靠性

量表可靠性可以从信度和效度角度进行说明，信度分析即样本有没有真实回答了问题。通常情况下，信度分析仅仅只能分析量表题项。信度分析仅针对定量数据。
效度分析即研究测量题项设计是否合理。正常情况下，效度分析仅仅针对量表数据，非量表题目比如多选，单选性别之类的题目不能进行效度分析。如果一定想分析效度，建议可使用‘内容效度’，即用文字详细描述问卷设计的过程，用文字的形式描述清楚问卷是做什么，有什么用处，为什么合理，而且有专家认证，这样就说明问卷设计合理有效。一般来讲要先有信度再有效度，所以先进行信度分析。
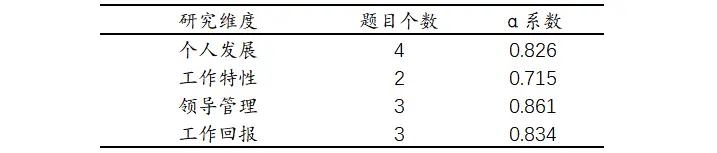
信度分为内在信度和外在信度，具体区别可以参考推荐文章（下述中有提供），这里对内在信度进行信度系数有多种计算，但是常用的就是克隆巴赫系数所以例子也以克隆巴赫系数进行说明。因为此问卷共包含4个维度所以分维度进行信度分析结果整理如下：

SPSSAU：关于信度分析的多种方法7 赞同 · 0 评论文章正在上传…重新上传取消

接下来查看问卷的效度，由于问卷量表共有四个维度所以维度个数设置为4。操作如下：

结果如下：

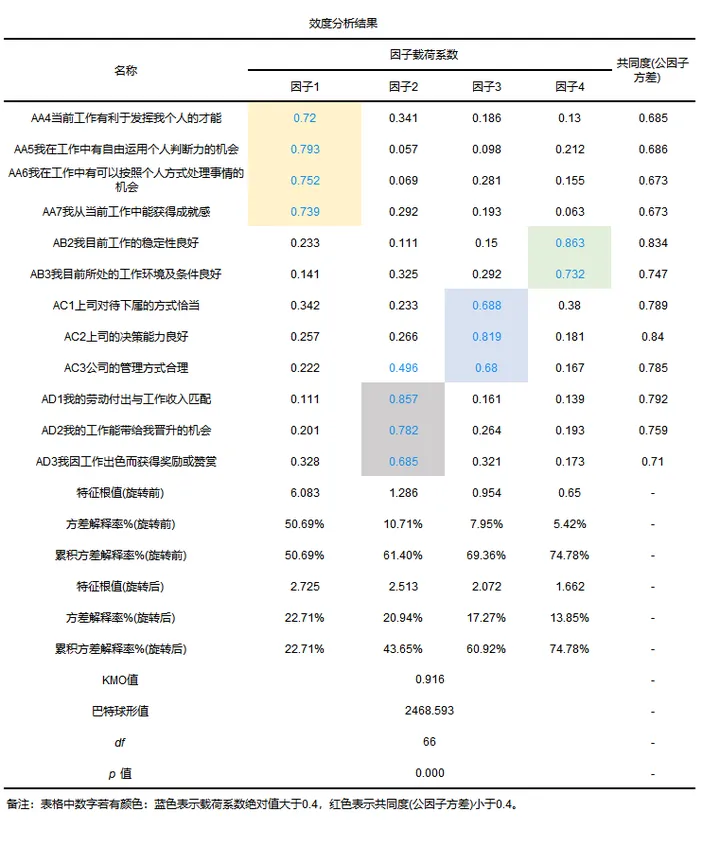
从上表可以看到效度分析12个量表题目共分为4个维度，从结果来看结构良好，并且从上表可知，KMO值为0.916>0.6，并且p值小于0.05通过巴特球形检验，累积方差解释率值为74.78%，说明4个维度可以提取出大部分题项信息。因而综合说明研究数据具有良好的结构效度水平。更多内容还可以参考：

SPSSAU：毕业论文中的问卷如何做效度分析？3 赞同 · 0 评论文章正在上传…重新上传取消

三、差异关系

差异关系一般用于比较两组或多组数据之间的差异。对于差异关系的研究常见的方法有t检验、方差以及卡方检验。三者的区别在于数据类型不同，t检验（这里值独立样本t检验）和方差（这里指单因素方差分析）要求数据自变量为定类变量，因变量为定量变量，卡方检验要求自变量与因变量均为定类变量，对于t检验和方差，如果自变量为两组比如男和女则一般使用t检验，如果自变量为两组以上比如“小学”、“初中”和“高中”，一般使用方差分析。比如想要研究问卷中“不同职位的个人发展是否有差别”，由于职位的组别为两组以上所以使用方差分析（单因素方差分析）进行描述，首先先将个人发展下的4个量表题合成一个变量。

步骤如下：

1. 首先点击【数据处理】中的【生成变量】；
2. 然后选择个人发展下的四个量表题
3. 因为是量表题合成一个维度，所以利用平均值进行处理
4. 最后将维度命名，点击确认处理

然后将以职位为自变量，个人发展为因变量做单因素方差分析，结果如下：

从结果中可以得到模型的F值为3.061，p值为0.028小于0.05所以模型显著，说明不同职位的个人发展有差异。同理还可以用独立样本t检验分析不同性别的个人发展是否有差异，结果如下：

从结果中也发现t值为-2.597，p值约为0.01<0.05，所以说明不同性别的人对个人发展有差异。更多内容可以参考：

SPSSAU：差异性分析该如何选择？4 赞同 · 2 评论文章正在上传…重新上传取消

四、相关及影响关系

处理研究差异关系，量表题还可以研究相关和影响关系，比如想要研究个人发展、工作特性以及领导管理对工作回报的影响关系，首先将多个量表题合成一个维度，步骤和上述一致，然后进行分析，得到结果如下：

因为研究个人发展、工作特性以及领导管理对工作回报的影响关系，数据都为定量变量所以使用线性回归进行分析，首先分析前对分析项进行相关关系检验，结果如下：

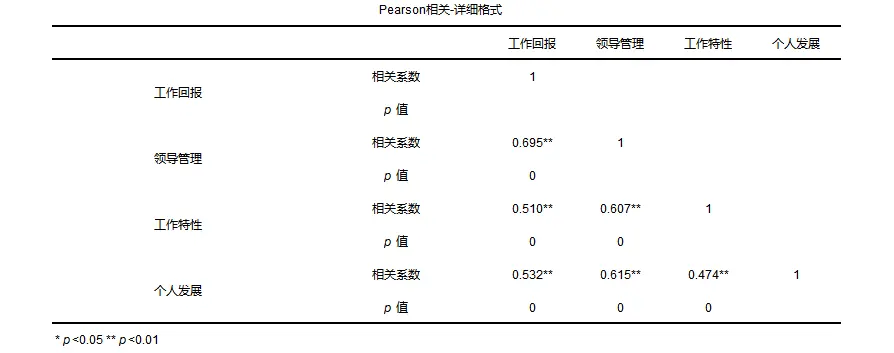
从上表格中看到，利用相关分析研究工作回报与领导管理、工作特性以及个人发展三项之间的相关关系，结果得知，工作回报与三者之间均存在相关关系，所以接下来进行回归分析：

首先查看F检验，结果如下：

上表格可以得出，回归平方和维149.909，残差平方和为144.613,总平方和为149.909+144.613=294.522，F统计量为133.033以及p值小于0.05所以说明模型构建有意义，至少有一个自变量对因变量产生影响。查看回归结果如下：

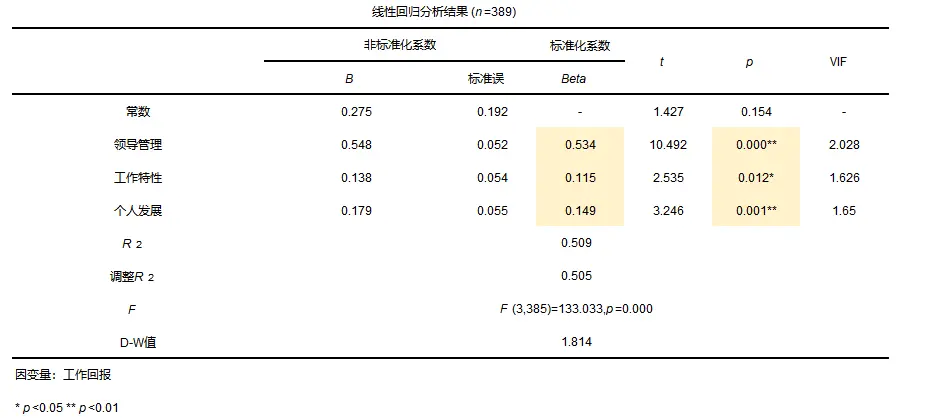
以工作回报为因变量，领导管理、工作特性、个人发展为自变量建立线性回归方程，从结果中得到，领导管理、工作特性、个人发展三个变量的p值均小于0.05，并且回归系数均大于0所以，领导管理、工作特性、个人发展均对工作回报产生正向的影响作用，因为只想研究影响关系所以对于回归方程的模型等不过多赘述