FIR半带滤波器
半带滤波器原理:
CIC滤波器是一种适合于工作在高采样率条件下的滤波器。
半带滤波器是一种非常适合于2倍抽取的FIR滤波器。
半带滤波器可以使2倍抽取的每秒乘法次数比一般线性相位的FIR滤波器减少近1/2。
半带滤波器是一种实现数字下变频的高效数字滤波器。
半带滤波器的特点
半带滤波器有以下特点:1、滤波器的通带和阻带对称,即通带容限和阻带容限相等。
2、滤波器的系数具有偶对称特性,且滤波器长度为偶数(滤波器阶数为奇数)。
滤波器所有的大于0的偶数序号的冲击响应值均为0。
半带滤波器的这一特性大大降低了滤波器运算所需的乘法及加法次数。
3、经半带滤波器滤波后,进行2倍抽取时,信号通带内没有频谱混叠,但阻带内有频谱混叠。
半带滤波器的MATLAB设计
% 利用Matlab提供的firhalfband函数设计阶数为16、
% 通阻带容限为0.0001的半带滤波器。
% 仿真测试滤波前后的信号时域图,绘制滤波器的频率响应特性图。
%
% E6_10_HalfFilterMatlab.m
% 定义参数
f = 1000; %信号频率为 1kHz
Fs = 40*f; %采样频率为40kHz
n = 16; %半带滤波器阶数
D = 2; %抽取因子
dev = 0.0001; %通阻带容限
% % 产生正弦波信号
t = 0:1/Fs:0.02;
c = 2*pi*f*t;
si = sin(c);
% 设计半带滤波器
b = firhalfband(n,dev,'dev')%;
% disp(b);
s = filter(b,1,si); %对信号进行滤波处理
s = s/max(abs(si)); %归一化处理
Ds = s(1:D:length(t)); %对滤波后信号进行抽取
% 绘图
figure(1);
x = 0:1:100;
x = x/Fs;
Dx = x(1:D:length(x));
subplot(211);
stem(x,si(1:length(x))); %绘制离散序列数据
title('Matlab 仿真滤波前信号时域波形');
subplot(212);
stem(Dx,Ds(1:length(Dx)));
title('Matlab 仿真滤波后信号时域波形');
figure(2);
freqz(b);

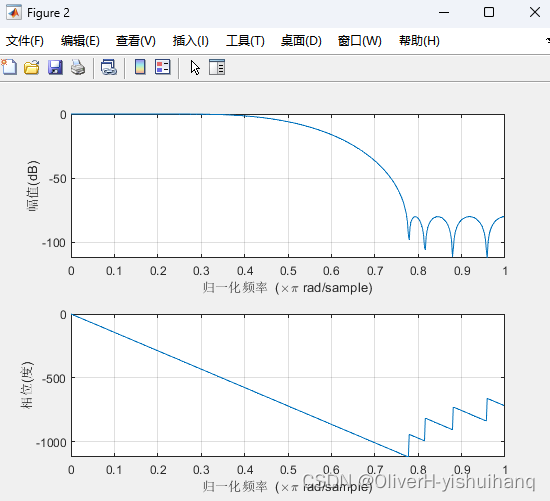
从运行结果可以看出,半带滤波器的系数有近一半为0,且呈偶对称特性。
从滤波前后信号的时域图、滤波器的频率响应图可以看出,经半带滤波器滤波后的信号,与原信号相比,波形没有改变,但抽样速率降低了一半;半带滤波器通阻带容限相同,具有严格的线性相位特性。