时序预测 | MATLAB实现WOA-GRU鲸鱼算法优化门控循环单元时间序列预测

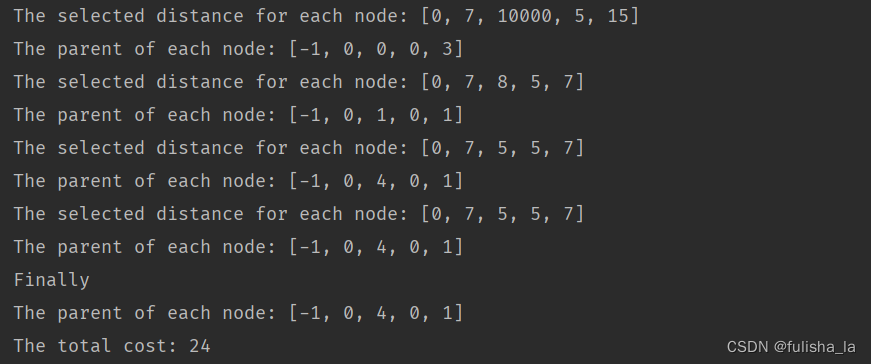
预测效果

基本介绍

MATLAB实现WOA-GRU鲸鱼算法优化门控循环单元时间序列预测
基于鲸鱼算法优化门控循环单元(WOA-GRU)的时间序列预测。
优化参数为学习率，隐藏层节点个数，正则化参数，要求2020b及以上版本，matlab代码。
评价指标包括:MAE、MSE、RMSE等，代码质量极高，方便学习和替换数据。

程序设计

• 完整程序和数据下载方式1(资源处直接下载)：MATLAB实现WOA-GRU鲸鱼算法优化门控循环单元时间序列预测
• 完整程序和数据下载方式2(订阅《GRU门控循环单元》专栏，同时可阅读《GRU门控循环单元》专栏收录的所有内容，数据订阅后私信我获取)：MATLAB实现WOA-GRU鲸鱼算法优化门控循环单元时间序列预测
• 完整程序和数据下载方式3(订阅《智能学习》专栏，同时获取《智能学习》专栏收录程序6份，数据订阅后私信我获取)：MATLAB实现WOA-GRU鲸鱼算法优化门控循环单元时间序列预测

% 预设鲸鱼优化算法的参数 
popsize = 5; %种群数量
maxgen = 20;  % WOA最大的迭代次数
dim = 3; % 优化的自变量个数 ，依次为GRU的第一和第二隐含层节点数，最大训练代数，初始学习率

   %输入输出数据
    L = size(output, 1); %样本总数
    %     testNumber = round(L*0.2); %设置四个样本测试
    testNumber =20; %设置四个样本测试
    trainNumber = L - testNumber; %训练样本数量
 
    % 划分训练集和测试集
    p_train = input(1:trainNumber, :)';
    t_train = output(1:trainNumber, :)';
    % 测试集 
    p_test = input(trainNumber+1:trainNumber+testNumber,:)';
    t_test = output(trainNumber+1:trainNumber+testNumber,:)';
        %% 归一化和元胞数组处理
    [pn_train ,ps]= mapminmax(p_train);
    [tn_train, ts] = mapminmax(t_train);
    %测试集的归一化
    pn_test = mapminmax('apply', p_test, ps);
    tn_test = mapminmax('apply', t_test, ts);

     for i = 1:length(t_train)
        P_train{i,1} =  pn_train(:,i);
    end
    for i = 1:length(t_test)
        P_test{i,1} =  pn_test(:,i);
    end

    %% 归一化和元胞数组处理p 4; % 优化的自变量个数 ，依次为GRU的第一和第二隐含层节点数，最大训练代数，初始学习率
    lb = [1, 1, 0.001]; % 下限
    ub = [10,20, 0.01]; % 上限

    % initialize position vector and score for the leader，初始化位置向量和领导者得分
    Leader_pos=zeros(1,dim);
    Leader_score=inf; %change this to -inf for maximization problems，将此更改为-inf以获得最大化问题，Inf无穷大


    %Initialize the positions of search agents
    Positions=initialization(popsize,dim,ub,lb);%Positions，存放数个个体的多维位置。

    Convergence_curve=zeros(1,maxgen);%Convergence_curve收敛曲线

    t=1;% Loop counter

    % Main loop
    while t<maxgen+1   % 首先  迭代次数的while循环   为2  也就是鲸鱼群体会进化2代

        disp(['current iteration is: ', num2str(t)])
        

        for i=1:size(Positions,1)%对每个个体一个一个检查是否越界  % 种群规模是2  所以嵌套了2次训练

            % Return back the search agents that go beyond the boundaries of
            % the search space，返回超出搜索空间边界的搜索代理
            Flag4ub=Positions(i,:)>ub;
            Flag4lb=Positions(i,:)<lb;
            Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;%超过最大值的设置成最大值，超过最小值的设置成最小值


            % 评估个体适应度，会调用func.m子函数，把个体位置坐标赋给GRU参数中，执行的训练
            % Calculate objective function for each search agent，目标函数值的计算
            [fitness,net]=func(Positions(i,:),p_train,P_train,P_test, tn_train,ts,t_train,t_test);
            if fitness<Leader_score % Change this to > for maximization problem
                Leader_score=fitness; % Update alpha
                Leader_pos=Positions(i,:);
                net1 = net;
            end

        end
        a=2-t*((2)/maxgen); % a decreases linearly fron 2 to 0 in Eq. (2.3)
        % a2 linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)，有疑问？
        a2=-1+t*((-1)/maxgen);

        % Update the Position of search agents，参数更新
        for i=1:size(Positions,1)
            r1=rand(); % r1 is a random number in [0,1]
            r2=rand(); % r2 is a random number in [0,1]

            A=2*a*r1-a;  % Eq. (2.3) in the paper 
            C=2*r2;      % Eq. (2.4) in the paper

            b=1;               %  parameters in Eq. (2.5)
            l=(a2-1)*rand+1;   %  parameters in Eq. (2.5)

            p = rand();        % p in Eq. (2.6)
            for j=1:size(Positions,2)%对每一个个体地多维度进行循环运算

                if p<0.5%收缩包围机制

参考资料

[1] https://blog.csdn.net/article/details/126072792?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/article/details/126044265?spm=1001.2014.3001.5502
[3] https://blog.csdn.net/article/details/126043107?spm=1001.2014.3001.5502