文章目录
- HOG+SVM分类器实践
- 制作SVM分类器
- 导入所需的库
- 提取HOG特征
- 读取正样本和负样本
- 训练分类器
- 定义主函数
- 小结
- 测试SVM分类器
- 相关疑问
- 1. 提取HOG特征为什么不能彩色图像呢?
- 2. 出现如下错误
- 3. 测试代码中,当我传入100*100的图片时候,为什么img_feature.shape是4356呢?
- 4. 减去的2和//8是什么意思?
- 5. 当输入图片是16*16时,print(img_feature.shape)是36,这个36是怎么获得的
HOG+SVM分类器实践
目标检测是计算机视觉领域的一个重要任务,目的是从给定的图像中找出感兴趣的目标,并标出它们的位置和类别。传统机器学习方法在目标检测中应用广泛,其中一种常见的方法是基于HOG特征和SVM分类器的方法。在下面的示例中,我们将使用Python编写代码来实现一个SVM分类器。
这个程序是用来训练一个基于HOG特征的SVM分类器,以区分正样本和负样本。具体来说,它从指定目录中读取正负样本图像,提取它们的HOG特征并将其作为训练数据,然后利用线性支持向量机(LinearSVC)算法来训练分类器,最后将分类器保存到文件中。可以调用分类器来检测其他图片。
这个代码是为了训练SVM分类器,以将正样本和负样本进行分类。它使用了一种基于HOG特征的方法来提取图像的特征,从而训练SVM分类器进行分类。它可以用于检测样本是否属于某一类别,但不能直接用于目标检测任务。要进行目标检测,通常需要使用滑动窗口和其他技巧来在图像中搜索可能包含目标的区域,然后对这些区域进行分类。
制作SVM分类器
导入所需的库
首先,我们需要导入所需的库,包括NumPy、OpenCV和Scikit-learn:
import numpy as np
import cv2
from sklearn.svm import LinearSVC
from skimage.feature import hog
提取HOG特征
接下来,我们定义一个函数来提取图像的HOG特征。这个函数使用Scikit-learn库中的hog函数来计算HOG特征。它的输入是一个图像,它的输出是一个向量,表示该图像的HOG特征:
def get_hog_features(img, orient, pix_per_cell, cell_per_block, vis=False, feature_vec=True):
"""
获取图像的HOG特征向量
:param img: 输入图像
:param orient: HOG特征的方向数
:param pix_per_cell: 细胞的像素数
:param cell_per_block: 每个块的细胞数
:param vis: 是否返回可视化HOG图像
:param feature_vec: 是否返回HOG特征向量
:return: HOG特征向量或可视化HOG图像
"""
# 检查vis参数是否为True,如果是,则返回特征向量和可视化HOG图像
if vis == True:
features, hog_image = hog(img, orientations=orient,
pixels_per_cell=(pix_per_cell, pix_per_cell),
cells_per_block=(cell_per_block, cell_per_block),
block_norm='L2-Hys', visualize=vis, transform_sqrt=True,
feature_vector=feature_vec)
return features, hog_image
# 如果vis参数不是True,只返回特征向量
else:
features = hog(img, orientations=orient,
pixels_per_cell=(pix_per_cell, pix_per_cell),
cells_per_block=(cell_per_block, cell_per_block),
block_norm='L2-Hys', visualize=vis, transform_sqrt=True,
feature_vector=feature_vec)
return features
另外,由于在函数注释部分使用了冒号和空格来分隔不同部分,这些注释会被识别为函数的 docstring,可以通过函数名后面的 .__doc__ 来调用该注释。例如,可以通过 print(get_hog_features.__doc__) 来输出函数的注释信息。
读取正样本和负样本
接下来,我们定义一个函数来从给定的目录中读取图像,提取它们的HOG特征,并将它们存储为训练数据。这个函数使用OpenCV库来读取图像,然后使用之前定义的get_hog_features函数来提取图像的HOG特征。它还将标注的对象的类别存储为训练数据的标签:
数据集文件夹如下配置
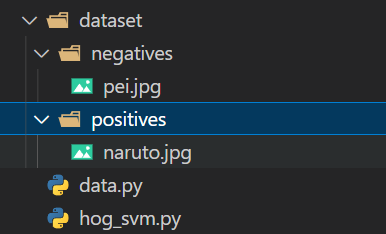
我就用了两个图片,一个正样本,一个负样本。正样本我采用的是鸣人,负样本我用的是佩恩。
切忌:你的数据集图片大小尺寸要是一致的,否则可能会出问题。


def get_data():
"""
从指定目录中读取图像,提取HOG特征,存储为训练数据
:return: 训练数据和标签
"""
# 定义正样本图像目录和负样本图像目录
pos_dir = 'dataset/positives' # 正样本图像目录
neg_dir = 'dataset/negatives' # 负样本图像目录
# 通过列表推导式获取正负样本图像的文件路径
pos_imgs = [os.path.join(pos_dir, f) for f in os.listdir(pos_dir) if os.path.isfile(os.path.join(pos_dir, f))]
neg_imgs = [os.path.join(neg_dir, f) for f in os.listdir(neg_dir) if os.path.isfile(os.path.join(neg_dir, f))]
# 提取正样本图像的HOG特征和HOG图像
pos_features = [] # 存放正样本图像的HOG特征
pos_hog_img = [] # 存放正样本图像的HOG图像
for img_path in pos_imgs:
img = cv2.imread(img_path, 0) # 以灰度图像读入图像文件
features, hog_img = get_hog_features(img, orient=9, pix_per_cell=8, cell_per_block=2, vis=True)
# 调用函数获取HOG特征和HOG图像
pos_features.append(features)
pos_hog_img.append(hog_img) # 存放可视化HOG图像
#------通过下面这行代码可以查看你训练集的可视化HOG图像,你图像比较少可以用
#------你图像比较多,建议注释下面两行,因为你需要一张一张的关闭掉图像,挺费劲的
plt.imshow(pos_hog_img[0], cmap='gray') # 可视化HOG图像
plt.show()
pos_labels = np.ones(len(pos_features)) # 正样本的标签为1(表示含有目标)
# 提取负样本图像的HOG特征和HOG图像
neg_features = [] # 存放负样本图像的HOG特征
neg_hog_img = [] # 存放负样本图像的HOG图像
for img_path in neg_imgs:
img = cv2.imread(img_path, 0) # 以灰度图像读入图像文件
features, neg_hog = get_hog_features(img, orient=9, pix_per_cell=8, cell_per_block=2, vis=True)
# 调用函数获取HOG特征和HOG图像
neg_features.append(features)
neg_hog_img.append(neg_hog) # 存放可视化HOG图像
plt.imshow(neg_hog_img[0]) # 可视化HOG图像
plt.show()
neg_labels = np.zeros(len(neg_features)) # 负样本的标签为0(表示不含目标)
# 将正样本和负样本的特征和标签组合成训练数据
features = np.vstack((pos_features, neg_features)) # 将正负样本的HOG特征按行堆叠
labels = np.hstack((pos_labels, neg_labels)) # 将正负样本的标签按行堆叠
print(labels.shape) # 输出标签数组的形状
return features, labels # 返回训练数据的特征和标签
训练分类器
现在,我们有了训练数据,我们可以使用Scikit-learn库中的LinearSVC来训练SVM分类器。我们定义一个函数来训练分类器,并将其保存到文件中以备后续使用:
def train_classifier(features, labels):
"""
训练SVM分类器并将其保存到文件中
:param features: 训练数据
:param labels: 训练标签
:return: None
"""
clf = LinearSVC()
clf.fit(features, labels)
#------保存为svm_classifier.pkl分类器,你可以通过调用这个分类器检测其他图片--------------#
joblib.dump(clf, 'svm_classifier.pkl')
定义主函数
现在,我们可以将这些函数组合起来并使用它们来训练我们的目标检测器。我们定义一个main函数来执行所有这些步骤:
import os
import joblib
def main():
# 获取训练数据
features, labels = get_data()
# 训练分类器
train_classifier(features, labels)
if __name__ == '__main__':
main()
小结
在这个示例中,我们展示了如何使用HOG特征和SVM分类器来训练一个简单的目标分类器,可以分辨鸣人和佩恩。它提供了一个基本的框架,可以用来训练一个自己的目标分类器。
---------------------------------------备注------------------------------------------------
精度很低,玩一玩是可以的。
测试SVM分类器
import cv2
import numpy as np
import joblib
from skimage.feature import hog
def predict(img_path, clf_path='svm_classifier.pkl'):
# 加载分类器
clf = joblib.load(clf_path)
# 提取测试图片的HOG特征
img = cv2.imread(img_path, 0) # 读取灰度图像
img_feature = hog(img, orientations=9, pixels_per_cell=(8, 8), cells_per_block=(2, 2),
block_norm='L2-Hys', transform_sqrt=True, feature_vector=True)
print(img_feature.shape)
# 进行预测
pred = clf.predict(np.array([img_feature]))
# 展示图片
cv2.imshow('image', img)
cv2.waitKey(0)
cv2.destroyAllWindows()
return pred[0]
def main():
# img_path = 'dataset/negatives/pei.jpg'
#-------------------------这里修改图片的路径名称---------------
img_path = 'test.jpg'
result = predict(img_path, 'svm_classifier.pkl')
if result == 0:
print('This is a negative image.')
else:
print('This is a positive image.')
if __name__ == '__main__':
main()
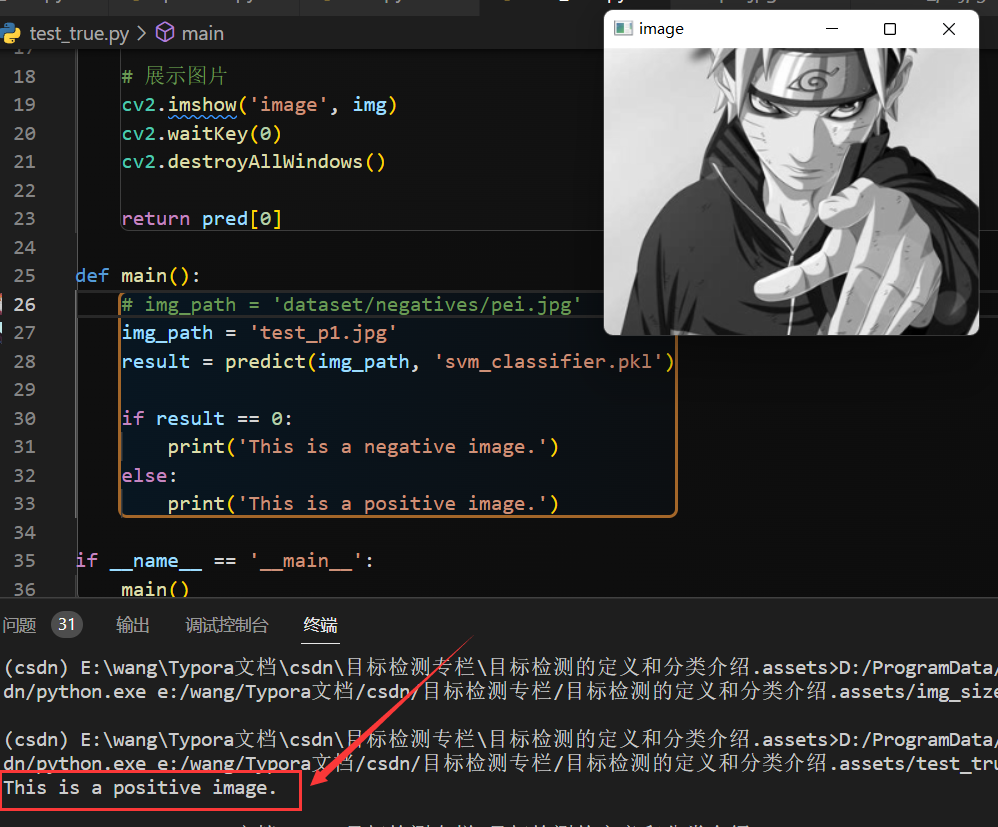
运行上述测试代码,可以看到输出测试的鸣人图片,并且在终端输出了 This is a positive image 。
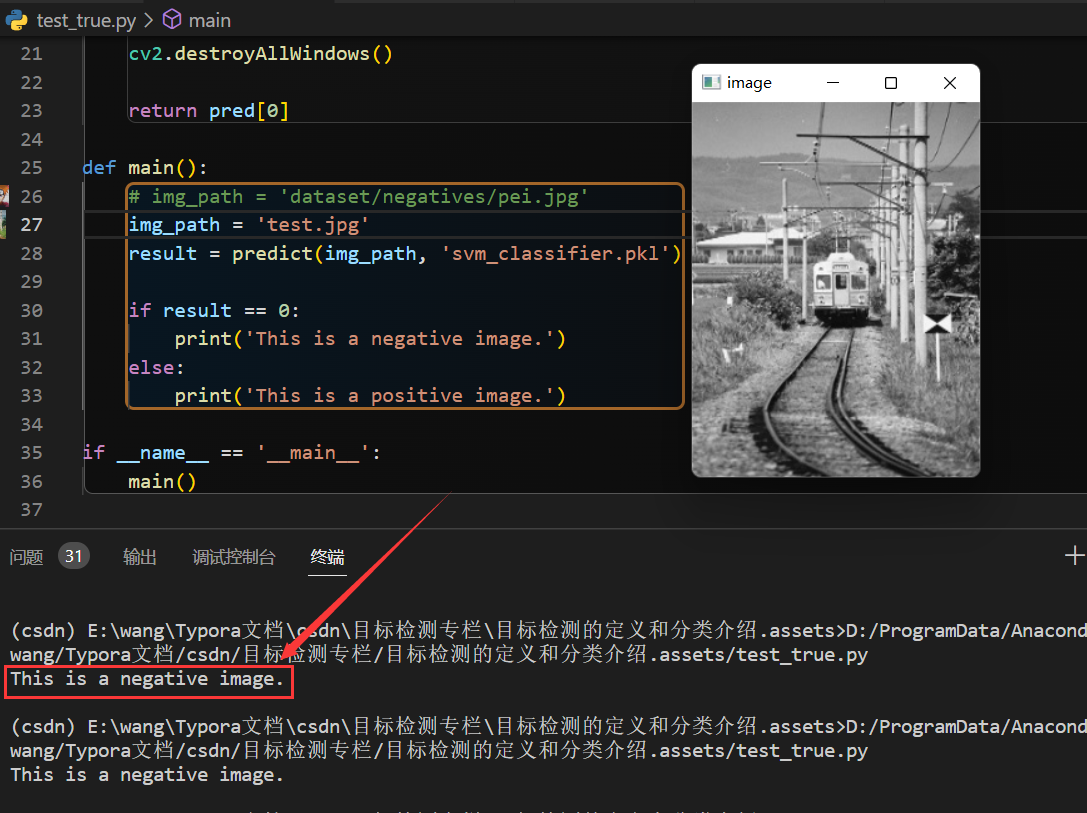
用一个火车的图片,可以看到输出是 This is a negative image
但是啊,误检测很严重,因为就用了一个正样本和负样本学习,分类器能力肯定不行的。你即使选择佩恩的图片,或者其他人物图片,他也会认为是真图片的。
这个不能称为目标检测。因为现在大家认为的目标检测,都会在原图片上把目标用矩形框框起来,而这个只能称作简单的分类器,它把待检测的图片预测成1或0,分辨物体是不是真图片或假图片。
相关疑问
训练的时候是灰度图像,因此测试的时候需要用灰度图像测试,如果直接用彩色图像测试会导致通道错误。
1. 提取HOG特征为什么不能彩色图像呢?
对于HOG算法来说,其最初目的是用于在灰度图像上检测边缘和方向,为了保留图像在块和细胞级别上的更丰富的边缘方向特征,输入图像需要是灰度图像。在彩色图像上直接使用HOG算法可能会导致HOG特征提取的结果不理想,因为彩色图像中的RGB或其他色彩通道的变化可能会干扰算法的表现,从而降低分类器的准确性。另外,彩色图像的通道数是3,如果直接使用彩色图像,则提取的特征向量维数将大于灰度图像的特征向量维数,这可能会增加算法的复杂性,导致需要更高的计算成本。因此,在实际中通常将输入图像转换为灰度图像进行HOG特征提取。
2. 出现如下错误

如果出现该错误,表明图像大小不一样。比如你用 256 ∗ 256 256*256 256∗256的图片训练,那么你测试的图片也需要 256 ∗ 256 256*256 256∗256。
3. 测试代码中,当我传入100*100的图片时候,为什么img_feature.shape是4356呢?

在该代码中,通过使用HOG算法对输入的灰度图像进行特征提取。在这个特定的函数中,通过使用hog()函数,并给定了以下参数来计算HOG特征:
- orientations=9 # 方向直方图数量
- pixels_per_cell=(8, 8) # 每个细胞的像素大小
- cells_per_block=(2, 2) # 每个块包含的细胞数
- block_norm=‘L2-Hys’ # 块规范化方法
- transform_sqrt=True # 对数据缩放开方,以获得更好的动态范围
- feature_vector=True # HOG特征向量
这些参数决定了hog()函数如何对图像进行处理,并获得特征向量。根据这些参数,将图像划分为多个大小为(8,8)的单元格(每个单元格具有64个像素),形成所谓的“cell”。 对每个单元格,计算直方图梯度,每个直方图包含了所涉及单元格中每个像素的幅值,方向,之后将它们放入“block”,这里每个块包含4个细胞。最终,使用块规范化来协调每个块的输出,确保输出的特征向量有更好的动态范围。
根据上述参数,图像的尺寸为100 x 100,划分为8 x 8的单元格时,每个细胞包含8 x 8个像素,每个块包含2 x 2个细胞,其中每个细胞对应一个方向梯度直方图,共9个bins。因此,每个单元格的方向梯度直方图包含9个定向的bin,一个块包含4个单元格,因此一个块的方向梯度直方图特征向量的长度为 9×4=36。 对于该代码给出的图像,形成的特征向量为大小为 (9-2) * ((100 // 8)-2) * 4 * 9 = 4356,减去的2和//8是因为目标图像的尺寸不足以提供块周围的两个单元格的信息。因此,包含4356个元素的一维特征向量被用作SVM分类器的输入。
4. 减去的2和//8是什么意思?
因为该代码中设置的cells_per_block为2 x 2,这意味着一个块由2 x 2个单元格组成。然而,在对图像进行“块”提取时,HOG算法需要在图像周围保留至少一个单元格以计算外部梯度。因此,在计算特征向量时,HOG算法需要丢弃图像周围的两个(上下、左右)单元格。 对于这个具体的函数,图像的尺寸为100 x 100,因此在使用8 x 8的单元格大小的情况下,可以形成12 x 12的单元格。然而,对于形状为12 x 12的单元格块,不能在图像的边缘提取其他块,因为图像的尺寸不足以在边缘形成2 x 2的单元格块。因此,需要在图像周围排除两个单元格边缘,即在高度和宽度上的2 x (8 // 8) =2 x 1 = 2个单元格。这就是代码中减去2的原因,并使用整除运算符//用于除以单元格的大小来计算需要从图像边缘删除的单元格数量。
在HOG算法中,图像被划分为多个单元格,每个单元格包含一组像素。而在这个特定的函数中,每个单元格的大小被设置为8 x 8像素。因此,如果输入图像的尺寸为100 x 100,那么图像可以被划分为12 x 12个单元格,其中每个单元格的大小为8 x 8像素。每个单元格的HOG特征向量都是通过计算其方向梯度直方图获得的,然后将这些特征拼接成一个特征向量。因此,在这个特定的函数中,通过这种方式处理图像,呈现的特征向量的长度是定的,即生成了由4356个元素组成的一维特征向量。
5. 当输入图片是16*16时,print(img_feature.shape)是36,这个36是怎么获得的
如果输入图像大小为 16 x 16,则该函数提取HOG特征向量的过程如下:
- 定义单元格大小
pixels_per_cell=(8, 8),每个单元格的大小为8 x 8;
2.定义块的大小 cells_per_block=(2, 2),每个块包含 2 x 2 个单元格;
- 因为该图像中只有
2 x 2个单元格,所以只有一个块,因此生成的 HOG 特征向量只有一个块的特征,即一个长度为 36 的一维向量。
对于每个单元格:
4.计算每个单元格内像素的梯度大小和梯度方向,并将其分配到其最接近的方向bin中;
- 构建每个单元格的梯度方向直方图,该直方图中包含9个方向bin,分别表示0°至180°之间的均匀间隔;
对于每个块:
cell=(8, 8),每个单元格的大小为 8 x 8`;
2.定义块的大小 cells_per_block=(2, 2),每个块包含 2 x 2 个单元格;
- 因为该图像中只有
2 x 2个单元格,所以只有一个块,因此生成的 HOG 特征向量只有一个块的特征,即一个长度为 36 的一维向量。
对于每个单元格:
4.计算每个单元格内像素的梯度大小和梯度方向,并将其分配到其最接近的方向bin中;
- 构建每个单元格的梯度方向直方图,该直方图中包含9个方向bin,分别表示0°至180°之间的均匀间隔;
对于每个块:
- 将每个块内包含的4个单元格的HOG特征向量拼接起来,形成一个块的HOG特征向量。