一、模态分解算法===============EMD算法介绍

（一）模态分解相关的算法有以下几类

IMF 固有模态函数\EMD经验模态分解\EEMD集合经验模态分解\CEEMD 互补集合经验\（EEMD的标准形式）CEEMDAN自适应噪声完备集合经验模态分解\VMD 变分模态分解

（二）本篇主要介绍EMD算法

IMF的定义：将待研究的信号分解为一个个单分量信号，每一个单分量信号只包含一种振荡模式（即单一的瞬时频率），这些分解后的分量称为固有模态函数

满足两点要求

1）极值点和过零点的数目应该相等，或者最多差一个

2）局部最大和局部最小的上下包络线均值为零

这两点要求是必要非充分条件，也就是IMF一定满足上面两个条件，但是满足上面两个条件的不一定是IMF。

（三）EMD的步骤

1）对信号x(t)，找出局部最大值和局部最小值点

2）再利用三次样条函数分别对这些局部最大值和局部最小值点进行插值得到x(t)的上包络线u(t)和下包络线l(t),获取上下包络线的均值

m(t) = [u(t)+l(t)]/2，则m(t)为上下包络线的均值。

3）令h(t) = x(t)-m(t);检查h(t)是否满足IMF的条件，如果不满足，则继续上述迭代过程至到某h(t)符合IMF的条件

以某心电数据为例，展示EMD的效果图：

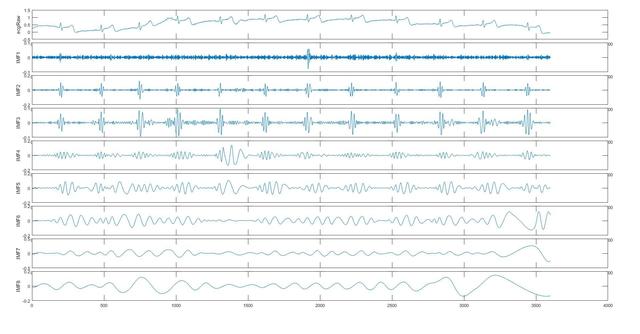
（四）EMD存在的问题

模式混合/模态混叠

1）一个单独的IMF信号中含有不同的时间尺度；

2）相同时间尺度出现在不同的IMF中。

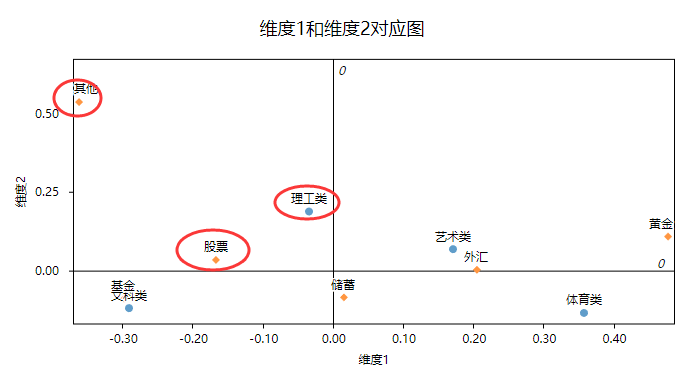
matlab论坛上面有一幅图可以清楚地展现这两个问题

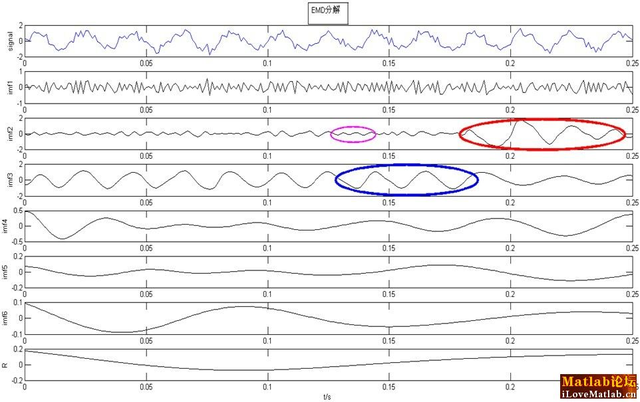
如上图所示，IMF2中存在两种模式，IMF2红色圈和MIF3蓝色圈中类似于一种模式。

我们在看EMD算法时，经常能够看到说单一模态、单一模式或者单一时间尺度，那么，单一模态，或者单一时间尺度的标准是什么？

1）信号中局部两个连续过零点之间的时间宽度一致

2）信号中两个连续峰值之间的时间宽度一致

3）曲率上两个连续峰值之间的时间宽度一致

为了解决EMD模式混叠的问题，学者们提出将正态分布的白噪声加到原始信号，于是EEMD分解算法产生了。

二、模态分解算法===============EEMD算法介绍

上面介绍了EMD算法，并分析了EMD算法的存在的问题，即分解后的IMF可能存在模式混叠。一旦IMF存在模式混叠，也就是IMF不是单一频率的分量，也就无法准确获取瞬时频率。为了解决这个问题，集合经验模态分解算法(EEMD)被提出。

（1）EEMD算法步骤如下：

1.将正态分布的白噪声加到原始信号；

2.将加入白噪声的信号作为一个整体，然后进行EMD分解，得到各IMF分量；

3.重复步骤1和2,每次加入新的正态分布白噪声序列；

4.将每次得到的IMF做集成平均处理后作为最终结果。

语言是苍白是，我们用图表示，如下：

集合经验模态分解算法流程

我们同样采样Matlab论坛里面的一张图

从上图可以看出，EMD存在的频谱混叠现象，而EEMD已经不存在。

（2）EEMD存在的问题

EEMD虽然解决了EMD出现的模式混叠问题，但是由于加入白噪声，因此也带来其他问题

1.集总平均后的IMF可能不再符合IMF的要求（偏差一般较小，不影响瞬时频率的计算）

2.集总平均次数一般在几百次以上，非常耗时；

3.白噪声在集总平均之后基本抵消，但存在残留，重建之后噪声不可忽略；

为了解决重建之后白噪声无法完全抵消，加和之后噪声过大的问题，CEEMD紧接着被提出。

三、模态分解算法===============CEEMD算法介绍

文章模态分解算法「一」EMD算法介绍介绍了EMD算法的流程，并分析了EMD算法存在的问题，即模式混叠，基于EMD存在的问题，文章模态分解算法「二」EEMD算法介绍介绍了在简单的EMD分解的基础上添加白噪声，从而使得分解的IMF是单一模式，优化了模式混叠，但是引入新的问题，即白噪声在集总平均之后不能完全抵消，而存在残留，导致重建之后的噪声不可忽略。因此互补集合经验模态CEEMD被提出。

CEEMD和EEMD流程相似，不同的是EEMD每次仅添加白噪声，CEEMD算法是将原信号加上白噪声和原信号减去白噪声两个信号同时经过EMD，求均值，用于抵消信号中加入的噪声。具体的算法流程如下所示：

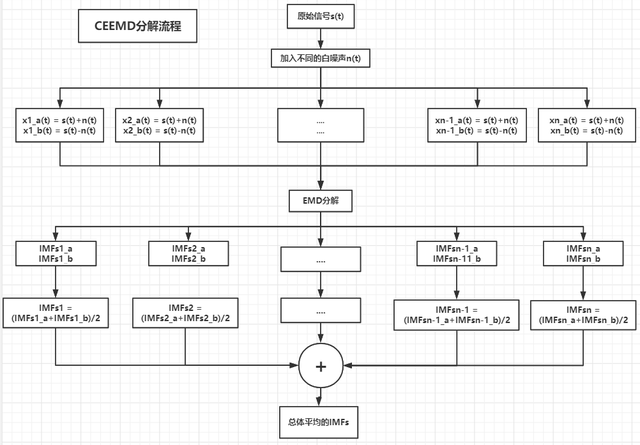
互补集合经验模态分解

s(t)为原始信号，加入不同的白噪声，共加入n次，也就是集总平均次数为n。分别对加噪声和减噪声的信号做EMD分解，将分解之后的两组IMF求均值，再将n组IMF求平均值，即可获得最终的IMF组分量。

CEEMD是对EEMD的优化，集总平均次数会减少，从EEMD的百量级减小到CEEMD的几十的量级，重建后的信号噪声明显减少。通常情况，集总平均次数越多，重构后的信号噪声越小。

说明&致谢：

本文仅供学习参考之用，参考及致谢：XieHS