7.1 贝叶斯决策论

贝叶斯决策论是概率框架下实施决策的基本方法。
假设有N种可能的类别标记，即y={c1,c2,…,cn}，λij是将一个真实标记为cj的样本误分类为ci所产生的损失。基于后验概率P(ci | x)可获得将样本x分类为ci所产生的期望损失，即在样本x上的条件风险：

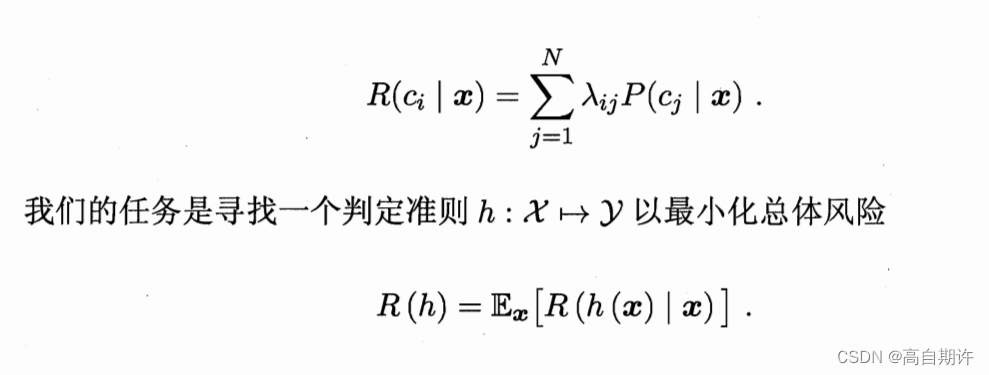
显然，对每个样本x，若h能最小化条件风险R(h(x)|x)，则总体风险R(h)也将被最小化。
这就产生了贝叶斯判定准则：为最小化总体风险，只需在每个样本上选择那个能使条件风险R(c|x)最小的类别标记，即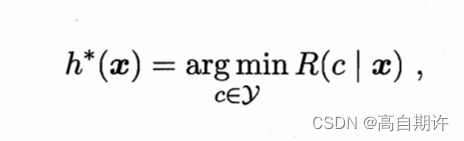
此时，h称为贝叶斯最优分类器，与之对应的总体风险R(h)称为贝叶斯风险。1-R(h*)反映了分类器所能达到的最好性能，即通过机器学习所能产生的模型精度的理论上限。
具体来说：若目标是最小化分类错误率，则误判损失λij可写为：

后验概率P(c|x),然而，在现实任务中这通常难以直接获得。机器学习所要实现的是基于有限的训练样本集尽可能准确地估计出后验概率P(c|x)。
大体来说，主要有两种策略：
1、给定x,可通过直接建模P(c|x)来预测c，这样得到地是判别式模型。
2、也可先对联合概率分布P(x,c)建模，然后再由此获得P(c|x)，这样得到地是生成式模型。
之前的决策树、BP神经网络、支持向量机、都可归入判别式模型的范畴。
对于生成式模型：

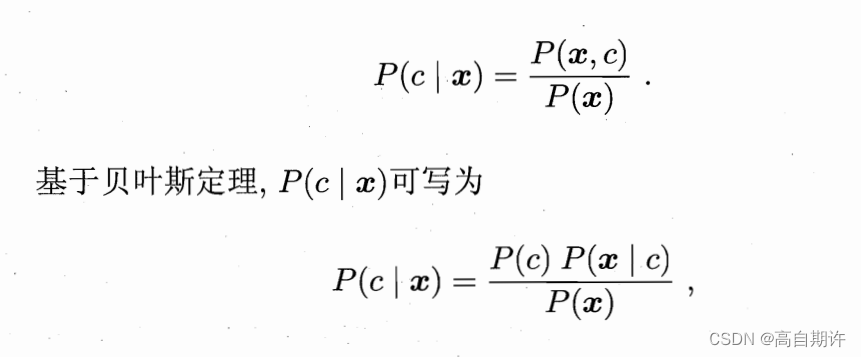
P©是类先验概率；
P(x|c)是样本x相对于类标记c的类条件概率，或称似然;
P(x)是用于归一化的证据因子。
证据因子与类标记无关，因此估计P(c|x)的问题就转化为如何基于训练数据D来估计先验P©和似然P(x|c)。

7.2 极大似然估计

估计类条件概率的一种常用策略是先假定其具有某种确定的概率分布形式，再基于训练样本对概率分布的参数进行估计。
事实上、概率模型的训练过程就是参数估计过程。
对于参数估计，统计学界的两个学派分别提供了不同的解决方案：
频率主义学派认为参数虽然未知，但却是客观存在的固定值，因此，可通过优化似然函数等准则来确定参数值。
贝叶斯学派则认为参数是未观察到的随机变量，其本身也可有分布，因此，可假定参数服从一个先验分布，然后基于观测到的数据来计算参数的后验分布。

极大似然估计（Maximum Likelihood Estimation，简称MLE）这是根据数据采样来估计概率分布参数的经典方法。


需注意的是，这种参数化的方法虽能使类条件概率估计变得相对简单，但估计结果的准确性严重依赖于所假设的概率分布形式是否符合潜在的真实数据分布。
现实应用中，欲做出能较好地接近潜在真实分布地假设，往往需在一定程度上利用关于应用任务本身的经验知识，否则若仅凭猜测来假设概率分布形式，很可能产生误导性的结果。

7.3 朴素贝叶斯分类器

不难发现，基于贝叶斯公式来估计后验概率主要困难在于：类条件概率是所有属性上的联合分布，难以从有限的训练样本直接估计而得。
为了避开上述障碍，朴素贝叶斯分类器采用了属性条件独立性假设：对已知类别，假设所有属性相互独立。
为了避免其他属性携带的信息被训练集中未出现的属性值抹去，在估计概率值时通常要进行平滑，常用“拉普拉斯修正”。显然拉普拉斯修正避免了因训练集样本不充分而导致概率估值为0的问题。并且在训练集变大时，修正过程所引入的先验的影响也会逐渐变得可忽略，使得估值渐趋向于实际概率值。

7.4半朴素贝叶斯分类器

为了降低贝叶斯公式中估计后验概率P(c|x)的困难，朴素贝叶斯分类器采用了属性条件独立性假设，但在现实任务中这个假设往往很难成立。于是，人们尝试对属性条件独立性假设进行一定程度的放松，由此产生了一类称为半朴素贝叶斯分类器的学习方法。
半朴素贝叶斯分类器的基本想法是适当考虑一部分属性间的相互依赖信息，从而既不需进行完全联合概率计算，又不至于彻底忽略了比较强的属性依赖关系。独依赖估计（One-Dependent Estimator classifiers）是半朴素贝叶斯分类器最常用的一种策略。顾名思义，所谓独依赖就是假设每个属性在类别之外最多仅依赖于一个其他属性。
最直接的做法是假设所有属性都依赖于同一个属性，称为超父，然后通过交叉验证等模型选择方法来确定超父属性。由此形成了SPODE(Super-Parent ODE)方法。下图中，x1就是超父属性

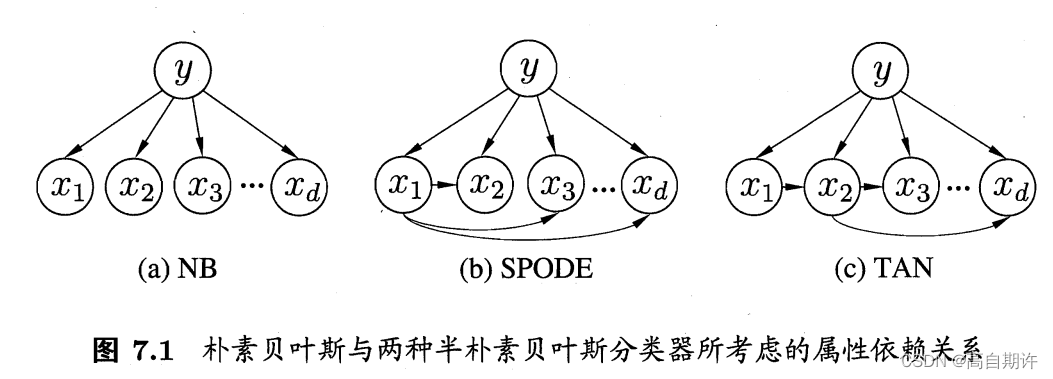
TAN（Tree Augmented naive Bayes）则是在最大带权生成树算法的基础上，通过以下步骤将属性间依赖关系简为上图中的树形结构。

容易看出，条件互信息I(xi,xj|y)刻画了属性xi与xj在已知类别情况下的相关性，因此、通过最大生成树算法，TAN实际上仅保留了强相关属性之间的依赖性。
AODE（Averaged One-Dependent Estimator）是一种基于集成学习机制，更为强大的独依赖分类器。与SPODE通过模型选择确定父属性不同，AODE尝试将每个属性作为超父来构建SPODE，然后将那些具有足够训练数据支撑的SPODE集成起来作为最终结果。
与朴素贝叶斯分类器类似，AODE的训练过程也是计数，即在训练数据集上对符合条件的样本进行计数的过程。与朴素贝叶斯分类器相似，AODE无需模型选择，既能通过预计算节省预测时间，也能采取懒惰学习方式在预测时再进行计数，并且易于实现增量学习。